一、二进制运算
二进制使用 0和 1来表示的数,二进制的基数为 2。二进制数据也采用位置计数法,权位是以 2为底的幂。
用 B表示二进制
进位规则:逢一进二;借位规则:借一当二
(一)二进制减法
例如计算 1001001 - 0101101=11100(73 - 45=28)运算过程,从右向左逐位运算:
1-1 = 0;
0-0 = 0;
0-1,0不够减 1,向前借一位后 +2 变成 2,得到 2-1 = 1;
1-1,1在上一步中被借 一所以就变成了 0,0不够减 1,向前借一位后加 2变成了2,得到 2-1=1;
0-0,0 在上一步被借一所以就变成了 -1,-1不够减 0,向前借一位后加 2变成了 1,得到1-0=1;
0-1,0 在上一步被借一所以就变成了 -1,-1不够减 1,向前借一位后加 2变成了 1,得到1-1=0;
1-0,1在上一步被借一所以就变成了 0,得到 0-0=0;
所以最后 1001001 - 0101101 = 0011100
注意:二进制减法时位数不够向前借一位,然后将该数加 2,所以二进制和十进制减法的区别就是,十进制是向前借 一位,二进制向前借一位后加 2;
(二)二进制加法
二进制加法相对来说就比较简单,二进制相加有四种情况:
0 + 0 = 0;
0 + 1 = 1;
1 + 0 = 1;
1 + 1 = 10;
例如:1001 + 1011 = 10100 (9+11=20)运算过程,从右向左逐位运算:
1+ 1=10,写 0,向前进一;
0+1 = 1,由于后面向前进 1,1+1=10,写 0向前进一;
0+0 = 0,由于后面向前进 1,0+1=1,写1;
1+1 = 10,写 10。
所以最后 1001 + 1011 = 10100
(三)二进制乘法
二进制相乘有四种情况:
0 * 0 = 0;
1 *1 = 0;
0 * 1 = 0;
0 * 1 = 0;
例如:110010 * 1011 = 1000100110 (11*5=55)运算过程,从右向左逐位运算:
二进制的乘法也和十进制的算法相似。
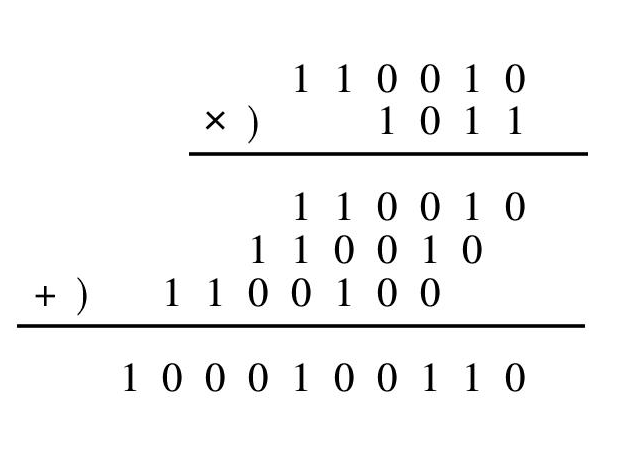
(四)、二进制除法
二进制除法有两种情况(除数只能为1):
0÷1=0;
1÷1=1;
例如:1100 / 100 = 11(12/4 =3)
二、十六进制运算
十六进制:十六进制(英文名称:Hexadecimal),是计算机中数据的一种表示方法。十六进制由0-9,A-F组成,字母不区分大小写。十六进制中的 0-9对应着十进制中的0-9,十六进制中的A-F 对应着十进制中的 10-15。
用 H 表示十六进制
(一)十六进制减法
例如,3D25 - 05C3 = 3762(H) (15653 - 1475 = 3762)
5-3 ,结果为 2;
2-C,即为2-12,2-12不够向前借一位加 16,18-12=6;
D-5,即为13-5,因为被借了一位所以要减1,12-5=7;
3-0,结果为 3;
所以 3D25 - 05C3 = 3762;
注意:用十进制时向前借1位就是借10,而在16进制里向前借1就是借16
(二)十六进制加法
例如,3762(H) + 05C3 = 3D25 (3762 + 1475 = 15653)
2+3,结果为 5;
6+C,即为 6+12,18大于16,取 2 满 16向前进1;
7+5,因为后面向前进了一位,所以结果为 12+1=13(D);
3+0,结果为 0;
所以结果:3762(H) + 05C3 = 3D25
注意:十六进制加法中 满16进 1
三、八进制运算
八进制:Octal,缩写OCT或O,一种以8为基数的计数法,采用0,1,2,3,4,5,6,7八个数,逢八进1。一些编程语言中常常以数字0开始表明该数字是八进制。
用 O表示八进制
(一)八进制减法
例如:534 - 157 = 355 (348 - 111= 237 )
4-7,不够向前借一位加8,即为(4+8)-7,结果为 5;
3-5,因为3已经被借了一变为2,2-5不够再向前借一位加 8,即为 (2+8)-5,结果为 5;
5-1,5被借了一,即为4-1,结果为 3;
所以结果:534 - 157 = 355 ;
注意:用十进制时向前借1位就是借10,而在8 进制里向前借1就是借 8;
(二)八进制加法
例如:355(O) + 157(O) = 534 (237+111 = 348)
5+7,为12大于8,所以结果为 4并且向前进一;
5+5,为10,再加上上一位进的一,11大于8,结果为 3并向前进 1;
3+1,再加上上一位进的一,结果为 4+1=5;
所以结果:355(O) + 157(O) = 534
注意:八进制加法中满 8进 1