魔幻的 2020 让我们怀疑人生是否存在最优解?我们某个时间的决策究竟是否正确?历史不能改变,但却会重演,我们究竟要从过去中学到什么呢?
让我们一起从动态规划中,来找寻这些问题的答案吧~
(咳咳,今天开始回归算法系列,来聊一聊之前的算法文章中没有讲到的内容。
什么是动态规划
动态规划(Dynamic Programic,简称 DP)是一种求解最优解的方法,它是一种特殊的分治思想,利用它可以实现时间复杂度的优化,有时也可以进行空间复杂度的优化,有时是需要更多的空间的(相比其他方法)。
dynamic 是动态的意思,也就是变化的,programing 可以理解为方程(我瞎说的),结合起来就是动态规划是用状态转移方程来求得最优解的算法。
在解释动态规划的时候,我们顺便理一理和它相关的两种思想——分治和贪心算法。
分治
分治是把大问题分解成若干个子问题,这样的能分解性质就是最优子结构的。
最简单的例子就是小明在解决问题 A 的时候,发现问题 A 是由问题 B 和 C 一起组成的,所以他想要解决问题 A,就需要把 B、C 一起去解决。
动态规划
动态规划是分治法的特例。
动态规划比分治法多了一种,就是重叠的子问题。
什么是重叠的子问题呢?举个例子来讲,可爱的小明遇到了一个可爱的问题,那就是问题 A,但是在前面需要解决一连串的问题,我们用A1,A2,A3,A4 ... A来表示,在解决A1之后会用它的解去解决类似的问题A2,
然后再去解决A3,最终再去解决 A,这就是重叠的子问题的典型代表。(下面的例题还会解释这个概念)
贪心
贪心比动态规划更加的特殊,它还需要问题满足另外一个性质——贪心选择性质,每次都可以把原问题分解成为一个子问题。
实际上再用动规的例子来说明贪心,在解决A1,A2,A3,A4 ... A的时候,他发现解决不光有一种重叠子问题的性质在里面,更有趣的是,解决A1需要一种特殊的规则。
例如小明现在在玩电脑游戏,而电脑游戏的最终目的是到达A,而他又发现,只要一直往右边走就能到达最终的目的地了。这就是一种贪心的算法,在每次往右边走,就是一种特殊的规则,而走到目的地A需要很多重复的子问题,也即每次活动一个单位。
入门
其实在很久之前我写的一篇文章中,以斐波那契数列这道基本题为例,详细阐述了从递归到 DP 的优化方法和思路,以及简单题的不简单的答法,大家不妨先去复习一下:
然后我们再来看看一般的动态规划解题思路。
解题思路
回到动态规划,这里有四个基本的概念:
- state(状态表示)
- function(转移方程)
- initial(初始化)
- final state(最终的状态)
在刚开始的时候,我们首先需要构建一个存储数据的表格,一般是数组或者矩阵,然后设定好每一个格子到下一个格子需要的转移方程。
然后去执行重复的步骤,从初始化的状态一直计算到最终需要的状态。
回到小明的例子,刚开始的时候小明需要确定一个 state(A0代表的是什么),然后找到A0与A1之间的关系,从初始化开始一直计算到最终的状态。
接下来,我们以 Leetcode 120 来详细的讲解这个算法。
题目描述

现在我们来分析一下这个题目,首先我们分析一下为什么它是一个动态规划的问题。
题目是要找到一种路径的和,这种路径和是要最小的,也就是求一个最优解。
因为这是路径,我们就是在每一层里面选择一个合适的数字,然后连成一个路径,在这道题目里面,最小的路径是2-3-5-1,在第一层挑了2,在第二层挑了3。也就是说总的问题拆分成了每一层的问题,而每一层之间都有一种依赖性在里面,例如第二层选择了3之后只能在6,5之中选择一个,不能跳到7,这就是重叠子问题。
我们用f[i][j]表示从三角形顶部走到位置 [i][j] 的最小路径和。这里的位置 i, j 指的是三角形中第 i 行第 j 列的位置。
由于只能是从一个节点到相邻的两个节点(树),因此要想走到位置 [i][j],上一步就只能在位置 [i-1][j-1] 或者位置 [i-1][j]。
我们在这两个位置中选择一个路径和较小的来进行转移,状态转移方程为:
f[i][j]=min(f[i−1][j−1],f[i−1][j])+c[i][j],
其中 c[i][j] 指的是triangle[i][j]的数值。
方法一
当设定完通项方程之后,我们还需要设定一些特殊的转化方程:
- 当靠近左边界时,也就是
j = 0时,于是没有f[i-1][j−1]这一项 ,状态转移方程变为:
f[i][0]=f[i−1][0]+c[i][0]
- 当靠近右边界时,我们直接用上一层斜上角位置的数值进行计算:
f[i][i]=f[i−1][i−1]+c[i][i]
最终,我们只需要在 dp 三角形的最后一行找到最小值就可以了。
那么初始的状态是什么呢?
实际上就是刚开始的时候设定 dp 的第一个单位的数值为cp[0][0],也即是dp[0][0] = c[0][0]。
状态转换图如下所示:
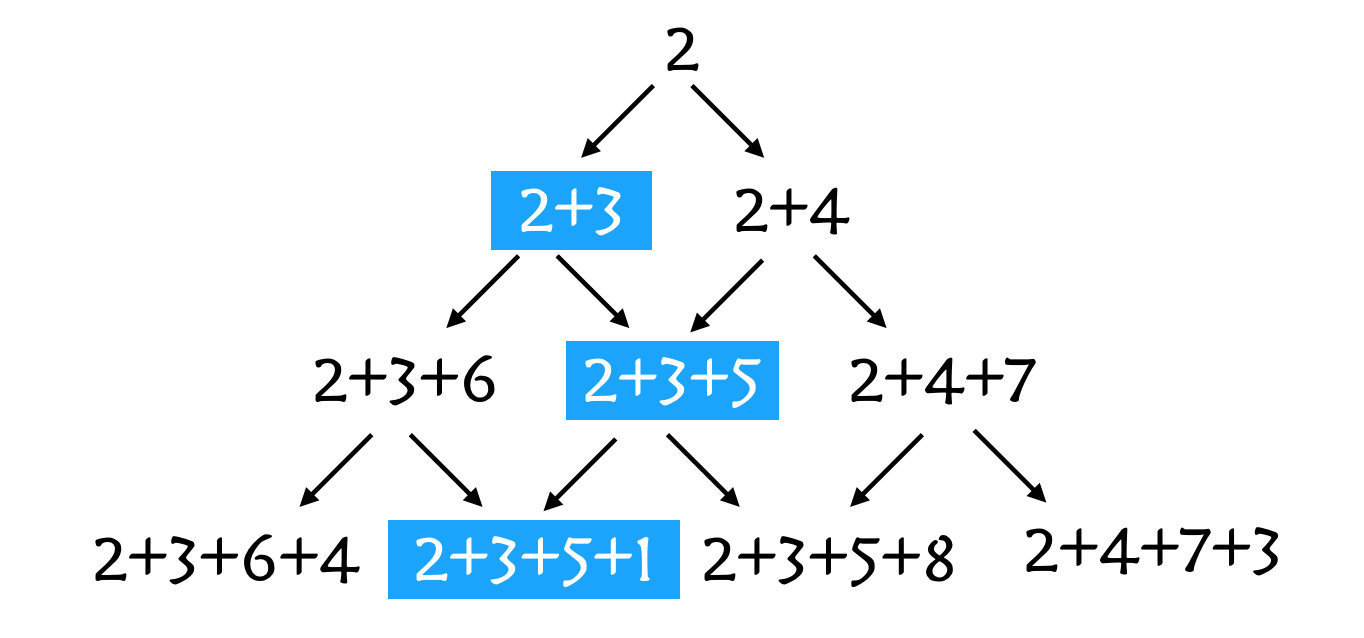
代码如下:
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
// 创建表格
int[][] dp = new int[triangle.size()][triangle.size()];
dp[0][0] = triangle.get(0).get(0);
// 动态规划的方程式
for (int i = 1; i < dp.length; i++) {
for (int j = 0; j <= i; j++) {
int curr = triangle.get(i).get(j);
if (j == 0) {
dp[i][j] = dp[i-1][j] + curr;
} else if (j == i) {
dp[i][j] = dp[i-1][j-1] + curr;
} else {
dp[i][j] = Math.min(dp[i-1][j-1], dp[i-1][j]) + curr;
}
}
}
int res = dp[triangle.size()-1][0];
for (int j = 1; j < triangle.size(); j++) {
res = Math.min(res, dp[triangle.size()-1][j]);
}
return res;
}
}
下面来分析这个问题的时间复杂度以及空间复杂度,一般来说空间复杂度是就是 DP 表格的大小。
在这道问题中是 O(n^2),而对于时间复杂度来说,就是整个 dp 的遍历次数,而在这个问题中我们只进行了一次遍历,也即一个矩阵的遍历,所以是O(n^2)。
而如果想要优化到 O(n),我们需要怎么做呢?
实际上这个就涉及到了一种状态压缩的方法,也即压缩这个状态表。
那么怎么去压缩呢?
这个问题比较简单,因为dp[i][j]仅仅与上一层的状态有关,所以说与前两层的是没有任何关系的,因此我们不必存储这些无关的状态。
实际上最简单的状态压缩就是保留好前两个状态即可,例如在计算第四行的时候,保留第三行以及第二行的状态表,然后交替的进行更新就可以啦。
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
// 只保留最近 2 行
int[][] dp = new int[2][triangle.size()];
dp[0][0] = triangle.get(0).get(0);
for (int i = 1; i < triangle.size(); i++) {
int row = i % 2;
int prevRow = (i-1) % 2;
for (int j = 0; j <= i; j++) {
if (j == 0) {
dp[row][j] = dp[prevRow][j] + triangle.get(i).get(j);
} else if (j == i) {
dp[row][j] = dp[prevRow][j-1] + triangle.get(i).get(j);
} else {
dp[row][j] = Math.min(dp[prevRow][j-1], dp[prevRow][j]) + triangle.get(i).get(j);
}
}
}
int res = dp[(triangle.size() - 1) % 2][0];
for (int j = 1; j < triangle.size(); j++) {
res = Math.min(res, dp[(triangle.size() - 1) % 2][j]);
}
return res;
}
}
这个的空间复杂度是 O(2n),能不能压缩成严格意义上的O(n)呢?
那么再往后是否还能够进行状态的压缩呢?
答案是可以的,我们可以再想一种方程然后达到最优的空间复杂度的目标。
当我们在计算位置 [i][j] 时,f[j+1] 到 f[i] 已经是第 i 行的值,而 f[0] 到 f[j] 仍然是第 i-1 行的值。
此时我们直接通过 f[j] = min(f[j−1], f[j]) + c[i][j]来计算,但是这个时候我们需要j 是倒着遍历的,因为这样才不会影响之前记录下的状态。
如果从 1 开始,那么计算 2 的时候就会用到新的 1 的数值而不是上一层 1 的数值。
代码如下:
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int[] dp = new int[triangle.size()];
dp[0] = triangle.get(0).get(0);
for (int i = 1; i < triangle.size(); i++) {
dp[i] = dp[i-1] + triangle.get(i).get(i);
for (int j = i-1; j > 0; j--) {
dp[j] = Math.min(dp[j-1], dp[j]) + triangle.get(i).get(j);
}
dp[0] += triangle.get(i).get(0);
}
int res = dp[0];
for (int j = 1; j < triangle.size(); j++) {
res = Math.min(res, dp[j]);
}
return res;
}
}
方法 2
方法 1 有点绕,但如果自下向上来理解,就会变得很简单,这个方法也叫 bottom-up,方法 1 则是 top-down。
从结果出发,这个问题是一个发散三角树的问题,从最后一行出发,然后每一行每一行的进行递推,那么第一行就是最终的结果了。
举个最简单的例子:
1
1 2
如果从最底下往上出发,实际上找最小值方法的规律很容易找到,那就是在第二行[1, 2]里面选择一个就可以了,因为他们两个都要走到根节点。
也就是在下一行的两个数里面取个小的就行了,那么结果就是第一行的数值。
我们先用二维的转移矩阵来解释这个问题,用这种方法也不需要考虑方法 1 里面的边界条件了:
dp[i][j] = min(dp[i+1][j], dp[i+1][j+1]) + c[i][j]
状态转换图如下所示:

class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int[][] dp = new int[triangle.size()][triangle.size()];
// 创建 DP 空间
for (int i = 0; i < triangle.size(); i++) {
dp[triangle.size() - 1][i] = triangle.get(triangle.size() - 1).get(i);
}
for (int i = triangle.size() - 2; i >= 0; i--) {
for (int j = 0; j < triangle.get(i).size(); j++) {
dp[i][j] = Math.min(dp[i+1][j], dp[i+1][j+1]) + triangle.get(i).get(j);
}
}
return dp[0][0];
}
}
那么在进行状态压缩的时候,我们该怎么去做呢?
实际上就是只用一个状态表来表示所有的。
因为只是和上一个状态相关,所以说可以表示成如下的形式:
dp[j] = min(dp[j], dp[j + 1]) + triangle[i][j],
我们只用 j 来代表当前的状态,然后最终输出dp[0]即可。
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int[] dp = new int[triangle.size()];
// 创建 DP 空间
for (int i = 0; i < triangle.size(); i++) {
dp[i] = triangle.get(triangle.size() - 1).get(i);
}
for (int i = triangle.size() - 2; i >= 0; i--) {
for (int j = 0; j <= i; j++) {
dp[j] = Math.min(dp[j], dp[j+1]) + triangle.get(i).get(j);
}
}
return dp[0];
}
}
总结
以上就是动态规划解题方法的粗浅介绍,总的来说,我们需要注意动态规划的这么几件事情。
- 确定是否需要用动态规划;
- 确定动态规划的四个部分;
- 写代码。
实际上难点就是转移方程,这个确实需要大量的积累才能够在面试的时候看穿,甚至有些题没见过的话就是想不出来的。
但是没见过就做不出来的题面试一般也不会考,所以大家也不用太担心,重点还是掌握方法,举一反三。
接下来我也会归纳总结一些动态规划的常见题型,和大家一起探索最优解。
更多算法文章,建议收藏这个链接:
我是小齐,后端开发工程师,坐标纽约,曾在投行做 Quant,后加入科技公司 FLAG 中的一家。
业余时间打理公粽号【NYCSDE】,更新略少,干货很多,建议加个星标防止错过。