问题:
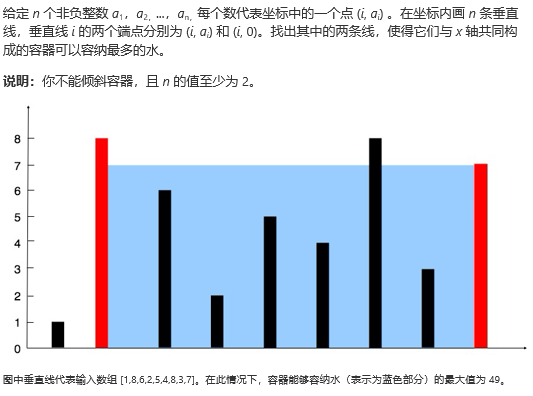

一、暴力解法:
package com.example.demo; public class Test11 { /** * 给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。 * 在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线, * 使得它们与 x 轴共同构成的容器可以容纳最多的水。 * * @param height * @return */ public int maxArea(int[] height) { //暴力解法,双层for int maxArea = 0; for (int i = 0; i < height.length; i++) { for (int j = i + 1; j < height.length; j++) { maxArea = Math.max(maxArea, (j - i) * Math.min(height[i], height[j])); } } return maxArea; } public static void main(String[] args) { Test11 t = new Test11(); int[] arr = {1, 8, 6, 2, 5, 4, 8, 3, 7}; int i = t.maxArea(arr); System.out.println(i); } }
二、双支针
package com.example.demo; public class Test11 { /** * 给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。 * 在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线, * 使得它们与 x 轴共同构成的容器可以容纳最多的水。 * * @param height * @return */ public int maxArea(int[] height) { //双指针 int maxArea = 0; int left = 0, right = height.length - 1; while (left < right) { maxArea = Math.max(maxArea, (right - left) * Math.min(height[right], height[left])); if (height[right] < height[left]) { right--; } else { left++; } } return maxArea; } public static void main(String[] args) { Test11 t = new Test11(); int[] arr = {1, 8, 6, 2, 5, 4, 8, 3, 7}; int i = t.maxArea(arr); System.out.println(i); } }