构造一棵二叉排序树的目的,其实并不是为了排序,而是为了提高查找和插入删除的效率。
那么什么是二叉排序树呢?二叉排序树具有以下几个特点。
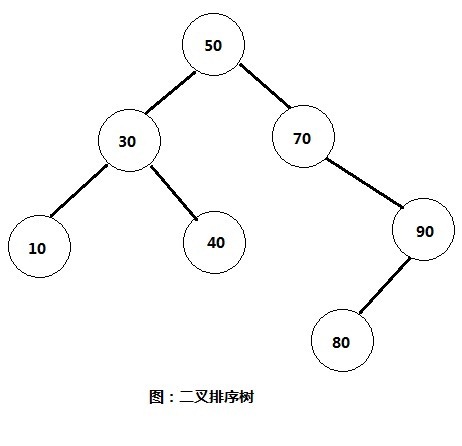
1,若根节点有左子树,则左子树的所有节点都比根节点小。
2,若根节点有右子树,则右子树的所有节点都比根节点大。
3,根节点的左,右子树也分别为二叉排序树。
下面是二叉排序树的图示,通过图可以加深对二叉排序树的理解。
下面是二叉排序树常见的操作及思路。
1,插入节点
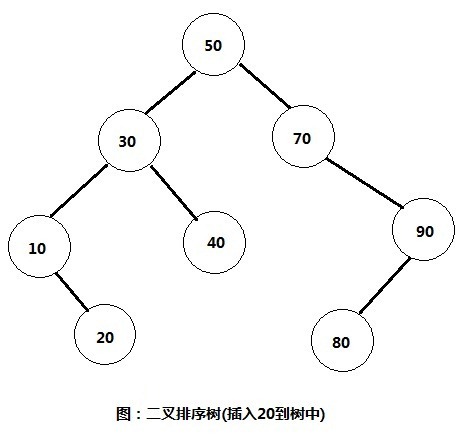
思路:比如我们要插入数字20到这棵二叉排序树中。那么步骤如下:
1) 首先将20与根节点进行比较,发现比根节点小,所以继续与根节点的左子树30比较。
2) 发现20比30也要小,所以继续与30的左子树10进行比较。
3) 发现20比10要大,所以就将20插入到10的右子树中。
此时二叉排序树效果如图:
2,查找节点
比如我们要查找节点10,那么思路如下:
1) 还是一样,首先将10与根节点50进行比较大小,发现比根节点要小,所以继续与根节点的左子树30进行比较。
2) 发现10比左子树30要小,所以继续与30的左子树10进行比较。
3) 发现两值相等,即查找成功,返回10的位置。
过程与插入相同,这里就不贴图了。
3,删除节点
删除节点的情况相对复杂,主要分以下三种情形:
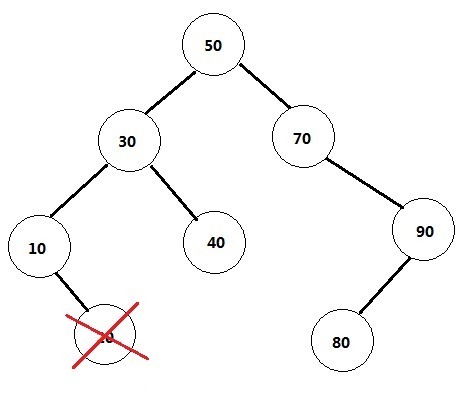
1) 删除的是叶节点(即没有孩子节点的)。比如20,删除它不会破坏原来树的结构,最简单。如图所示。
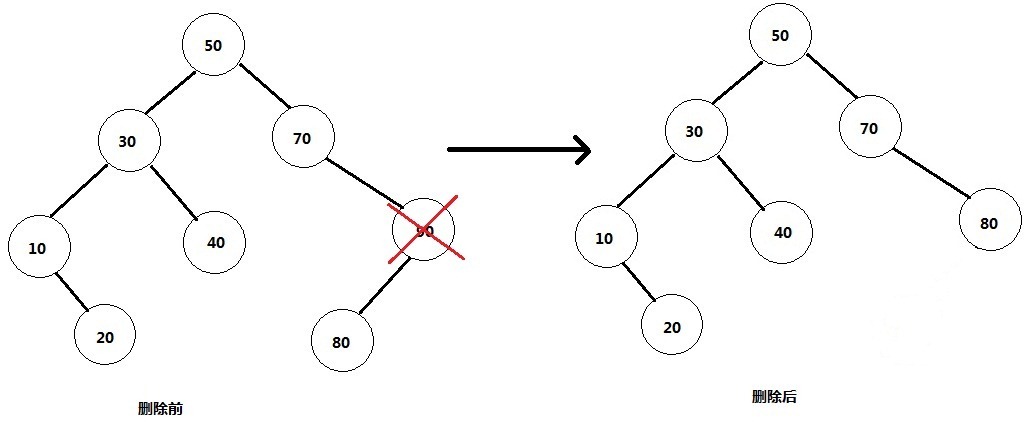
2) 删除的是单孩子节点。比如90,删除它后需要将它的孩子节点与自己的父节点相连。情形比第一种复杂一些。
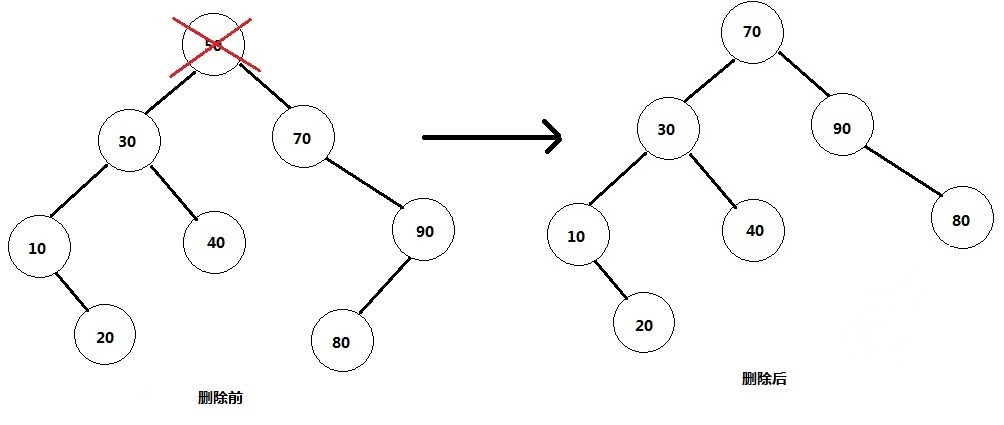
3) 删除的是有左右孩子的节点。比如根节点50,这里有一个问题就是删除它后将谁做为根节点的问题?利用二叉树的中序遍历,就是右节点的左子树的最左孩子。
分析完了,有了思路之后,下面就开始写代码来实现这些功能了。
C#版:
namespace DS.BLL
{
/// <summary>
/// Description:二叉排序树的常见操作
/// Author:McgradyLu
/// Time:8/24/2013 4:12:18 PM
/// </summary>
public class BSTreeBLL
{
/// <summary>
/// 创建二叉排序树
/// </summary>
/// <param name="list"></param>
/// <returns></returns>
public static BSTree Create(List<int> list)
{
//创建根节点
BSTree bsTree = new BSTree()
{
Data=list[0],
Left=null,
Right=null
};
//将list中的节点一个一个地插入到二叉排序树中
for (int i = 1; i < list.Count; i++) //注意这里从1开始,因为0位置上元素已经给了根节点
{
bool isExcute = false;
Insert(bsTree, list[i], ref isExcute);
}
return bsTree;
}
/// <summary>
/// 插入节点
/// </summary>
/// <param name="bsTree">二叉排序树</param>
/// <param name="key">待插入值</param>
/// <param name="isExcute">是否执行了if语句(节点是否插入)</param>
public static void Insert(BSTree bsTree, int key, ref bool isExcute)
{
if (bsTree == null) return;
//如果小于根节点,遍历左子树,否则遍历右子树(找到当前要插入节点的父节点)
if (key < bsTree.Data) Insert(bsTree.Left, key, ref isExcute);
else Insert(bsTree.Right, key, ref isExcute);
if (!isExcute)
{
//创建当前节点
BSTree current = new BSTree() {
Data=key,
Left=null,
Right=null
};
//插入到父节点中
if (key < bsTree.Data) bsTree.Left = current;
else bsTree.Right = current;
isExcute = true;
}
}
/// <summary>
/// 中序遍历
/// </summary>
/// <param name="bsTree"></param>
public static void LDR(BSTree bsTree)
{
if (bsTree != null)
{
//遍历左子树
LDR(bsTree.Left);
//输出节点数据
Console.Write(bsTree.Data+" ");
//遍历右子树
LDR(bsTree.Right);
}
}
/// <summary>
/// 查找节点
/// </summary>
/// <param name="bsTree">待查找的二叉排序树</param>
/// <param name="key"></param>
/// <returns>true表示查找成功,false表示查找失败</returns>
public static bool Search(BSTree bsTree, int key)
{
//遍历完没有找到,查找失败
if (bsTree == null) return false;
//要查找的元素为当前节点,查找成功
if (key == bsTree.Data) return true;
//继续去当前节点的左子树中查找,否则去当前节点的右子树中查找
if (key < bsTree.Data) return Search(bsTree.Left, key);
else return Search(bsTree.Right,key);
}
/// <summary>
/// 删除节点
/// </summary>
/// <param name="bsTree"></param>
/// <param name="key"></param>
public static void Delete(ref BSTree bsTree, int key)
{
//空树
if (bsTree == null) return;
//判断是否是要删除的节点
if (key == bsTree.Data)
{
//第一种情况:叶子节点(没有孩子节点)
if (bsTree.Left == null && bsTree.Right == null)
{
bsTree = null;
return;
}
//第二种情况:仅有左子树
if (bsTree.Left != null && bsTree.Right == null)
{
bsTree = bsTree.Left;
return;
}
//第三种情况:仅有右子树
if (bsTree.Left == null && bsTree.Right != null)
{
bsTree = bsTree.Right;
return;
}
//第四种情况:有左,右子树
if (bsTree.Left != null && bsTree.Right != null)
{
//利用中序遍历找到右节点的左子树的最左孩子
var node = bsTree.Right;
while (node.Left != null)
{
node = node.Left;
}
node.Left = bsTree.Left;
if (node.Right == null)
{
Delete(ref bsTree,node.Data);
node.Right = bsTree.Right;
}
bsTree = node;
}
}
//遍历找到要删除的节点
if (key < bsTree.Data)
{
Delete(ref bsTree.Left, key);
}
else
{
Delete(ref bsTree.Right, key);
}
}
}
/// <summary>
/// 封装二叉排序树结构
/// </summary>
public class BSTree
{
public int Data;
public BSTree Left;
public BSTree Right;
}
}
namespace BSTSearch.CSharp
{
class Program
{
static void Main(string[] args)
{
List<int> list = new List<int> { 50,30,70,10,40,90,80};
Console.WriteLine("***************创建二叉排序树***************");
BSTree bsTree = BSTreeBLL.Create(list);
Console.Write("中序遍历的原始数据:
");
BSTreeBLL.LDR(bsTree);
Console.WriteLine("
********************查找节点********************");
Console.WriteLine("元素40是否在树中:{0}",BSTreeBLL.Search(bsTree,40));
Console.WriteLine("
********************插入节点********************");
Console.WriteLine("将元素20插入到树中");
bool isExcute=false;
BSTreeBLL.Insert(bsTree,20,ref isExcute);
Console.Write("中序遍历后:
");
BSTreeBLL.LDR(bsTree);
Console.WriteLine("
********************删除节点1********************");
Console.WriteLine("删除叶子节点20,
中序遍历后:
");
BSTreeBLL.Delete(ref bsTree,20);
BSTreeBLL.LDR(bsTree);
Console.WriteLine("
********************删除节点2********************");
Console.WriteLine("删除单孩子节点90,
中序遍历后:
");
BSTreeBLL.Delete(ref bsTree, 90);
BSTreeBLL.LDR(bsTree);
Console.WriteLine("
********************删除节点2********************");
Console.WriteLine("删除根节点50,
中序遍历后:
");
BSTreeBLL.Delete(ref bsTree, 50);
BSTreeBLL.LDR(bsTree);
Console.ReadKey();
}
}
}
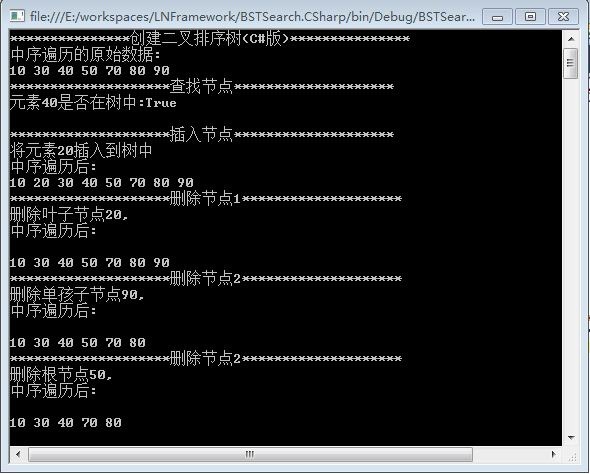
程序输出结果如图: