




建立神经网络的主要步骤是:
1. 定义模型结构(例如输入特征的数量)
2. 初始化模型的参数
3. 循环:
# 3.1 计算当前损失(正向传播)
# 3.2 计算当前梯度(反向传播)
# 3.3 更新参数(梯度下降)
实现代码
#单层神经网络,不含隐含层
import numpy as np
import matplotlib.pyplot as plt
import h5py #是与H5文件中存储的数据集进行交互的常用软件包。
from lr_utils import load_dataset #在本文的资料包里,一个加载资料包里面的数据的简单功能的库
def load_dataset():
train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
classes = np.array(test_dataset["list_classes"][:]) # the list of classes
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes
# train_set_x_orig :保存的是训练集里面的图像数据(本训练集有209张64x64的图像)。
# train_set_y_orig :保存的是训练集的图像对应的分类值(【0 | 1】,0表示不是猫,1表示是猫)。
# test_set_x_orig :保存的是测试集里面的图像数据(本训练集有50张64x64的图像)。
# test_set_y_orig : 保存的是测试集的图像对应的分类值(【0 | 1】,0表示不是猫,1表示是猫)。
# classes : 保存的是以bytes类型保存的两个字符串数据,数据为:[b’non-cat’ b’cat’]。
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = load_dataset()
#查看第26张图片
index = 25
plt.imshow(train_set_x_orig[index])
plt.show()
print(str(train_set_y))#查看训练集里面的标签
#打印出当前的训练标签值
#使用np.squeeze的目的是压缩维度,【未压缩】train_set_y[:,index]的值为[1] , 【压缩后】np.squeeze(train_set_y[:,index])的值为1
#print("【使用np.squeeze:" + str(np.squeeze(train_set_y[:,index])) + ",不使用np.squeeze: " + str(train_set_y[:,index]) + "】")
#只有压缩后的值才能进行解码操作
# print(train_set_y)
# print(train_set_y[:,index]) #[1]
# print(np.squeeze(train_set_y[:,index]))#1
# print("y=" + str(train_set_y[:,index]) + ", it's a " + classes[np.squeeze(train_set_y[:,index])].decode("utf-8") + "' picture")
# 结果:y=[1], it's a cat' picture
m_train = train_set_y.shape[1] #训练集里图片的数量。
m_test = test_set_y.shape[1] #测试集里图片的数量。
num_px = train_set_x_orig.shape[1] #训练、测试集里面的图片的宽度和高度(均为64x64)。
#现在看一看我们加载的东西的具体情况
# print ("训练集的数量: m_train = " + str(m_train)) #m_train = 209
# print ("测试集的数量 : m_test = " + str(m_test)) #m_test = 50
# print ("每张图片的宽/高 : num_px = " + str(num_px)) #num_px = 64 均为64
# print ("每张图片的大小 : (" + str(num_px) + ", " + str(num_px) + ", 3)") #(64, 64, 3)
# print ("训练集_图片的维数 : " + str(train_set_x_orig.shape)) #(209, 64, 64, 3) [batch, height, width, channels]
# print ("训练集_标签的维数 : " + str(train_set_y.shape)) #(1, 209)
# print ("测试集_图片的维数: " + str(test_set_x_orig.shape)) #(50, 64, 64, 3)
# print ("测试集_标签的维数: " + str(test_set_y.shape))#(1, 50)
# 把维度为(64,64,3)的numpy数组构造为(64*64*3,1)的数组
# X_flatten = X.reshape(X.shape[0],-1).T # X.T是X的转置
# 当你想将形状(a,b,c,d)的矩阵X平铺成形状(b * c * d,a)的矩阵X_flatten时,可以使用以下代码:
# 这一段意思是指把数组变为209行的矩阵(因为训练集里有209张图片),但是我懒得算列有多少,
# 于是我就用-1告诉程序你帮我算,最后程序算出来时12288列,我再最后用一个T表示转置,这就变成了12288行,209列。测试集亦如此。
train_set_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0],-1).T
test_set_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0],-1).T
# print ("训练集降维最后的维度: " + str(train_set_x_flatten.shape)) #(12288, 209)
# print ("训练集_标签的维数 : " + str(train_set_y.shape)) #(1, 209)
# print ("测试集降维之后的维度: " + str(test_set_x_flatten.shape)) #(12288, 50)
# print ("测试集_标签的维数 : " + str(test_set_y.shape)) #(1, 50)
# 为了表示彩色图像,必须为每个像素指定红色,绿色和蓝色通道(RGB),因此像素值实际上是从0到255范围内的三个数字的向量。
# 机器学习中一个常见的预处理步骤是对数据集进行居中和标准化,这意味着可以减去每个示例中整个numpy数组的平均值,
# 然后将每个示例除以整个numpy数组的标准偏差。但对于图片数据集,它更简单,更方便,几乎可以将数据集的每一行除以255(像素通道的最大值),
# 因为在RGB中不存在比255大的数据,所以我们可以放心的除以255,让标准化的数据位于[0,1]之间,现在标准化我们的数据集:
train_set_x = train_set_x_flatten / 255
test_set_x = test_set_x_flatten / 255
def sigmoid(z):
"""参数:
z - 任何大小的标量或numpy数组。
返回:
s - sigmoid(z)"""
s = 1 / (1 + np.exp(-z))
return s
#测试sigmod
# print(sigmoid(0)) #0.5
# print(sigmoid(9.2))# 0.9998...
#初始化参数w和b
def initialize_with_zeros(dim):
"""此函数为w创建一个维度为(dim,1)的0向量,并将b初始化为0。
参数:
dim - 我们想要的w矢量的大小(或者这种情况下的参数数量)
返回:
w - 维度为(dim,1)的初始化向量。
b - 初始化的标量(对应于偏差)"""
w = np.zeros(shape=(dim,1))
b = 0
# 使用断言来确保我要的数据是正确的
assert(w.shape == (dim,1))#w的维度是(dim,1)
assert(isinstance(b,float) or isinstance(b,int)) #b的类型是float或者是int
return (w,b)
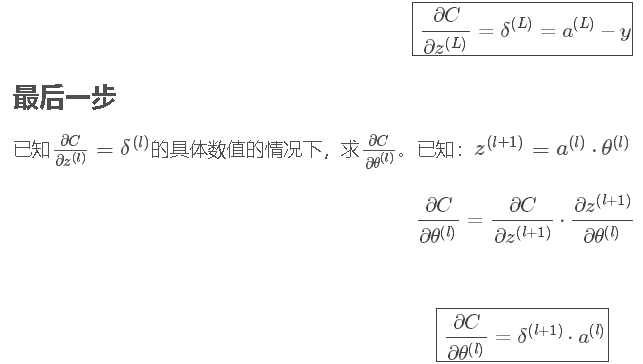
# 我们现在要实现一个计算成本函数及其渐变的函数propagate()。
def propagate(w,b,X,Y):
"""实现前向和后向传播的成本函数及其梯度。
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 矩阵类型为(num_px * num_px * 3,训练数量)
Y - 真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据数量)
返回:
cost- 逻辑回归的负对数似然成本
dw - 相对于w的损失梯度,因此与w相同的形状
db - 相对于b的损失梯度,因此与b的形状相同"""
m = X.shape[1]
#正向传播
A = sigmoid(np.dot(w.T,X) + b) #计算激活值
cost = (-1/m) * np.sum(Y * np.log(A) + (1-Y) * (np.log(1-A)))#计算成本
#反向传播
dw = (1/m) * np.dot(X,(A-Y).T)
db = (1/m) * np.sum(A-Y)
assert (dw.shape == w.shape)
assert (db.dtype == float)
cost = np.squeeze(cost)
assert (cost.shape == ())
#创建一个字典,把dw和db保存起来
grads = {
"dw":dw,
"db":db
}
return (grads,cost)
w,b,X,Y = np.array([[1],[2]]),2,np.array([[1,2],[3,4]]),np.array([[1,0]])
grads,cost = propagate(w,b,X,Y)
# print(grads['dw'])
#[[0.99993216]
# [1.99980262]]
# print(grads['db'])#0.49993523062470574
# print(cost)#6.000064773192205
# 现在,我要使用渐变下降更新参数。
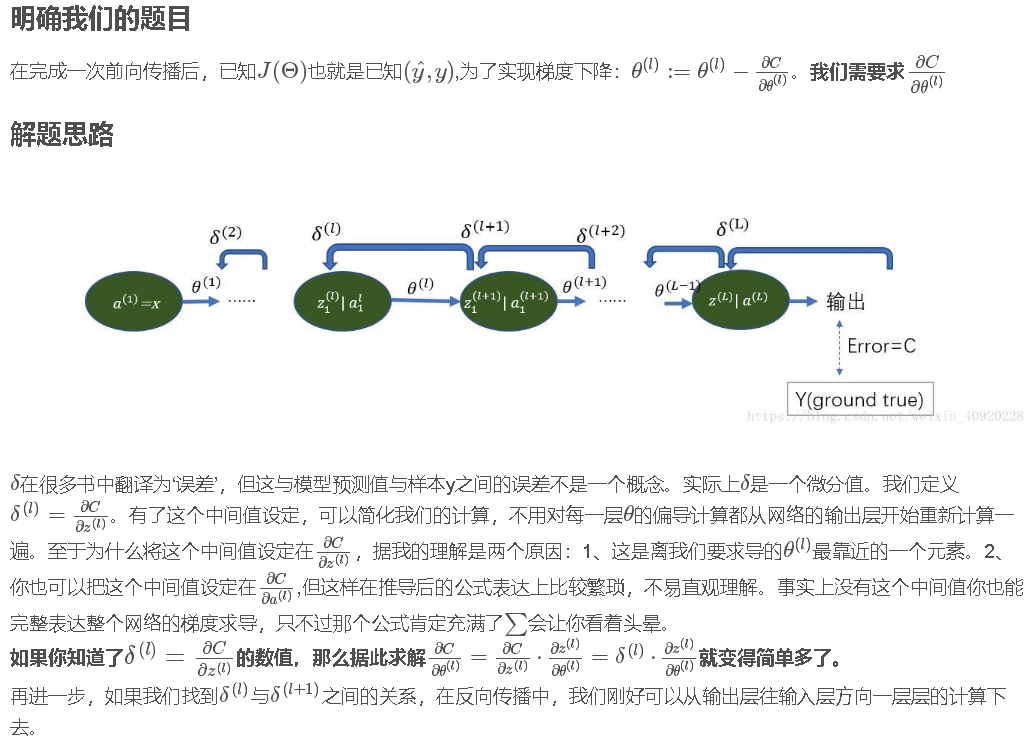
# 目标是通过最小化成本函数 JJ 来学习 ww和bb 。对于参数 θθ ,更新规则是 θ=θ−α dθθ=θ−α dθ,其中 αα 是学习率。
def optimize(w,b,X,Y,num_iterations,learning_rate,print_cost=False):
"""此函数通过运行梯度下降算法来优化w和b
参数:
:param w:权重,大小不等的数组(num_px * num_px * 3,1)
:param b:偏差,一个标量
:param X:维度为(num_px * num_px * 3,训练数据的数量)的数组。
:param Y:真正的“标签”矢量(如果非猫则为0,如果是猫则为1),矩阵维度为(1,训练数据的数量)
:param num_iterations:优化循环的迭代次数
:param learning_rate:梯度下降更新规则的学习率
:param print_cost:每100步打印一次损失值
:return:
返回:
params - 包含权重w和偏差b的字典
grads - 包含权重和偏差相对于成本函数的梯度的字典
成本 - 优化期间计算的所有成本列表,将用于绘制学习曲线。
提示:
我们需要写下两个步骤并遍历它们:
1)计算当前参数的成本和梯度,使用propagate()。
2)使用w和b的梯度下降法则更新参数。
"""
costs = []
for i in range(num_iterations):
grads,cost = propagate(w,b,X,Y)
dw = grads['dw']
db = grads['db']
w = w - learning_rate * dw
b = b - learning_rate * db
#记录成本
if i % 100 == 0:
costs.append(cost)
#打印成本数据
if print_cost and (i % 100) == 0:
print("迭代的次数:%i,误差值:%f"%(i,cost))
params = {"w":w,
"b":b}
grads = {"dw":dw,
"db":db}
return (params,grads,costs)
#测试
# w, b, X, Y = np.array([[1], [2]]), 2, np.array([[1,2], [3,4]]), np.array([[1, 0]])
# params,grads,costs = optimize(w,b,X,Y,num_iterations=100,learning_rate=0.009,print_cost=False)
# print("w"+str(params['w']))
# w[[0.1124579 ]
# [0.23106775]]
# print("b"+str(params['b']))#b1.5593049248448891
# print("dw"+str(grads['dw']))
# dw[[0.90158428]
# [1.76250842]]
# print("db"+str(grads['db']))
# db0.4304620716786828
# ptimize函数会输出已学习的w和b的值,我们可以使用w和b来预测数据集X的标签。
# 现在我们要实现预测函数predict()。计算预测有两个步骤:
# 1.计算 Y^=A=σ(wTX+b)
# 2.将a的值变为0(如果激活值<= 0.5)或者为1(如果激活值> 0.5),
# 然后将预测值存储在向量Y_prediction中。
def predict(w,b,X):
"""使用学习逻辑回归参数logistic (w,b)预测标签是0还是1,
参数:
w - 权重,大小不等的数组(num_px * num_px * 3,1)
b - 偏差,一个标量
X - 维度为(num_px * num_px * 3,训练数据的数量)的数据
返回:
Y_prediction - 包含X中所有图片的所有预测【0 | 1】的一个numpy数组(向量)"""
m = X.shape[1] #图片的数量
Y_prediction = np.zeros((1,m))
w = w.reshape(X.shape[0],1)
#预测猫在图片中出现的概率
A = sigmoid(np.dot(w.T,X) + b)
for i in range(A.shape[1]):
Y_prediction[0,i] = 1 if A[0,i] > 0.5 else 0
assert(Y_prediction.shape == (1,m))
return Y_prediction
#测试
w,b,X,Y = np.array([[1],[2]]),2,np.array([[1,2],[3,4]]),np.array([[1,0]])
# print("predict",str(predict(w,b,X)))
#predict [[1. 1.]]
# 就目前而言,我们基本上把所有的东西都做完了,现在我们要把这些函数统统整合到一个model()函数中,
# 届时只需要调用一个model()就基本上完成所有的事了。
def model(X_train , Y_train , X_test , Y_test , num_iterations = 2000 , learning_rate = 0.5 , print_cost = False):
"""通过调用之前实现的函数来构建逻辑回归模型
参数:
X_train - numpy的数组,维度为(num_px * num_px * 3,m_train)的训练集
Y_train - numpy的数组,维度为(1,m_train)(矢量)的训练标签集
X_test - numpy的数组,维度为(num_px * num_px * 3,m_test)的测试集
Y_test - numpy的数组,维度为(1,m_test)的(向量)的测试标签集
num_iterations - 表示用于优化参数的迭代次数的超参数
learning_rate - 表示optimize()更新规则中使用的学习速率的超参数
print_cost - 设置为true以每100次迭代打印成本
返回:
d - 包含有关模型信息的字典。"""
w, b = initialize_with_zeros (X_train.shape[0])
parameters, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate, print_cost)
# 从字典“参数”中检索参数w和b
w, b = parameters["w"], parameters["b"]
# 预测测试/训练集的例子
Y_prediction_test = predict (w, b, X_test)
Y_prediction_train = predict (w, b, X_train)
# 打印训练后的准确性
print ("训练集准确性:", format (100 - np.mean (np.abs(Y_prediction_train - Y_train)) * 100), "%")
print ("测试集准确性:", format (100 - np.mean (np.abs(Y_prediction_test - Y_test)) * 100), "%")
d = {
"costs": costs,
"Y_prediction_test": Y_prediction_test,
"Y_prediciton_train": Y_prediction_train,
"w": w,
"b": b,
"learning_rate": learning_rate,
"num_iterations": num_iterations}
return d
print("====================测试model====================")
#这里加载的是真实的数据,请参见上面的代码部分。
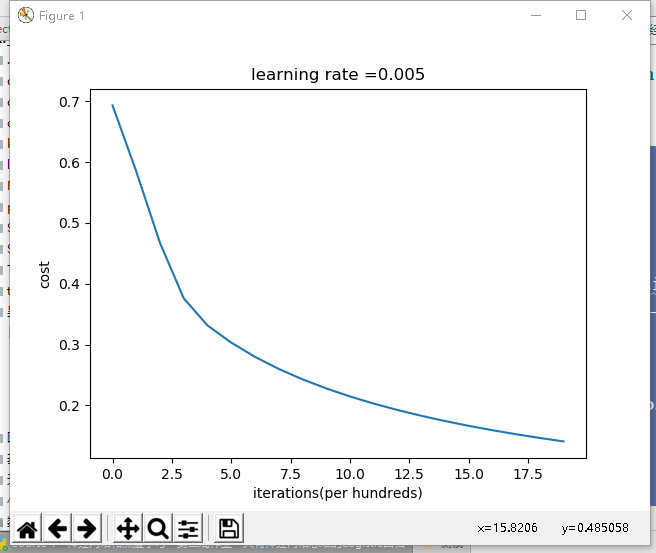
d = model(train_set_x, train_set_y, test_set_x, test_set_y, num_iterations = 2000, learning_rate = 0.005, print_cost = True)
# 画图
print(d['costs'])
costs = np.squeeze(d['costs'])
print(costs)
plt.plot(costs)
plt.xlabel('iterations(per hundreds)')
plt.ylabel('cost')
plt.title('learning rate ='+str(d['learning_rate']))
plt.show()
====================测试model====================
迭代的次数:0,误差值:0.693147
迭代的次数:100,误差值:0.584508
迭代的次数:200,误差值:0.466949
迭代的次数:300,误差值:0.376007
迭代的次数:400,误差值:0.331463
迭代的次数:500,误差值:0.303273
迭代的次数:600,误差值:0.279880
迭代的次数:700,误差值:0.260042
迭代的次数:800,误差值:0.242941
迭代的次数:900,误差值:0.228004
迭代的次数:1000,误差值:0.214820
迭代的次数:1100,误差值:0.203078
迭代的次数:1200,误差值:0.192544
迭代的次数:1300,误差值:0.183033
迭代的次数:1400,误差值:0.174399
迭代的次数:1500,误差值:0.166521
迭代的次数:1600,误差值:0.159305
迭代的次数:1700,误差值:0.152667
迭代的次数:1800,误差值:0.146542
迭代的次数:1900,误差值:0.140872
训练集准确性: 99.04306220095694 %
测试集准确性: 70.0 %
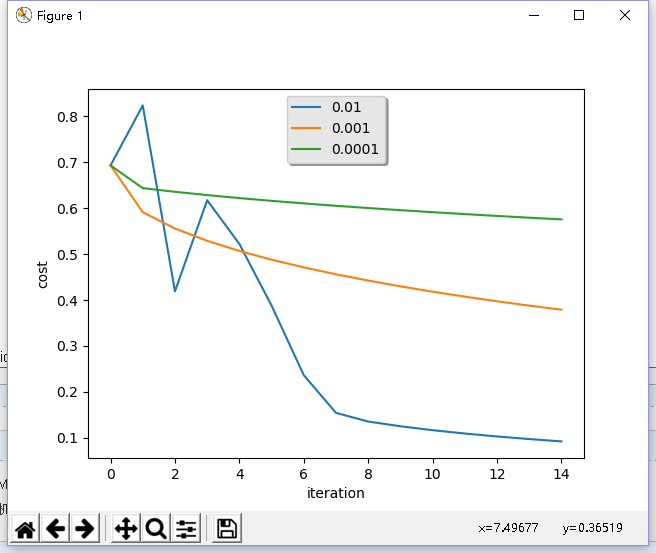
learning_rates = [0.01,0.001,0.0001]
models = {}
for i in learning_rates:
print("learning_rate",i)
models[str(i)] = model(train_set_x,train_set_y,test_set_x,test_set_y,num_iterations=1500,learning_rate=i,print_cost=False)
print('
'+'------------------------------------------------'+'
')
for i in learning_rates:
plt.plot(np.squeeze(models[str(i)]['costs']),label=str(models[str(i)]['learning_rate']))
plt.ylabel('cost')
plt.xlabel('iteration')
legend = plt.legend(loc='upper center',shadow=True)
frame = legend.get_frame()
frame.set_facecolor('0.90')
plt.show()
====================测试model====================
learning_rate 0.01
训练集准确性: 99.52153110047847 %
测试集准确性: 68.0 %
------------------------------------------------
learning_rate 0.001
训练集准确性: 88.99521531100478 %
测试集准确性: 64.0 %
------------------------------------------------
learning_rate 0.0001
训练集准确性: 68.42105263157895 %
测试集准确性: 36.0 %
------------------------------------------------
参考
[1]: https://blog.csdn.net/weixin_40920228/article/details/80709216
神经网络反向传播推导超简单
[2]: https://blog.csdn.net/u013733326/article/details/79639509
Course 1 - 神经网络和深度学习 - 第二周作业