六、移动窗口函数
移动窗口和指数加权函数类别如↓:

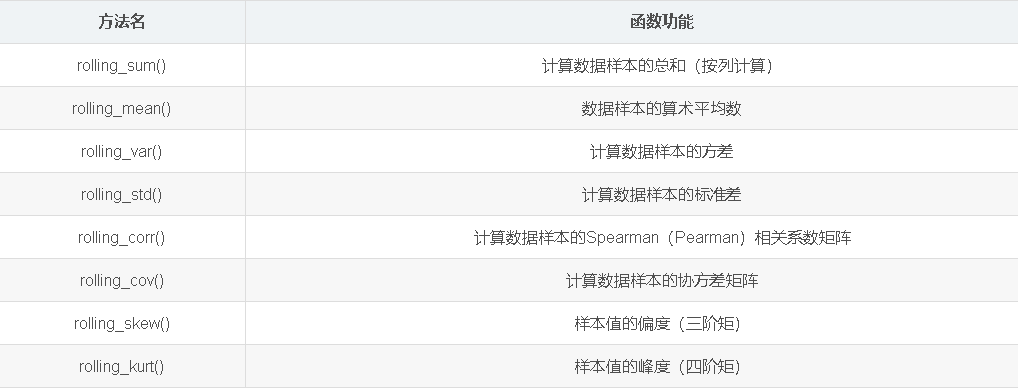
rolling_mean 移动窗口的均值
pandas.rolling_mean(arg, window, min_periods=None, freq=None, center=False, how=None, **kwargs)
rolling_median 移动窗口的中位数
pandas.rolling_median(arg, window, min_periods=None, freq=None, center=False, how='median', **kwargs)
rolling_var 移动窗口的方差
pandas.rolling_var(arg, window, min_periods=None, freq=None, center=False, how=None, **kwargs)
rolling_std 移动窗口的标准差
pandas.rolling_std(arg, window, min_periods=None, freq=None, center=False, how=None, **kwargs)
rolling_min 移动窗口的最小值
pandas.rolling_min(arg, window, min_periods=None, freq=None, center=False, how='min', **kwargs)
rolling_max 移动窗口的最大值
pandas.rolling_min(arg, window, min_periods=None, freq=None, center=False, how='min', **kwargs)
rolling_corr 移动窗口的相关系数
pandas.rolling_corr(arg1, arg2=None, window=None, min_periods=None, freq=None, center=False, pairwise=None, how=None)
rolling_corr_pairwise 配对数据的相关系数
等价于: rolling_corr(…, pairwise=True)
pandas.rolling_corr_pairwise(df1, df2=None, window=None, min_periods=None, freq=None, center=False)
rolling_cov 移动窗口的协方差
pandas.rolling_cov(arg1, arg2=None, window=None, min_periods=None, freq=None, center=False, pairwise=None, how=None, ddof=1)
rolling_skew 移动窗口的偏度(三阶矩)
pandas.rolling_skew(arg, window, min_periods=None, freq=None, center=False, how=None, **kwargs)
rolling_kurt 移动窗口的峰度(四阶矩)
pandas.rolling_kurt(arg, window, min_periods=None, freq=None, center=False, how=None, **kwargs)
rolling_apply 对移动窗口应用普通数组函数
pandas.rolling_apply(arg, window, func, min_periods=None, freq=None, center=False, args=(), kwargs={})
rolling_window 移动窗口
pandas.rolling_window(arg, window=None, win_type=None, min_periods=None, freq=None, center=False, mean=True, axis=0, how=None, **kwargs)
ewma 指数加权移动
ewma(arg[, com, span, halflife, ...])
ewmstd 指数加权移动标准差
ewmstd(arg[, com, span, halflife, ...])
ewmvar 指数加权移动方差
ewmvar(arg[, com, span, halflife, ...])
ewmcorr 指数加权移动相关系数
ewmcorr(arg1[, arg2, com, span, halflife, ...])
ewmcov 指数加权移动协方差
ewmcov(arg1[, arg2, com, span, halflife, ...])
- rolling_系列是pandas的函数,不是DataFrame或Series对象的方法,其格式为pd.rolling_mean(D,k),其中每k列计算一次平均值,滚动计算。
- 新版用DataFrame.rolling(...).mean()取代了pd.rolling_mean(DataFrame,...)
1. 简单移动平均
在移动窗口上计算的各种统计函数也是一类常见于时间序列的数组变换。我们将他们称谓移动窗口函数-moving window function其中还包括那些窗口不定长的函数,跟其他函数一样,移动窗口会自动排除缺失值。
DataFrame.rolling(window, min_periods=None, center=False, win_type=None, on=None, axis=0, closed=None)
- window: 也可以省略不写。表示时间窗的大小,注意有两种形式(int or offset)。如果使用int,则数值表示计算统计量的观测值的数量即向前几个数据。如果是offset类型,表示时间窗的大小。offset详解
- min_periods:每个窗口最少包含的观测值数量,小于这个值的窗口结果为NA。值可以是int,默认None。offset情况下,默认为1。
- center: 把窗口的标签设置为居中。布尔型,默认False,居右
- win_type: 窗口的类型。截取窗的各种函数。字符串类型,默认为None。各种类型
- on: 可选参数。对于dataframe而言,指定要计算滚动窗口的列。值为列名。
- axis: int、字符串,默认为0,即对列进行计算
- closed:定义区间的开闭,支持int类型的window。对于offset类型默认是左开右闭的即默认为right。可以根据情况指定为left both等。
举例1:对Series格式数据,滑动窗口设置为5
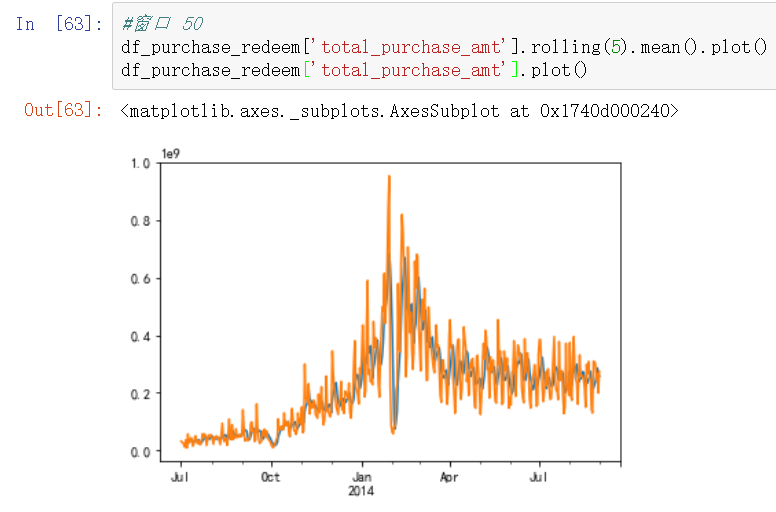
对DataFrame格式数据,滑动窗口设置为2
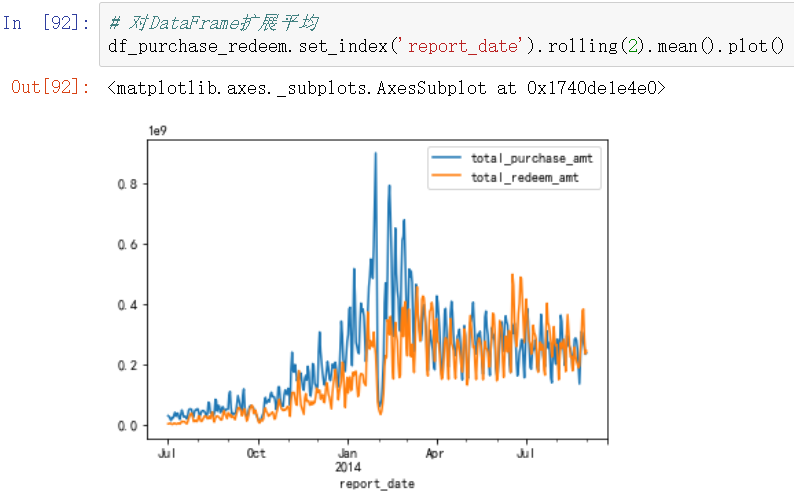
举例2:简单移动平均
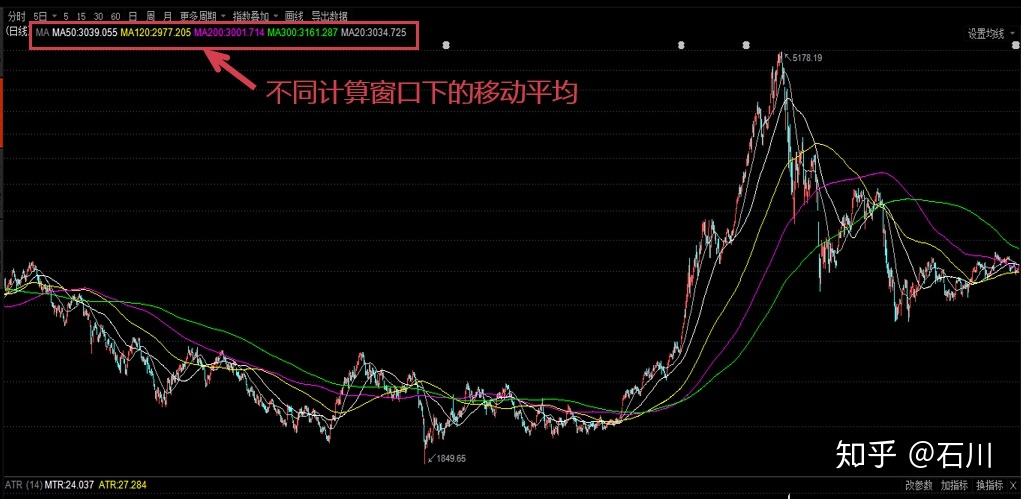
简单移动平均(Simple Moving Average, SMA)就是对时间序列直接求等权重均值,因此使用简单。但其最令人诟病的就是它的滞后性。从上图不难看出,随着计算窗口 的增大,移动平均线越来越平滑,但同时也越来越滞后。以 120 日均线为例,在 2015 年 6 月份之后的大熊市开始了很长一段时间之后,120 日均线才开始呈现下降趋势。如果我们按照这个趋势进行投资,那这个滞后无疑造成了巨额的亏损。
举例3:加权移动平均

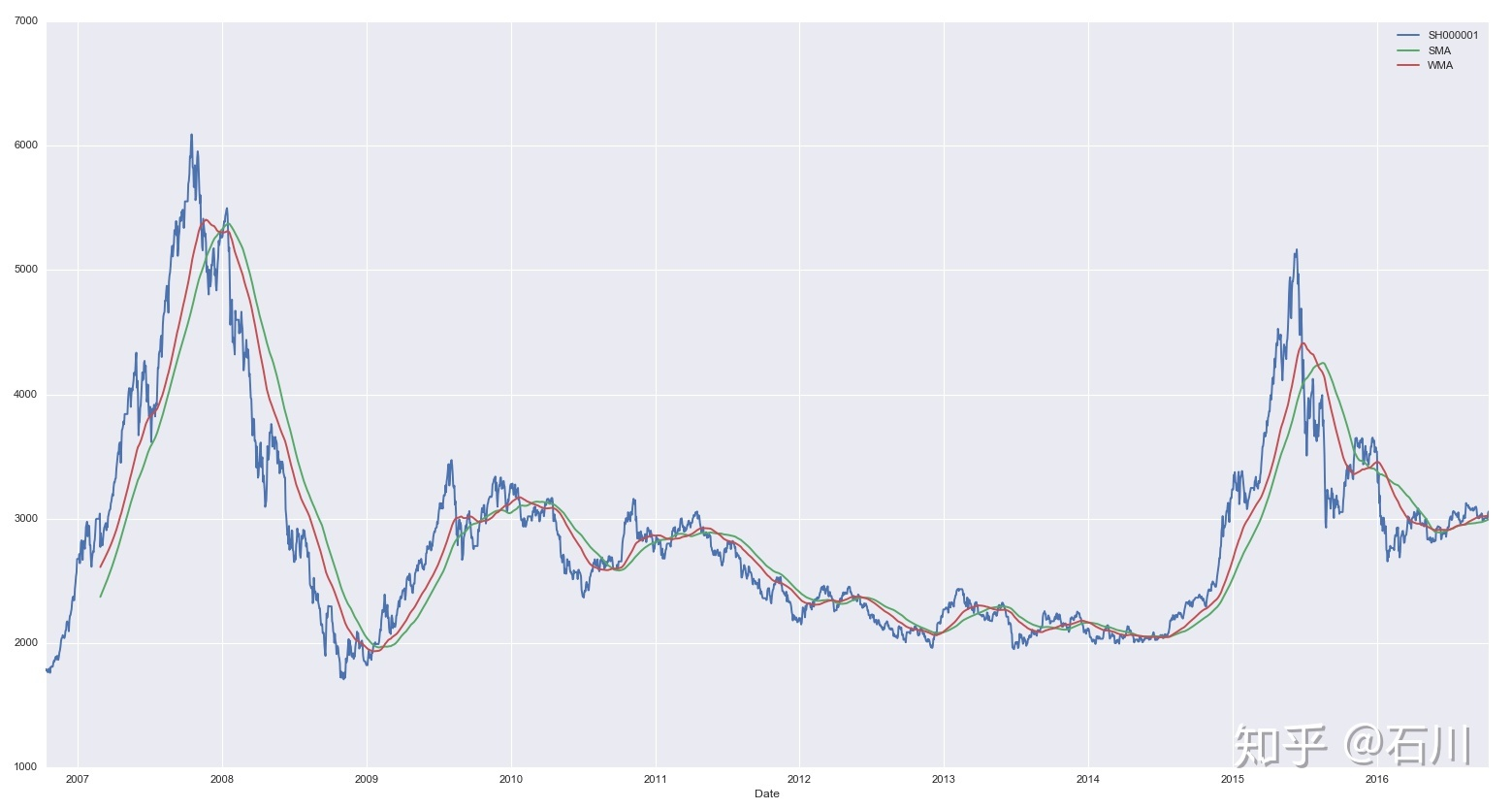
以上证指数过去 10 年的日数据为例,下图比较了 时的简单移动平均和加权移动平均的过滤效果。加权移动平均比简单移动平均对近期的变化更加敏感,尤其是在牛熊市转换的时候,加权移动平均的滞后性小于简单移动平均。但是,由于仅采用线性权重衰减,加权移动平均仍然呈现出滞后性。
2. 指数加权函数
使用固定大小窗口及相等权数观测值的办法是,定义一个衰减因子(decay factor)常量,以便使近期的观测值拥有更大的权重。

其中$alpha$表示权重的衰减程度,取值在 0 和 1 之间。$alpha$越大,过去的观测值衰减的越快。虽然指数移动平均是一个无穷级数,但在实际应用时,我们也经常看到T期指数移动平均的说法。这里的T是用来计算$alpha$的参数,它不表示指数衰减在 T 期后结束。 $alpha$和 T的关系为$alpha=2/(T+1)$ 。
下图比较了 $T=100$时简单移动平均、加权移动平均和指数移动平均的平滑效果。指数移动平均由于对近期的数据赋予了更高的权重,因此它比加权移动平均对近期的变化更加敏感,但这种效果在本例中并不显著,指数移动平均也存在一定的滞后。

当$alpha=1/T$时,得到的指数移动平均又称为修正移动平均(Modified Moving Average,MMA)或平滑移动平均(SMoothed Moving Average,SMMA),它们在应用中也十分常见。比如,在计算技术指标 ADX 的时候,就应用到了平滑移动平均。
无论是加权还是指数移动平均,它们都是通过对近期的数值赋予更高的权重来提高低频趋势对近期变化的敏感程度。然而,它们的计算表达式(或算法结构)是固定的,在整个时间序列上的各个时点都使用同样的结构(即一成不变的权重分配方法)计算移动平均,而不考虑时间序列自身的特点。
举例:简单移动平均与指数加权移动平均
#简单移动平均与指数加权移动平均
fig,axes = plt.subplots(nrows=2,ncols=1,sharex=True,sharey=True,figsize=(12,7))
total_purchase_amt_ = df_purchase_redeem.total_purchase_amt['2013-1':'2014-1']
ma20 = total_purchase_amt_.rolling(20,min_periods=10).mean()
ewma20 = pd.ewma(total_purchase_amt_,span=20,)
total_purchase_amt_.plot(style='k-',ax=axes[0])
ma20.plot(style='k--',ax=axes[0])
total_purchase_amt_.plot(style='k--',ax=axes[1])
ewma20.plot(style='k--',ax=axes[1])
axes[0].set_title('MA')
axes[1].set_title('指数加权 MA')

3. 二元移动窗口函数
有些统计运算(如相关系数和协方差)需要在两个时间序列上执行。例如,金融分析师常常对某只股票对某个参考指数(如标准普尔500指数)的相关系数感兴趣。我们可以通过计算百分数变化并使用rolling_corr的方式得到该结果。
pandas.rolling_corr(arg1, arg2=None, window=None, min_periods=None, freq=None, center=False, pairwise=None, how=None)

pct_change() #用于计算各种增长率,比如股市中的涨跌幅。计算变化率:(后一个值-前一个值)/前一个值
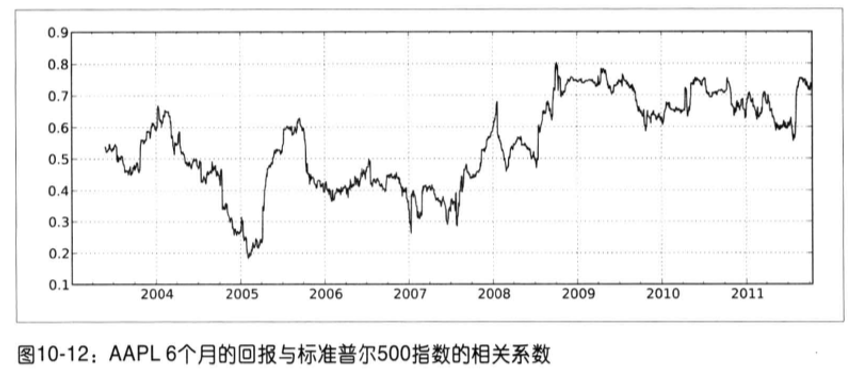
假设你想要一次性计算多只股票与标准普尔500指数的相关系数,需要传入一个TimeSeries和一个DataFrame各列的相关系数
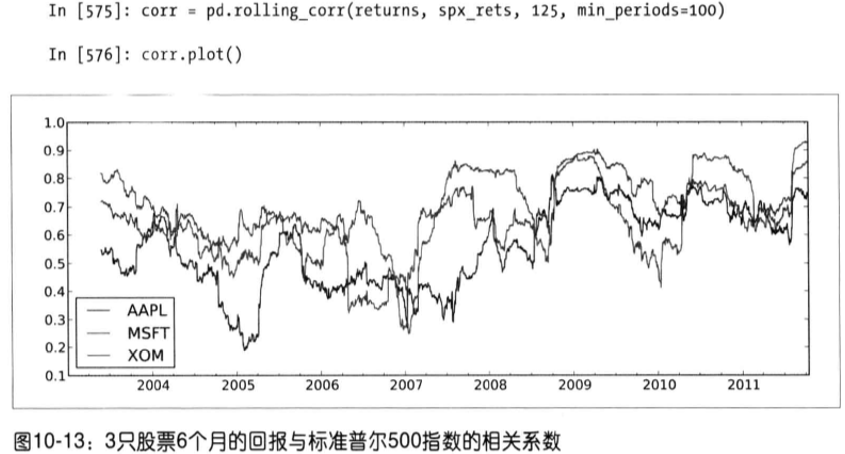
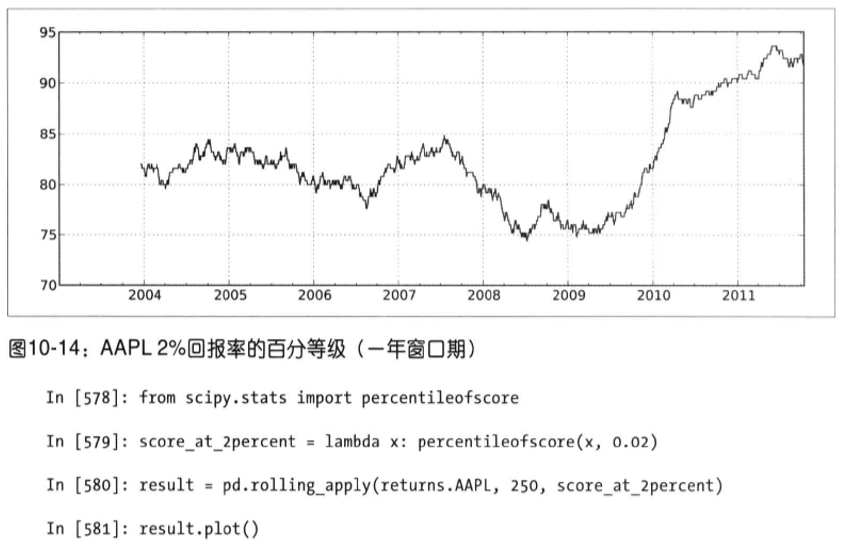
4. 用户自定义的移动窗口函数
通过rolling().apply()方法,可以在移动窗口上使用自己定义的函数。唯一需要满足的是,在数组的每一个片段上,函数必须产生单个值。
参考文献:
【2】Pandas —— cum累积计算和rolling滚动计算