1. 什么是Dropout(随机失活)
就是在神经网络的Dropout层,为每个神经元结点设置一个随机消除的概率,对于保留下来的神经元,我们得到一个节点较少,规模较小的网络进行训练。
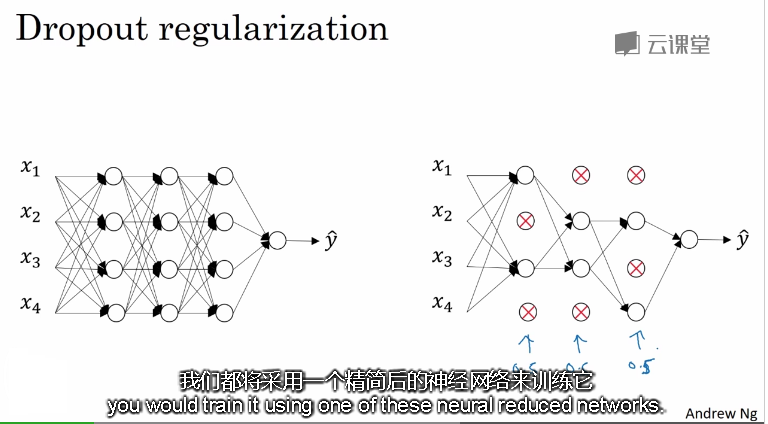
标准网络和dropout网络:
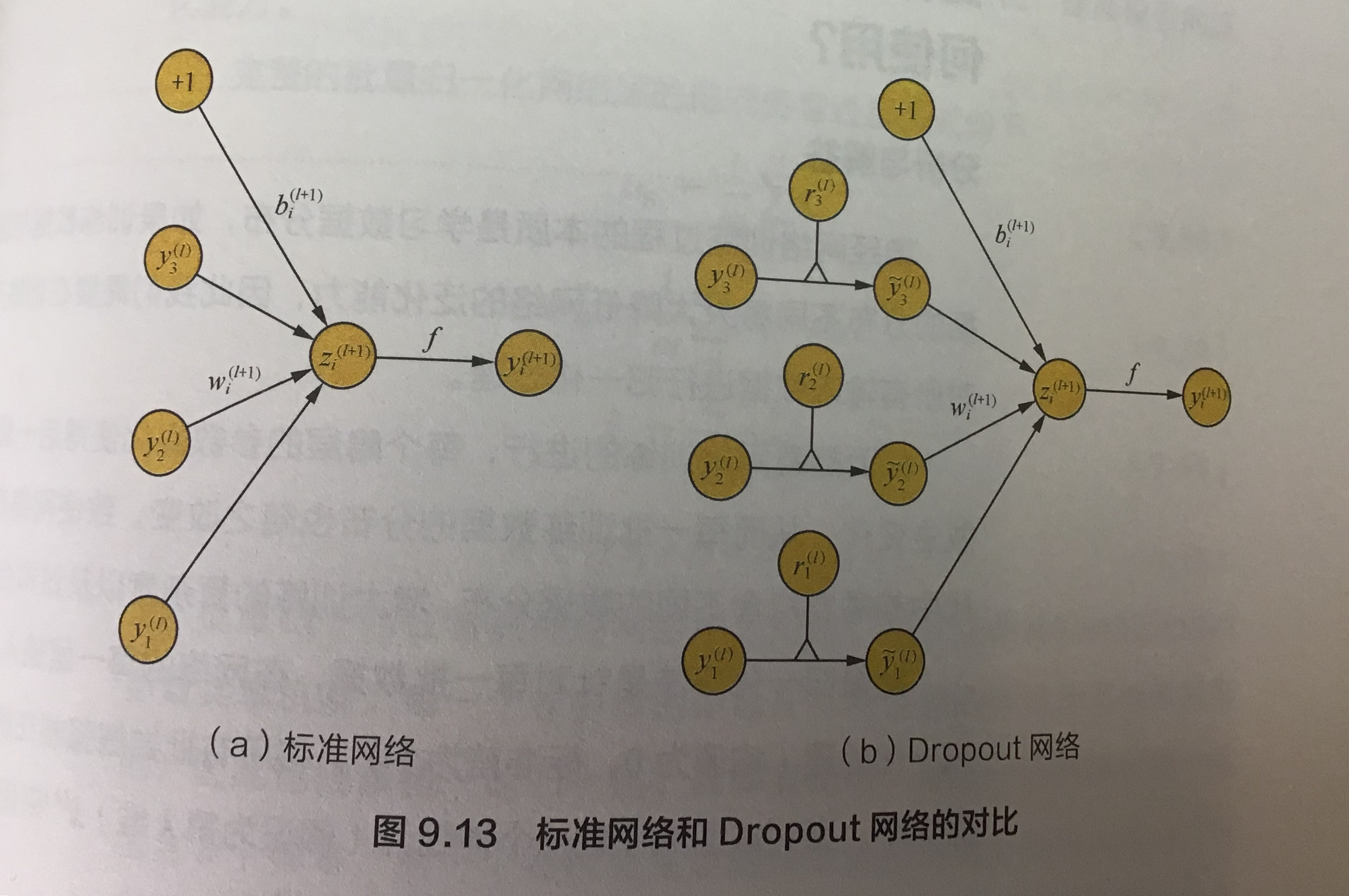
左边是简单的模型,右边是含有dropout的模型
l: hidden layer index (隐藏层索引)
z: denote the vector of inputs into layer l(表示l层的向量输入)
y: output of each layer(每一层的输出)
y0: input layer(输入层)
f: activation function(激活函数)
| 简单模型的输入输出的计算 | 含有dropout的模型,它在input layer 乘以伯努利随机概率,如果p =0.5,那么y就有50%的概率会变成0,这样它就不会参与运算 |
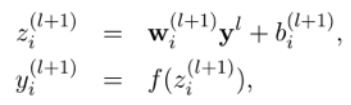 |

|
|
这个图表示的是不同的分类架构没有使用dropout和使用dropout有分类错误有显著的下降。 |
|
2.Dropout是如何防止过拟合的?

- 不依赖于任何一个特征,因为该单元的输入可能随时被清除
- 通过传播所有权重,dropout将产生收缩权重的平方范数的效果,和之前讲的L2正则化类似;
- 实施dropout的结果实它会压缩权重,并完成一些预防过拟合的外层正则化;
- L2对不同权重的衰减是不同的,它取决于激活函数倍增的大小。
3.怎么理解训练和测试的dropout不同?
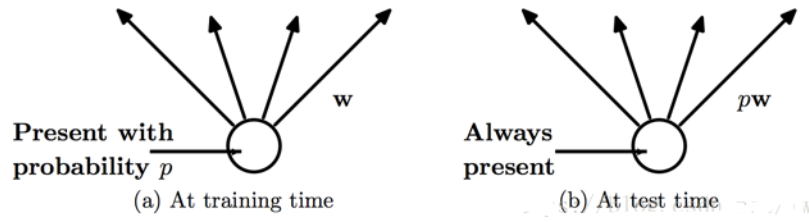
左边:在训练时,每个神经单元都可能以概率p去除。
右边:在测试阶段,每个神经元都是存在的,权重参数w要乘以p,成为pw。
左边我们应该比较好理解,每个神经元都有概率p参与单次神经网络的训练。而测试的时候,神经元是不会去除的,每个神经元都是存在的,权重参数w要乘以p。那么这里就产生一个问题,为什么参数w要乘以概率p。
-
问题:怎么理解测试时权重参数w要乘以概率p?
假设总共有100个神经元,训练的时候我们加上dropout,p=0.5,那么我们就有50个神经元参与训练,那么我们每次50个神经元训练出来的模型参数w是要比直接100个神经元要小的,因为它更新的次数会更少。我们测试的时候100个神经元是都会参与计算的,这就跟训练的时候我们使用50个神经元产生差异了,如果要保证测试的时候每个神经元的关联计算不能少,只能从通过改变w来达到跟训练时一样输出,所以才会有权重参数w乘以p。
4.实施dropout的细节
- 如果你担心某些层比其它层更容易发生过拟合,可以把某些层的keep-prob值设置得比其它层更低, 缺点是为了使用交叉验证,你要搜索更多的超级参数,
- 另一种方案是在一些层上应用dropout,而有些层不用dropout,应用dropout的层只含有一个超级参数,就是keep-prob。
训练:input 的dropout概率推荐是0.8(添加噪声);hidden layer 推荐是0.5(随机生成的网络结构最多)
测试:不需要dropout,但是需要将w乘以p,得到跟训练一样的输出
5.dropout常在计算机视觉应用中
- 计算视觉中的输入量非常大,输入太多像素,以至于没有足够的数据,所以dropout在计算机视觉中应用得比较频繁,有些计算机视觉研究人员非常喜欢用它,几乎成了默认的选择。
- 但要牢记一点,dropout是一种正则化方法,它有助于预防过拟合,除非算法过拟合,不然我是不会使用dropout的
- 它在其它领域应用得比较少,主要存在于计算机视觉领域,因为我们通常没有足够的数据,所以一直存在过拟合
6.dropout缺点
- dropout 的一大缺点是成本函数无法被明确定义。因为每次迭代都会随机消除一些神经元结点的影响,因此无法确保成本函数单调递减。因此,使用 dropout 时,先将keep_prob全部设置为 1.0 后运行代码,确保 J(w,b)函数单调递减,再打开 dropout
- 明显增加训练时间,因为引入dropout之后相当于每次只是训练的原先网络的一个子网络,为了达到同样的精度需要的训练次数会增多。dropout的缺点就在于训练时间是没有dropout网络的2-3倍
7.实现Dropout的方法
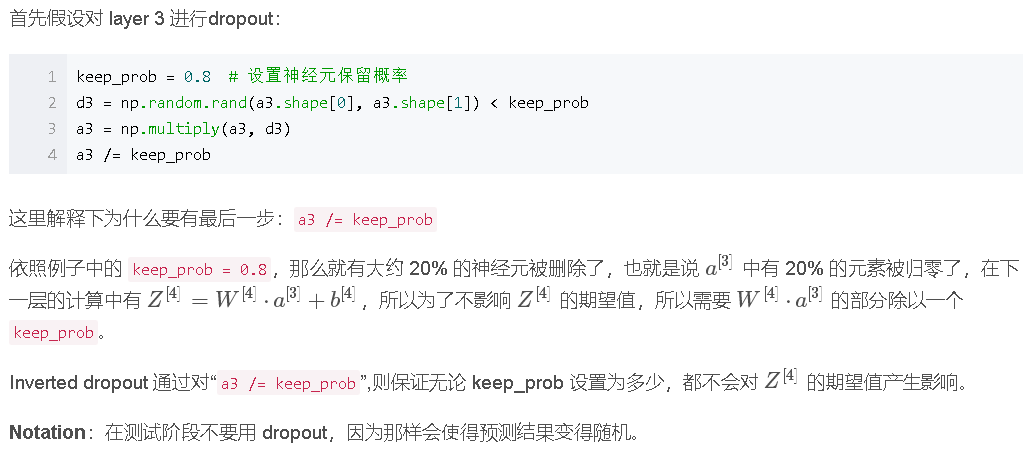
8.其他正则化方法
- 减小网络容量
参数更多的模型拥有更大的记忆容量,因此能够在训练样本和目标之间轻松的学会完美的字典式映射,这种映射没有任何泛化能力。
因此,为了让损失最小化,网络必须学会对目标具有很强预测能力的压缩表示。同时,使用的模型应该具有足够多的参数,防止欠拟合,即模型
避免记忆资源不足。在容量过大与容量不足之间要找到一个折中。
- 数据扩增(Data augmentation):通过图片的一些变换,得到更多的训练集和验证集;

- Early stopping:在交叉验证集的误差上升之前的点停止迭代,避免过拟合。这种方法的缺点是无法同时解决bias和variance之间的最优。

