一. 谱聚类概述
1、谱聚类
谱聚类是从图论中演化出来的算法,后来在聚类中得到了广泛的应用。它的主要思想是把所有的数据看做空间中的点,这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低,而距离较近的两个点之间的边权重值较高,通过对所有数据点组成的图进行切图,让切图后不同的子图间边权重和尽可能的低,而子图内的边权重和尽可能的高,从而达到聚类的目的。
2、谱聚类与k-means
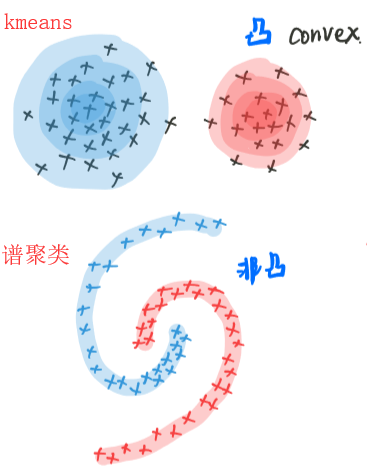
对比其他无监督聚类(如kmeans),spectral clustering的优点主要有以下:
- 过程对数据结构并没有太多的假设要求,如kmeans则要求数据为凸集。
- 可以通过构造稀疏similarity graph,使得对于更大的数据集表现出明显优于其他算法的计算速度
- 由于spectral clustering是对图切割处理,不会存在像kmeans聚类时将离散的小簇聚合在一起的情况。
- 无需像GMM一样对数据的概率分布做假设
同样,spectral clustering也有自己的缺点,主要存在于构图步骤,有如下:
- 对于选择不同的similarity graph比较敏感(如 epsilon-neighborhood, k-nearest neighborhood, full connected 等)
- 对于参数的选择也比较敏感(如epsilon-neighborhood的epsilon,k-nearest neighborhood的k)
二、谱聚类的推导
1、谱聚类的图模型
谱聚类过程主要有两步骤:第一步:构图 第二步:切图
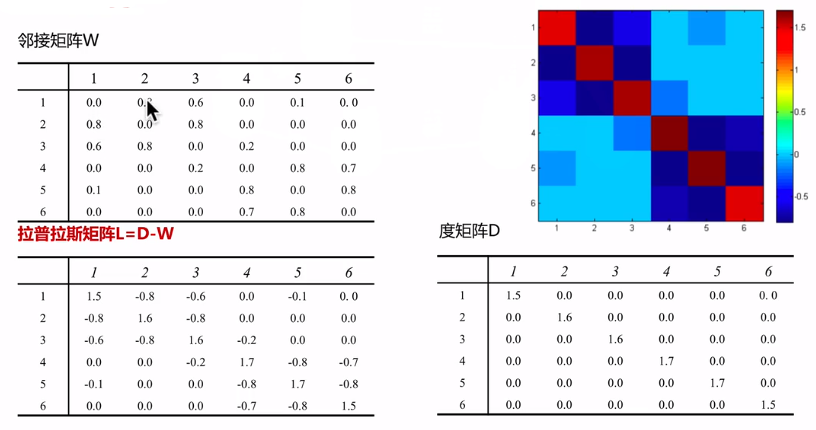
无向带权图模型G=<V,E>,每一条边上的权重wij为两个顶点的相似度,从而可以邻接矩阵W(或者称相似度矩阵),度矩阵D,从而有拉普拉斯矩阵L=D-W
如果点i和点j有邻边,就设置这条边的权重为核k(xi,xj)对应的值,wij=wji且wii=0,wij>=0
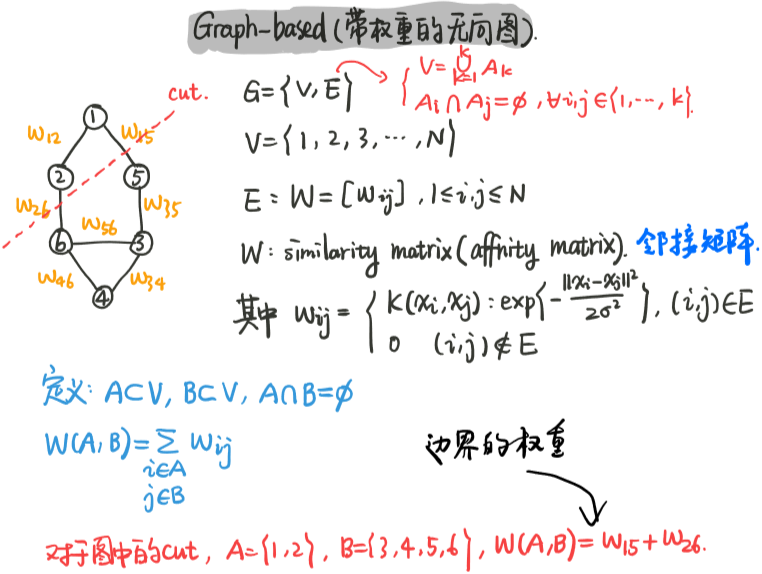
假设有k个类别,则需要切割的边就是所有类中的点到其他类点的权重之和,也就相当于所有类中的点到所有类中所有点的权重之和减去所有类中的所有点中的到该类中所有点的权重之和。
而我们的目标就是最小化这个所要切割的边的权重

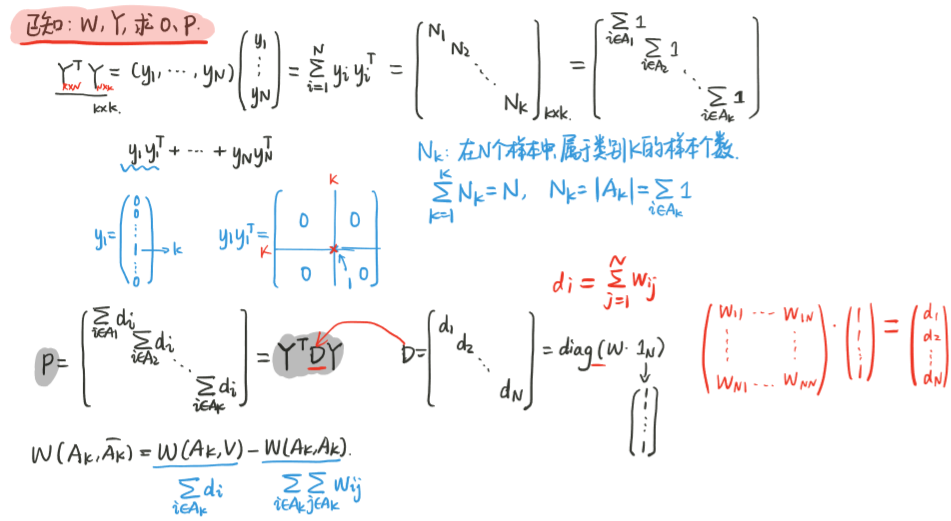
2、模型的矩阵形式--指示向量
尝试将目标的连加符号去掉,变成矩阵的形式,为此引入了指示向量Y,将Ncut转换成了矩阵的形式

3、模型的矩阵形式-对角矩阵

4、模型的矩阵形式-拉普拉斯矩阵

三、谱聚类的算法流程
1、算法流程

- 数据准备,生成图的邻接矩阵;
- 归一化拉普拉斯矩阵;
- 生成最小的k个特征值和对应的特征向量;
- 将特征向量kmeans聚类(少量的特征向量)
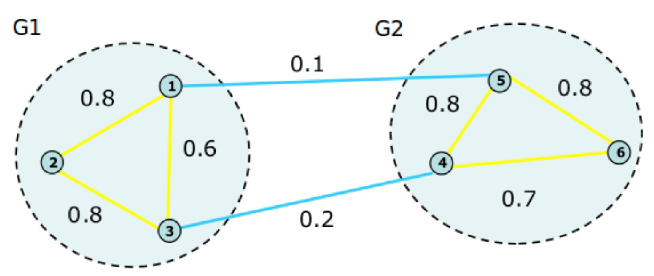
2、举例
计算权重矩阵W,如下图所示
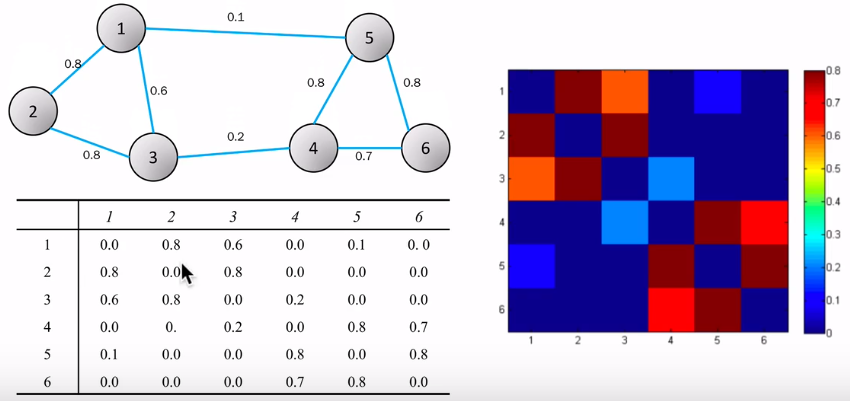
计算度矩阵D,如下图所示
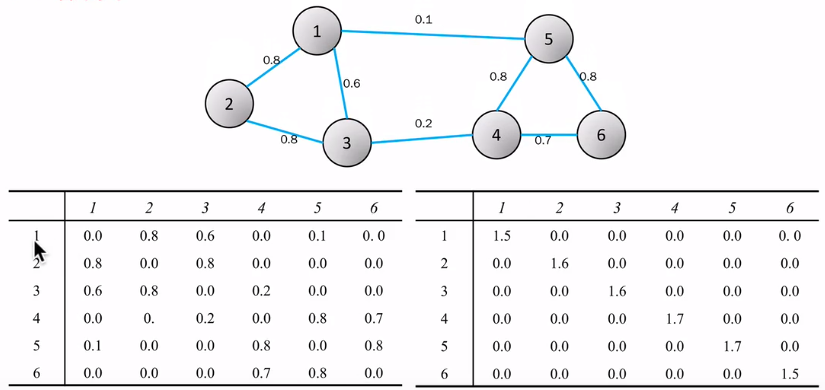
计算拉普拉斯矩阵L=D-W,如下图所示
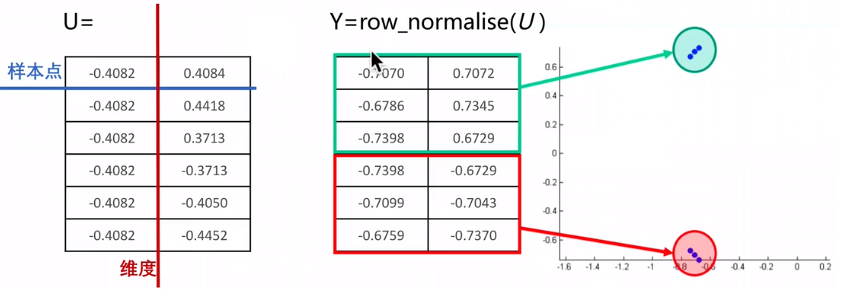
归一化拉普拉斯矩阵,并拉普拉斯矩阵的特征值,若k=2,就取前两个最小的特征值以及对应的特征向量,两个特征向量组成矩阵U,U就是降维之后的矩阵

U从横向看是6个样本点,纵向看是2个特征
对U归一化,得到了Y矩阵,用k-means可以形成两个聚类
四、谱聚类算法总结
谱聚类算法的主要优点有:
- 谱聚类只需要数据之间的相似度矩阵,因此对于处理稀疏数据的聚类很有效。这点传统聚类算法比如K-Means很难做到
- 由于使用了降维,因此在处理高维数据聚类时的复杂度比传统聚类算法好。
谱聚类算法的主要缺点有:
- 如果最终聚类的维度非常高,则由于降维的幅度不够,谱聚类的运行速度和最后的聚类效果均不好。
- k值只能靠猜测
- 聚类效果依赖于相似矩阵,不同的相似矩阵得到的最终聚类效果可能很不同。
- 划分不均衡

参考文献:
【1】谱聚类(spectral clustering)原理总结