参考url:
https://jakevdp.github.io/PythonDataScienceHandbook/05.05-naive-bayes.html
朴素贝叶斯模型是一组非常简单快速的分类算法,通常适用于维度非常高的数据集。
因为运行速度快,而且可调参数少,因此非常适合为分类问题提供快速粗糙的基本方案。
1、贝叶斯分类
朴素贝叶斯分类器建立在贝叶斯分类方法的基础上,其数学基础是贝叶斯定理(Bayes's theorem)——一个描述统计量条件概率关系的公式。
在贝叶斯分类中,将确定一个具有某些特征的样本属于某类标签的概率,记为P(L|特征)。

当需要确定两种标签,分别定义为L1和L2,一种方法就是计算这两个标签的后验概率的比值:
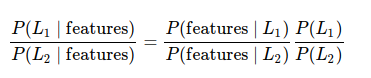
被称为'生成模型'的模型能够计算每个标签的P(特征|Li),它可以训练出,生成输入数据的假设随机过程(或称为概率分布)。
为每种标签设置生成模型是贝叶斯分类器训练过程的主要部分。
被称为'朴素'或'朴素贝叶斯',是因为如果对每种标签的生成模型进行非常简单的假设,就能找到每种类型生成模型的近似解,然后就可以使用贝叶斯分类。
不同类型的朴素贝叶斯分类器是由对数据的不同假设决定的。
2、高斯朴素贝叶斯
高斯朴素贝叶斯,这个分类器假设每个标签的数据都服从简单的高斯分布。
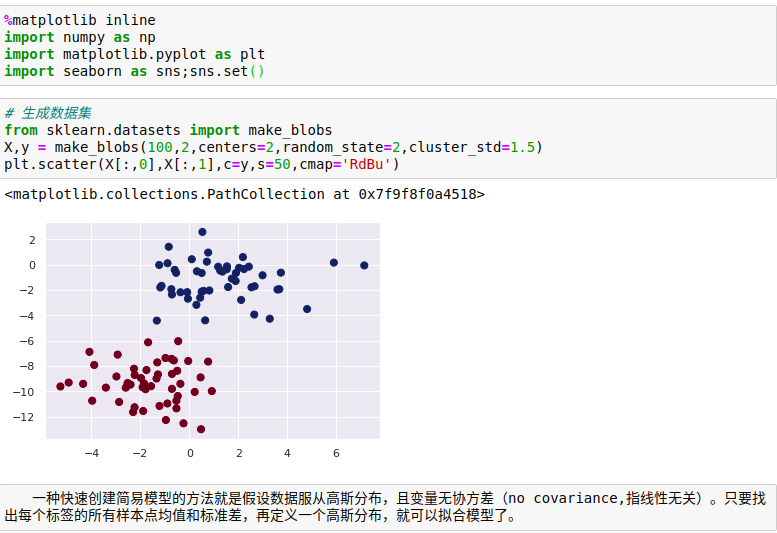
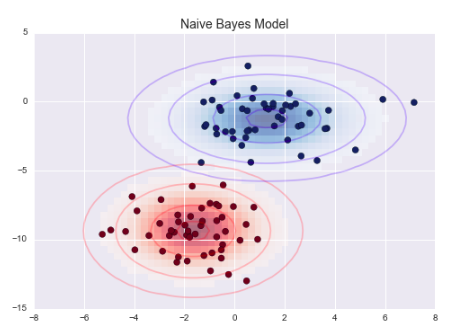
图中的椭圆曲线表示每个标签的高斯生成模型,越靠近椭圆中心的可能性越大。
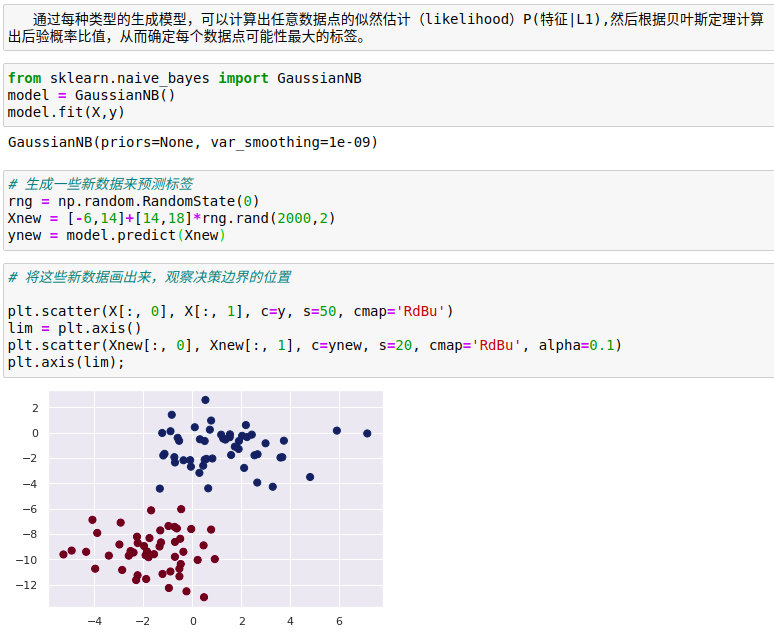
通常高斯朴素贝叶斯的边界是二次方曲线。
贝叶斯主义(Bayesian formalism)的一个优质特性是它天生支持概率分类,可以用predict_proba方法计算样本属于某个标签的概率:
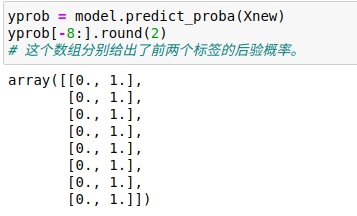
当需要评估分类器的不确定性,那么这类贝叶斯方法非常有用。
由于分类的最终效果只能依赖于一开始的模型假设,因此高斯朴素贝叶斯经常得不到非常好的结果。
3、多项式朴素贝叶斯
还有一种常用的假设是多项式朴素贝叶斯(multinomial naive Bayes),它假设特征是由一个简单多项式分布生成的。
多项式分布可以描述各种类型样本出现次数的概率,因此多项式朴素贝叶斯非常适合用于描述出现次数或者出现次数比例的特征。
多项式朴素贝叶斯通常用于文本分类,其特征都是指待分类文本的单词出现次数或者频率。
4、朴素贝叶斯的应用场景
朴素贝叶斯分类器对数据有严格的假设,因此其训练效果通过比复杂模型差。
其优点体现在四个方面,这些优点使得朴素贝叶斯分类器通常很适合作为分类的的初始解:
(1)训练和预测的速度非常快
(2)直接使用概率预测
(3)通常很容易解释
(4)可调参数非常少
朴素贝叶斯分类器非常适合用于以下应用场景:
(1)假设分布函数与数据匹配(实际中很少见)
(2)各种类型的区分度很高,模型复杂度不重要
(3)非常高维度的数据,模型复杂度不重要