欢迎探讨,如有错误敬请指正
如需转载,请注明出处http://www.cnblogs.com/nullzx/
1. 单轴快速排序的基本原理
快速排序的基本思想就是从一个数组中任意挑选一个元素(通常来说会选择最左边的元素)作为中轴元素,将剩下的元素以中轴元素作为比较的标准,将小于等于中轴元素的放到中轴元素的左边,将大于中轴元素的放到中轴元素的右边,然后以当前中轴元素的位置为界,将左半部分子数组和右半部分子数组看成两个新的数组,重复上述操作,直到子数组的元素个数小于等于1(因为一个元素的数组必定是有序的)。
以下的代码中会常常使用交换数组中两个元素值的Swap方法,其代码如下
public static void Swap(int[] A, int i, int j){
int tmp;
tmp = A[i];
A[i] = A[j];
A[j] = tmp;
}2. 快速排序中元素切分的方式
快速排序中最重要的就是步骤就是将小于等于中轴元素的放到中轴元素的左边,将大于中轴元素的放到中轴元素的右边,我们暂时把这个步骤定义为切分。而剩下的步骤就是进行递归而已,递归的边界条件为数组的元素个数小于等于1。以首元素作为中轴,看看常见的切分方式。
2.1 从两端扫描交换的方式
基本思想,使用两个变量i和j,i指向首元素的元素下一个元素(最左边的首元素为中轴元素),j指向最后一个元素,我们从前往后找,直到找到一个比中轴元素大的,然后从后往前找,直到找到一个比中轴元素小的,然后交换这两个元素,直到这两个变量交错(i > j)(注意不是相遇 i == j,因为相遇的元素还未和中轴元素比较)。最后对左半数组和右半数组重复上述操作。
public static void QuickSort1(int[] A, int L, int R){
if(L < R){//递归的边界条件,当 L == R时数组的元素个数为1个
int pivot = A[L];//最左边的元素作为中轴,L表示left, R表示right
int i = L+1, j = R;
//当i == j时,i和j同时指向的元素还没有与中轴元素判断,
//小于等于中轴元素,i++,大于中轴元素j--,
//当循环结束时,一定有i = j+1, 且i指向的元素大于中轴,j指向的元素小于等于中轴
while(i <= j){
while(i <= j && A[i] <= pivot){
i++;
}
while(i <= j && A[j] > pivot){
j--;
}
//当 i > j 时整个切分过程就应该停止了,不能进行交换操作
//这个可以改成 i < j, 这里 i 永远不会等于j, 因为有上述两个循环的作用
if(i <= j){
Swap(A, i, j);
i++;
j--;
}
}
//当循环结束时,j指向的元素是最后一个(从左边算起)小于等于中轴的元素
Swap(A, L, j);//将中轴元素和j所指的元素互换
QuickSort1(A, L, j-1);//递归左半部分
QuickSort1(A, j+1, R);//递归右半部分
}
}
2.2 两端扫描,一端挖坑,另一端填补
基本思想,使用两个变量i和j,i指向最左边的元素,j指向最右边的元素,我们将首元素作为中轴,将首元素复制到变量pivot中,这时我们可以将首元素i所在的位置看成一个坑,我们从j的位置从右向左扫描,找一个小于等于中轴的元素A[j],来填补A[i]这个坑,填补完成后,拿去填坑的元素所在的位置j又可以看做一个坑,这时我们在以i的位置从前往后找一个大于中轴的元素来填补A[j]这个新的坑,如此往复,直到i和j相遇(i == j,此时i和j指向同一个坑)。最后我们将中轴元素放到这个坑中。最后对左半数组和右半数组重复上述操作。
public static void QuickSort2(int[] A, int L, int R){
if(L < R){
//最左边的元素作为中轴复制到pivot,这时最左边的元素可以看做一个坑
int pivot = A[L];
//注意这里 i = L,而不是 i = L+1, 因为i代表坑的位置,当前坑的位置位于最左边
int i = L, j = R;
while(i < j){
//下面面两个循环的位置不能颠倒,因为第一次坑的位置在最左边
while(i < j && A[j] > pivot){
j--;
}
//填A[i]这个坑,填完后A[j]是个坑
//注意不能是A[i++] = A[j],当因i==j时跳出上面的循环时
//坑为i和j共同指向的位置,执行A[i++] = A[j],会导致i比j大1,
//但此时i并不能表示坑的位置
A[i] = A[j];
while(i < j && A[i] <= pivot){
i++;
}
//填A[j]这个坑,填完后A[i]是个坑,
//同理不能是A[j--] = A[i]
A[j] = A[i];
}
//循环结束后i和j相等,都指向坑的位置,将中轴填入到这个位置
A[i] = pivot;
QuickSort2(A, L, i-1);//递归左边的数组
QuickSort2(A, i+1, R);//递归右边的数组
}
}
2.3 单端扫描方式
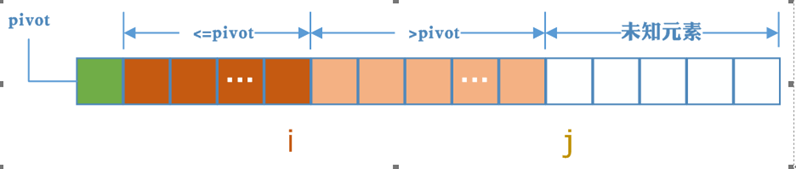
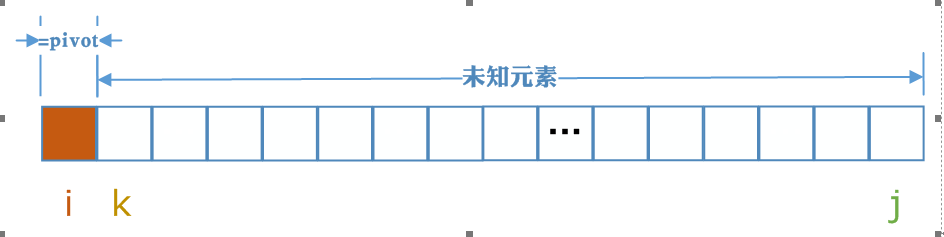
j从左向右扫描,A[1,i]表示小于等于pivot的部分,A[i+1,j-1]表示大于pivot的部分,A[j, R]表示未知元素
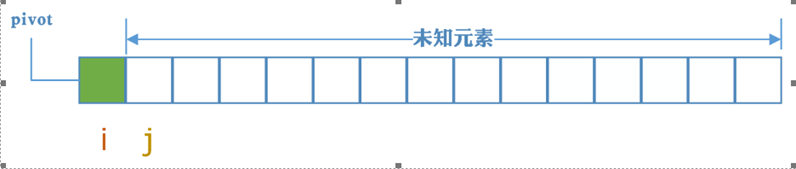
初始化时,选取最左边的元素作为中轴元素,A[1,i]表示小于等于pivot的部分,i指向中轴元素(i < 1),表示小于等于pivot的元素个数为0,j以后的都是未知元素(即不知道比pivot大,还是比中轴元素小),j初始化指向第一个未知元素。
当A[j]大于pivot时,j继续向前,此时大于pivot的部分就增加一个元素
上图中假设对A[j]与pivot比较后发现A[j]大于pivot时,j的变化
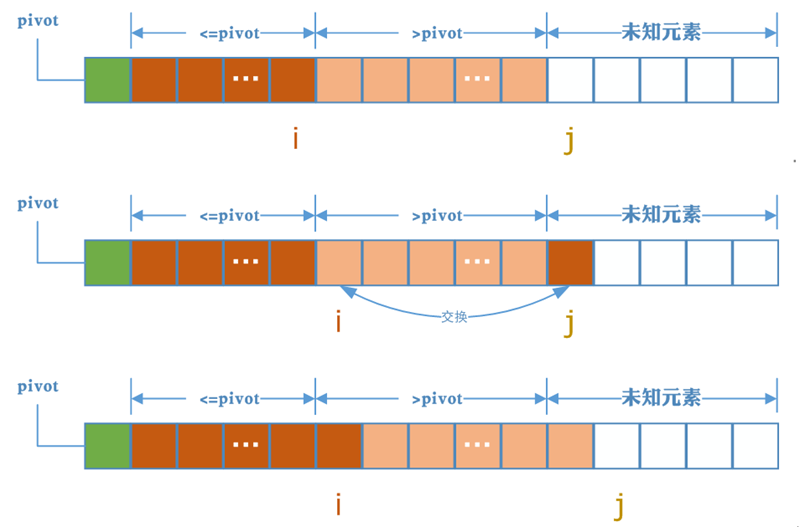
当A[j]小于等于pivot时,我们注意注意i的位置,i的下一个就是大于pivot的元素,我们将i增加1然后交换A[i]和A[j],交换后小于等于pivot的部分增加1,j增加1,继续扫描下一个。而i的下一个元素仍然大于pivot,又回到了先前的状态。
上图中假设对A[j]与pivot比较后发现A[j] <= pivot时,i,j的变化
public static void QuickSort3(int[] A, int L, int R){
if(L < R){
int pivot = A[L];//最左边的元素作为中轴元素
//初始化时小于等于pivot的部分,元素个数为0
//大于pivot的部分,元素个数也为0
int i = L, j = L+1;
while(j <= R){
if(A[j] <= pivot){
i++;
Swap(A, i, j);
j++;//j继续向前,扫描下一个
}else{
j++;//大于pivot的元素增加一个
}
}
//A[i]及A[i]以前的都小于等于pivot
//循环结束后A[i+1]及它以后的都大于pivot
//所以交换A[L]和A[i],这样我们就将中轴元素放到了适当的位置
Swap(A, L, i);
QuickSort3(A, L, i-1);
QuickSort3(A, i+1, R);
}
}
3. 三向切分的快速排序
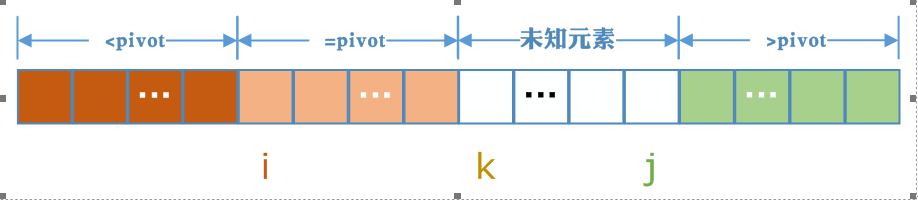
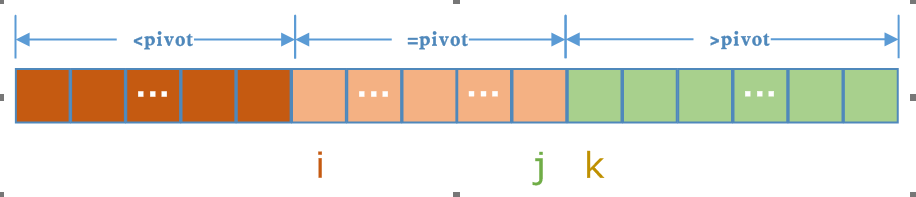
三向切分快速排序的基本思想,用i,j,k三个将数组切分成四部分,a[L, i-1]表示小于pivot的部分,a[i, k-1]表示等于pivot的部分,a[j+1]表示大于pivot的部分,而a[k, j]表示未判定的元素(即不知道比pivot大,还是比中轴元素小)。我们要注意a[i]始终位于等于pivot部分的第一个元素,a[i]的左边是小于pivot的部分。
我们选取最左边的元素作为中轴元素,初始化时,i = L,k = L+1,j=R(L表示最左边元素的索引,R表示最右边元素的索引)
通过上一段的表述可知,初始化时<pivot部分的元素个数为0,等于pivot部分元素的个数为1,大于pivot部分的元素个数为0,这显然符合目前我们对所掌握的情况。k自左向右扫描直到k与j错过为止(k > j)。我们扫描的目的就是逐个减少未知元素,并将每个元素按照和pivot的大小关系放到不同的区间上去。
在k的扫描过程中我们可以对a[k]分为三种情况讨论
(1)a[k] < pivot 交换a[i]和a[k],然后i和k都自增1,k继续扫描
(2)a[k] = pivot k自增1,k接着继续扫描
(3)a[k] > pivot 这个时候显然a[k]应该放到最右端,大于pivot的部分。但是我们不能直接将a[k]与a[j]交换,因为目前a[j]和pivot的关系未知,所以我们这个时候应该从j的位置自右向左扫描。而a[j]与pivot的关系可以继续分为三种情况讨论
3.1)a[j] > pivot j自减1,j接着继续扫描
3.2)a[j] == pivot 交换a[k]和a[j],k自增1,j自减1,k继续扫描(注意此时j的扫描就结束了)
3.3)a[j] < pivot: 此时我们注意到a[j] < pivot, a[k] > pivot, a[i] == pivot,那么我们只需要将a[j]放到a[i]上,a[k]放到a[j]上,而a[i]放到a[k]上。然后i和k自增1,j自减1,k继续扫描(注意此时j的扫描就结束了)
注意,当扫描结束时,i和j的表示了=等于pivot部分的起始位置和结束位置。我们只需要对小于pivot的部分以及大于pivot的部分重复上述操作即可。
public static void QuickSort3Way(int[] A, int L, int R){
if(L >= R){//递归终止条件,少于等于一个元素的数组已有序
return;
}
int i,j,k,pivot;
pivot = A[L]; //首元素作为中轴
i = L;
k = L+1;
j = R;
OUT_LOOP:
while(k <= j){
if(A[k] < pivot){
Swap(A, i, k);
i++;
k++;
}else
if(A[k] == pivot){
k++;
}else{// 遇到A[k]>pivot的情况,j从右向左扫描
while(A[j] > pivot){//A[j]>pivot的情况,j继续向左扫描
j--;
if(j < k){
break OUT_LOOP;
}
}
if(A[j] == pivot){//A[j]==pivot的情况
Swap(A, k, j);
k++;
j--;
}else{//A[j]<pivot的情况
Swap(A, i, j);
Swap(A, j, k);
i++;
k++;
j--;
}
}
}
//A[i, j] 等于 pivot 且位置固定,不需要参与排序
QuickSort3Way(A, L, i-1); // 对小于pivot的部分进行递归
QuickSort3Way(A, j+1, R); // 对大于pivot的部分进行递归
} 4. 双轴快速排序
双轴快速排序算法思路和三向切分快速排序算法的思路基本一致,双轴快速排序算法使用两个轴,通常选取最左边的元素作为pivot1和最右边的元素作pivot2。首先要比较这两个轴的大小,如果pivot1 > pivot2,则交换最左边的元素和最右边的元素,已保证pivot1 <= pivot2。双轴快速排序同样使用i,j,k三个变量将数组分成四部分
A[L+1, i]是小于pivot1的部分,A[i+1, k-1]是大于等于pivot1且小于等于pivot2的部分,A[j, R]是大于pivot2的部分,而A[k, j-1]是未知部分。和三向切分的快速排序算法一样,初始化i = L,k = L+1,j=R,k自左向右扫描直到k与j相交为止(k == j)。我们扫描的目的就是逐个减少未知元素,并将每个元素按照和pivot1和pivot2的大小关系放到不同的区间上去。
在k的扫描过程中我们可以对a[k]分为三种情况讨论(注意我们始终保持最左边和最右边的元素,即双轴,不发生交换)
(1)a[k] < pivot1 i先自增,交换a[i]和a[k],k自增1,k接着继续扫描
(2)a[k] >= pivot1 && a[k] <= pivot2 k自增1,k接着继续扫描
(3)a[k] > pivot2: 这个时候显然a[k]应该放到最右端大于pivot2的部分。但此时,我们不能直接将a[k]与j的下一个位置a[--j]交换(可以认为A[j]与pivot1和pivot2的大小关系在上一次j自右向左的扫描过程中就已经确定了,这样做主要是j首次扫描时避免pivot2参与其中),因为目前a[--j]和pivot1以及pivot2的关系未知,所以我们这个时候应该从j的下一个位置(--j)自右向左扫描。而a[--j]与pivot1和pivot2的关系可以继续分为三种情况讨论
3.1)a[--j] > pivot2 j接着继续扫描
3.2)a[--j] >= pivot1且a[j] <= pivot2 交换a[k]和a[j],k自增1,k继续扫描(注意此时j的扫描就结束了)
3.3) a[--j] < pivot1 先将i自增1,此时我们注意到a[j] < pivot1, a[k] > pivot2, pivot1 <= a[i] <=pivot2,那么我们只需要将a[j]放到a[i]上,a[k]放到a[j]上,而a[i]放到a[k]上。k自增1,然后k继续扫描(此时j的扫描就结束了)
注意
1. pivot1和pivot2在始终不参与k,j扫描过程。
2. 扫描结束时,A[i]表示了小于pivot1部分的最后一个元素,A[j]表示了大于pivot2的第一个元素,这时我们只需要交换pivot1(即A[L])和A[i],交换pivot2(即A[R])与A[j],同时我们可以确定A[i]和A[j]所在的位置在后续的排序过程中不会发生变化(这一步非常重要,否则可能引起无限递归导致的栈溢出),最后我们只需要对A[L, i-1],A[i+1, j-1],A[j+1, R]这三个部分继续递归上述操作即可。
public static void QuickSortDualPivot(int[] A, int L, int R){
if(L >= R){
return;
}
if(A[L] > A[R]){
Swap(A, L, R); //保证pivot1 <= pivot2
}
int pivot1 = A[L];
int pivot2 = A[R];
//如果这样初始化 i = L+1, k = L+1, j = R-1,也可以
//但代码中边界条件, i,j先增减,循环截止条件,递归区间的边界都要发生相应的改变
int i = L;
int k = L+1;
int j = R;
OUT_LOOP:
while(k < j){
if(A[k] < pivot1){
i++;//i先增加,首次运行pivot1就不会发生改变
Swap(A, i, k);
k++;
}else
if(A[k] >= pivot1 && A[k] <= pivot2){
k++;
}else{
while(A[--j] > pivot2){//j先增减,首次运行pivot2就不会发生改变
if(j <= k){//当k和j相遇
break OUT_LOOP;
}
}
if(A[j] >= pivot1 && A[j] <= pivot2){
Swap(A, k, j);
k++;
}else{
i++;
Swap(A, j, k);
Swap(A, i, k);
k++;
}
}
}
Swap(A, L, i);//将pivot1交换到适当位置
Swap(A, R, j);//将pivot2交换到适当位置
//一次双轴切分至少确定两个元素的位置,这两个元素将整个数组区间分成三份
QuickSortDualPivot(A, L, i-1);
QuickSortDualPivot(A, i+1, j-1);
QuickSortDualPivot(A, j+1, R);
}
下面代码初始化方式使得边界条件更加容易确定,在下面代码的方式中A[L+1]~A[i-1]表示小于pivot1的部分,A[i]~A[j]表示两轴之间的部分,A[j]~A[R-1]表示大于pivot2的部分。
当排序数组中不存在pivot1~pivot2中的部分时,一趟交换完成后i恰好比j大1;当排序数组中仅仅存在一个元素x使得pivot1 <=x <=pivot2时,一趟交换完成,i和j恰好相等。
public static void QuickSortDualPivot(int[] A, int L, int R){
if(L >= R){
return;
}
if(A[L] > A[R]){
Swap(A, L, R); //保证pivot1 <= pivot2
}
int pivot1 = A[L];
int pivot2 = A[R];
int i = L+1;
int k = L+1;
int j = R-1;
OUT_LOOP:
while(k <= j){
if(A[k] < pivot1){
Swap(A, i, k);
k++;
i++;
}else
if(A[k] >= pivot1 && A[k] <= pivot2){
k++;
}else{
while(A[j] > pivot2){
j--;
if(j < k){//当k和j错过
break OUT_LOOP;
}
}
if(A[j] >= pivot1 && A[j] <= pivot2){
Swap(A, k, j);
k++;
j--;
}else{//A[j] < pivot1
Swap(A, j, k);//注意k不动
j--;
}
}
}
i--;
j++;
Swap(A, L, i);//将pivot1交换到适当位置
Swap(A, R, j);//将pivot2交换到适当位置
//一次双轴切分至少确定两个元素的位置,这两个元素将整个数组区间分成三份
QuickSortDualPivot(A, L, i-1);
QuickSortDualPivot(A, i+1, j-1);
QuickSortDualPivot(A, j+1, R);
}补上一个单元测试
package test;
import java.util.Arrays;
import static datastruct.QuickSortForInt.*;
import org.junit.Assert;
import org.junit.Test;
public class QuickSortForIntTest {
@Test
public void testQuickSortDualPivot() {
int[] a;
int[] r;
a = new int[]{1};
r = a.clone();
QuickSortDualPivot(a, 0, a.length-1);
Arrays.sort(r);
Assert.assertArrayEquals(a, r);
a = new int[]{2, 1};
r = a.clone();
QuickSortDualPivot(a, 0, a.length-1);
Arrays.sort(r);
Assert.assertArrayEquals(a, r);
a = new int[]{1, 1};
r = a.clone();
QuickSortDualPivot(a, 0, a.length-1);
Arrays.sort(r);
Assert.assertArrayEquals(a, r);
a = new int[]{1, 1, 1};
r = a.clone();
QuickSortDualPivot(a, 0, a.length-1);
Arrays.sort(r);
Assert.assertArrayEquals(a, r);
a = new int[]{2, 1, 2};
r = a.clone();
QuickSortDualPivot(a, 0, a.length-1);
Arrays.sort(r);
Assert.assertArrayEquals(a, r);
a = new int[]{1, 2, 3};
r = a.clone();
QuickSortDualPivot(a, 0, a.length-1);
Arrays.sort(r);
Assert.assertArrayEquals(a, r);
a = new int[]{3, 2, 1};
r = a.clone();
QuickSortDualPivot(a, 0, a.length-1);
Arrays.sort(r);
Assert.assertArrayEquals(a, r);
/*pivot1 = 3, pivot2 = 5, 而且没有3~5之间的元素*/
a = new int[]{3, 1, 6, 2, 7, 5};
r = a.clone();
QuickSortDualPivot(a, 0, a.length-1);
Arrays.sort(r);
Assert.assertArrayEquals(a, r);
/*pivot1 = 3, pivot2 = 5, 只有一个元素4在3到5之间*/
a = new int[]{3, 1, 6, 4, 7, 5};
r = a.clone();
QuickSortDualPivot(a, 0, a.length-1);
Arrays.sort(r);
Assert.assertArrayEquals(a, r);
/*pivot1 = 3, pivot2 = 5, 所有元素都大于5*/
a = new int[]{3, 6, 7, 5};
r = a.clone();
QuickSortDualPivot(a, 0, a.length-1);
Arrays.sort(r);
Assert.assertArrayEquals(a, r);
/*pivot1 = 3, pivot2 = 5, 所有元素都小于3*/
a = new int[]{5, 2, 1, 3};
r = a.clone();
QuickSortDualPivot(a, 0, a.length-1);
Arrays.sort(r);
Assert.assertArrayEquals(a, r);
}
}
5. 参考文章
[1] 算法(第四版)RobertSedgewick