P4196 [CQOI2006]凸多边形

题目描述

逆时针给出n个凸多边形的顶点坐标，求它们交的面积。例如n=2时，两个凸多边形如下图：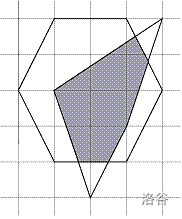 

则相交部分的面积为5.233。

输入格式

第一行有一个整数n，表示凸多边形的个数，以下依次描述各个多边形。第i个多边形的第一行包含一个整数mi，表示多边形的边数，以下mi行每行两个整数，逆时针给出各个顶点的坐标。

输出格式

输出文件仅包含一个实数，表示相交部分的面积，保留三位小数。

输入输出样例

输入 #1

2

6

-2 0

-1 -2

1 -2

2 0

1 2

-1 2

4

0 -3

1 -1

2 2

-1 0

输出 #1

5.233

说明/提示

100%的数据满足：2<=n<=10，3<=mi<=50，每维坐标为[-1000,1000]内的整数

#include<bits/stdc++.h>//求凸多边形面积

#define ll long long
using namespace std;
const int N = 1100;
int n, cnt, tot;
double ans;
struct P {
    double x, y;
} p[N], a[N];
struct L {
    P a, b;
    double val;//atan2

} l[N], q[N];

P operator-(P a, P b) {
    P t;
    t.x = a.x - b.x;
    t.y = a.y - b.y;
    return t;
}

double operator*(P a, P b) {// 叉积
    return a.x * b.y - a.y * b.x;
}

bool operator<(L a, L b) {//极角排序
    if (a.val != b.val)return a.val < b.val;// 角度
    return (a.b - a.a) * (b.b - a.a) > 0;//通过叉积的正向性来判断相同角度的向量,极角小的排在前
}

P inter(L a, L b) {//求两直线的交点
    double k1, k2, t;
    k1 = (b.b - a.a) * (a.b - a.a);
    k2 = (a.b - a.a) * (b.a - a.a);
    t = k1 / (k1 + k2);
    P ans;
    ans.x = b.b.x + (b.a.x - b.b.x) * t;
    ans.y = b.b.y + (b.a.y - b.b.y) * t;
    return ans;
}

bool check(L a, L b, L t) {//判断该直线是否对队首或队尾元素有影响
    P p = inter(a, b);//前两条直线的交点
    return (t.b - t.a) * (p - t.a) < 0;//如果该直线的极角比交点的大,则弹出该元素
}

void hpi() {//半平面交
    sort(l + 1, l + cnt + 1);//极角排序
    int L = 1, R = 0;
    tot = 0;
    for (int i = 1; i <= cnt; i++) {
        if (l[i].val != l[i - 1].val)tot++;
        l[tot] = l[i];//斜率相同的优先取极角大的，因为是逆时针
    }
    cnt = tot;
    tot = 0;
    q[++R] = l[1];//单调队列
    q[++R] = l[2];
    for (int i = 3; i <= cnt; i++) {
        while (L < R && check(q[R - 1], q[R], l[i]))R--;//先判断队尾
        while (L < R && check(q[L + 1], q[L], l[i]))L++;//后判断队首
        q[++R] = l[i];// 元素入队
    }
    while (L < R && check(q[R - 1], q[R], q[L]))R--;//最后用队首的向量排除一下队尾多余的向量
    while (L < R && check(q[L + 1], q[L], q[R]))L++;
    q[R + 1] = q[L];
    for (int i = L; i <= R; i++)
        a[++tot] = inter(q[i], q[i + 1]);
}

void getans() {// 求凸包面积
    if (tot < 3)return;
    a[++tot] = a[1];
    for (int i = 1; i <= tot; i++)
        ans += a[i] * a[i + 1];
    ans = fabs(ans) / 2;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin >> n;
    for (int i = 1; i <= n; i++) {
        int k;
        cin >> k;
        for (int j = 1; j <= k; j++)
            cin >> p[j].x >> p[j].y;
        p[k + 1] = p[1];
        for (int j = 1; j <= k; j++)
            l[++cnt].a = p[j], l[cnt].b = p[j + 1];//存成直线
    }
    for (int i = 1; i <= cnt; i++)
        l[i].val = atan2(l[i].b.y - l[i].a.y, l[i].b.x - l[i].a.x);
    hpi();
    getans();
    cout << fixed << setprecision(3) << ans << endl;
    return 0;
}