Problem Codeforces #541 (Div2) - E. String Multiplication
Time Limit: 2000 mSec
![]() Problem Description
Problem Description

Input
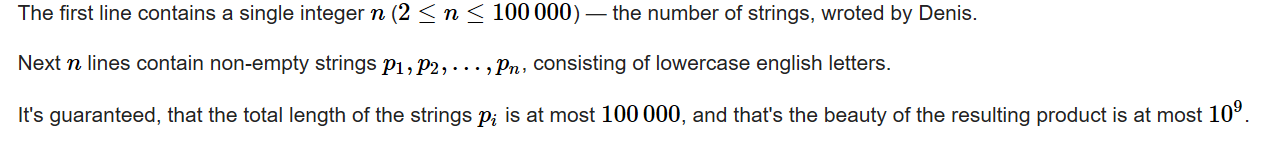
![]() Output
Output
Print exactly one integer — the beauty of the product of the strings.
![]() Sample Input
Sample Input
3
a
b
a
![]() Sample Output
Sample Output
3
题解:这个题的思维难度其实不大,需要维护什么东西很容易想到,或者说套路十分明显
1、字符串无限制条件下最大值
2、强制选择左端点/右端点的最大值
3、是否只有一种字符
基本上需要维护的量就是这些,不过写起来实在是非常麻烦,以我的代码能力短时间实在是写不出来,后来参考了一位大佬的代码,写的思路清晰,代码简洁,实在是非常值得学习,之所以能够使得代码变简洁,主要是因为他枚举了字母。题目明确说明只有小写英文字母,所以最后的最大值无非就是这26个字母中的一个形成的,因此分别计算各个字母对应的最大值即可算出最终最大值,而一旦固定了每次考虑取最大值的字母,写代码的难度会大大降低,关键点就这一条,直接上代码。
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define REP(i, n) for (int i = 1; i <= (n); i++) 6 #define sqr(x) ((x) * (x)) 7 8 const int maxn = 100000 + 100; 9 const int maxm = 200000 + 100; 10 const int maxs = 10000 + 10; 11 12 typedef long long LL; 13 typedef pair<int, int> pii; 14 typedef pair<double, double> pdd; 15 16 const LL unit = 1LL; 17 const int INF = 0x3f3f3f3f; 18 const LL mod = 1000000007; 19 const double eps = 1e-14; 20 const double inf = 1e15; 21 const double pi = acos(-1.0); 22 23 int n; 24 int len[maxn]; 25 string str[maxn]; 26 27 int main() 28 { 29 ios::sync_with_stdio(false); 30 cin.tie(0); 31 //freopen("input.txt", "r", stdin); 32 //freopen("output.txt", "w", stdout); 33 cin >> n; 34 for (int i = 1; i <= n; i++) 35 { 36 cin >> str[i]; 37 len[i] = str[i].size(); 38 } 39 int ans = 0; 40 for (int c = 0; c < 26; c++) 41 { 42 int mx = 0, cnt = 0; 43 for (int i = 0; i < len[1]; i++) 44 { 45 if (str[1][i] - 'a' != c) 46 { 47 mx = max(mx, cnt); 48 cnt = 0; 49 } 50 else 51 { 52 cnt++; 53 } 54 } 55 mx = max(mx, cnt); 56 for (int i = 2; i <= n; i++) 57 { 58 int lmx = 0, rmx = 0; 59 int nmx = 0; 60 for (int j = 0; j < len[i]; j++) 61 { 62 if (str[i][j] - 'a' == c) 63 lmx++; 64 else 65 break; 66 } 67 for (int j = len[i] - 1; j >= 0; j--) 68 { 69 if (str[i][j] - 'a' == c) 70 rmx++; 71 else 72 break; 73 } 74 cnt = 0; 75 for (int j = 0; j < len[i]; j++) 76 { 77 if (str[i][j] - 'a' != c) 78 { 79 nmx = max(nmx, cnt); 80 cnt = 0; 81 } 82 else 83 cnt++; 84 } 85 nmx = max(nmx, cnt); 86 87 if (nmx == len[i]) 88 { 89 mx = (mx + 1) * nmx + mx; 90 } 91 else 92 { 93 if (mx != 0) 94 mx = lmx + rmx + 1; 95 else 96 mx = max(lmx, rmx); 97 } 98 mx = max(mx, nmx); 99 } 100 ans = max(ans, mx); 101 } 102 cout << ans << endl; 103 return 0; 104 }