【概率论与数理统计】全概率公式和贝叶斯公式

1. 条件概率公式

---

设A, B是两个事件，且P(B)>0， 则在事件B发生的条件下，事件A发生的条件概率(conditional probability)为：

P(A|B)=P(AB)/P(B)

条件概率是理解全概率公式和贝叶斯公式的基础，可以这样来考虑，如果P(A|B)大于P(A)则表示B的发生使A发生的可能性增大了。

2. 乘法公式

---

 2.1 乘法公式

由条件概率公式得：

 P(AB) = P(B)·P(A|B) = P(A)·P(B|A)

上面的式子就是乘法公式。

2.2 乘法公式的推广

对于任何正整数n≥2，当P(A₁A₂...A_n-1) > 0 时，有：

P(A₁A₂...A_n-1A_n) = P(A₁)P(A₂|A₁)P(A₃|A₁A₂)...P(A_n|A₁A₂...A_n-1)

3. 全概率公式

---

 3.1 前提假设

设B₁，B₂，....为有限或无限个事件，它们两两互斥且在每次试验中至少发生一个，即：

B_i ∩ B_j = ∅（不可能事件）i≠j ,

B₁∪B₂∪.... = Ω（必然事件）.

这时，称事件组 B₁, B₂,...是样本空间Ω的一个划分，把具有这些性质的一组事件称为一个“完备事件组”。

设 B₁, B₂,...是样本空间Ω的一个划分，A为任一事件，则：

 

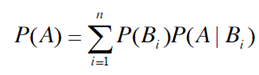
上式即为全概率公式（formula of total probability)

3.2 意义

全概率公式的意义在于，当直接计算P(A)较为困难，而P(B_i)，P(A|B_i)  (i=1,2,...)的计算较为简单时，可以利用全概率公式计算P(A)。思想就是，将事件A分解成几个小事件，通过求小事件的概率，然后相加从而求得事件A的概率，而将事件A进行分割的时候，不是直接对A进行分割，而是先找到样本空间Ω的一个划分B₁,B₂,...B_n,这样事件A就被事件AB₁,AB₂,...AB_n分解成了n部分，即A = AB₁ + AB₂ + ... + AB_n, 每一B_i发生都可能导致A发生相应的概率是P(A|B_i)，由加法公式得

    P(A) = P(AB₁) + P(AB₂) + .... + P(AB_n)

= P(B₁)P(A|B₁) + P(B₂)P(A|B₂) + ... +P(B_n) P(A|B_n)

4. 贝叶斯公式

---

与全概率公式解决的问题相反，贝叶斯公式是建立在条件概率的基础上寻找事件发生的原因（即大事件A已经发生的条件下，分割中的小事件Bi的概率），设B₁,B₂,...是样本空间Ω的一个划分，则对任一事件A（P(A)>0),有

               

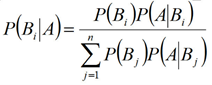
上式即为贝叶斯公式(Bayes formula)，B_i 常被视为导致试验结果A发生的“原因”，P(B_i)(i=1,2,...)表示各种原因发生的可能性大小，故称先验概率（权重）；P(B_i|A)(i=1,2...)则反映当试验产生了结果A之后，再对各种原因概率的新认识，故称后验概率。

5. 小结

---

如果我们把事件A看成“结果”，把诸事件B₁，B₂，…看成是导致这个结果的可能的“原因”，则可以形象地把全概率公式看做“由原因推结果”；而贝叶斯公式则恰好相反，其作用在于“由结果推原因”：现在有一个“结果”A已经发生了，在众多可能的“原因”中，到底是哪一个导致了这个结果？这是一个在日常生活和科学技术中常要问到的问题。贝叶斯公式说，各原因可能性的大小与P(B_i|A)成比例。

贝叶斯公式最神奇之处在于将条件概率中的因和果调换了位置，可以用下面的式子表示：

P(B|A) = P(因|果) = P(因)P(果|因)/P(果)

6. 一个例子

---

问题：

爱丽丝的口袋里有5枚硬币：两枚是正常的硬币（都有正反两面，normal），两枚硬币的两面都是正面（double-headed），最后一枚硬币的两面都是背面（double-tailed）。她随机取出一枚硬币，也没看是哪种硬币，然后投掷：

a). 硬币落地后，朝下的一面为正面的概率？

b). 硬币落地后，正面朝上，那么朝下的一面也是正面的概率？

c). 如果爱丽丝将b)中取到的硬币丢掉，重新从口袋中取出一枚硬币，还是没看是哪种硬币，然后投掷，则当硬币落地后正面朝上的概率？

解答：

设，取出的硬币为normal硬币为事件N;

取出的硬币为double-h硬币为事件H；

取出的硬币为double-t硬币为事件T；

硬币落地后正面朝上为事件A1；

硬币落地后正面朝下为事件A2；

硬币落地后背面朝上为事件B1；

硬币落地后背面朝下为事件B2；

a). 设事件A为硬币落地后朝下的一面为正面，则可分为三种情况，取到normal，取到double-h，取到double-t. 这三种情况可以看作是对取出的硬币的类型这一总样本空间所做的划分。A2也被分成了三种情况，因此可以使用全概率公式，得：

P(A2) = P(A2)*P(N) + P(A2)*P(H) + P(A2)*P(T)

        = 1/2*2/5 + 1*2/5 + 0*1/5

        = 3/5

b). 根据问题和假设，这里要求解的是条件概率P(A2|A1)，也就是在已知正面朝上（A1）这一结果时，求该结果是由取到了double-h这类硬币而导致的概率（由结果推原因）

根据贝叶斯公式可得，P(A2|A1) = P(H|A1) = P(A1H)/P(A1) = P(A1|H)P(H)/P(A1)

P(A1|H)表示在取到double-h时，正面朝上的概率，很明显是1；  

# 此时使用贝叶斯公式的意义就体现出来了，P(H|A1)计算起来并不容易，但经过贝叶斯公式的转换，该条件概率中的因、果发生了交换，交换后的条件概率是非常好计算的

P(H) = 2/5

P(A1) = 3/5  #计算过程同P(A2)

所以，P(A2|A1) = P(A1|H)P(H)/P(A1) = 1 * 2/5 * 3/5 = 2/3

c). 这个问题稍微有点复杂，但也可以分情况讨论：

设该问题——第二次取出的硬币落地后正面朝上，为事件C.

由b)可以知道，b)中取到的硬币只有两种情况(因为事件A1已经发生了)，一种是double-h，令该事件为F；一种是normal，令该事件为G。现在已经知道取double-h的概率P(F) = P(A2|A1) = 2/3，那么P(G) = P(B2|A1) = 1 – P(F) = 1 – 2/3 = 1/3

则P(C) = P(CF) + P(CG)

         = P(F)*P(C|F) + P(G)*P(C|G)  # 全概率公式

         = P(F)*(P(N|F)*1/2 + P(H|F)*1) + P(G)*( P(N|G)*1 + P(H|G)*1)

        # 上式中，橙色部分的概率已经算出来了，绿色部分的式子表示第二次取硬币的情况

        = 2/3 * (2/4 * 1/2 + 1/4 * 1) + 1/3 * (1/4 * 1/2 + 2/4 * 1)

        = 13/24

参考：

http://www.cnblogs.com/ohshit/p/5629581.html

edx上的公开课：MITx: 6.008.1x Computational Probability and Inference

《概率论与数理统计》，陈希孺，中国科学技术大学出版社