结束帝都的qbxt dp图论精讲班后,感觉自己依然很水,接下来的一周,不妨来复习一下讲课内容:)
动态规划是lyd讲的,上次在泉城讲数据结构,然鹅体验较差,这次虽说好了些,但还是比想象中的效果不好(还是我太菜了)。
本篇内容预警:理论知识偏多,warning。
引入:一个沙雕题(IOI1994-数字三角形)
最简单的dp模型,初学者好题。
所以dp到底是啥?可以说,dp是多阶段决策过程的最优化方法。仅就最优化而言,搜索与dp经常干一码事。(dp也常求解方案数)。
在把实际问题划分为dp模型时,我们常用到以下术语。(已经混淆很久)
阶段:每个子问题的求解过程。
状态:(本人经常与阶段弄混)粗糙地说,可以认为是阶段的细化再划分。沙雕题中,就是数塔每层的每一列。
转移:每个最优状态的选取过程
决策:每个最优状态的选取。
而状态转移方程将这几要素有机地进行结合,可以说,思考出转移方程,dp题基本就可拿下。我们思考dp题的目的也就是找出转移方程。
在这里我们作短暂的停留,转移方程常与递推式长的很像。lyd觉得很多人递推和dp傻傻分不清。
我们先给出他的答案:

举个例子
错排问题:这个问题有许多具体的版本,如在写信时将n封信装到n个不同的信封里,有多少种全部装错信封的情况?又比如四人各写一张贺年卡互相赠送,有多少种赠送方法?自己写的贺年卡不能送给自己,所以也是典型的错排问题。
答案:F(n)=(n-1)*(F(n-1)+F(n-2))
怎么得出的呢?参考了一下wikipedia--

所以,lyd又说了--

再进行略微小结(怎么感觉开始大力抄课件..)

例题1 codevs核电站问题
是在序列上的问题,通常我们以下标为状态划分(虽说这是递推)
设f[i]为放到第i个坑位时的方案数。
我们可以分类讨论求解。(没错,oi中许多问题确实可以分类讨论)
显然每个坑位有两种选择:放或是不放。
当i<m,有f[i]=f[i-1]*2
当i==m,有f[i]=f[i-1]*2-1(这里不能再放了,否则会炸)
当i>m,有f[i]=f[i-1]*2-f[i-1-m](减去不能放的方案数)
code

1 #include<cstdio> 2 #include<algorithm> 3 4 using namespace std; 5 typedef long long ll; 6 7 int n,m; 8 ll f[1000]; 9 10 int main() 11 { 12 scanf("%d%d",&n,&m); 13 f[0]=1; 14 for(int i=1;i<=n;i++) 15 { 16 if(i<m) f[i]=f[i-1]*2; 17 else if(i==m) f[i]=f[i-1]*2-1; 18 else if(i>m) f[i]=f[i-1]*2-f[i-1-m];; 19 } 20 printf("%lld",f[n]); 21 return 0; 22 }
例题2 传纸条/方格取数 详见
https://www.cnblogs.com/nopartyfoucaodong/p/9475438.html
例题3 编辑距离 详见
怎么判断一个题是不是dp?(抄lyd课件大全)




两个条件的进一步解读:


Dp与其他算法
一、贪心
二、记忆化搜索
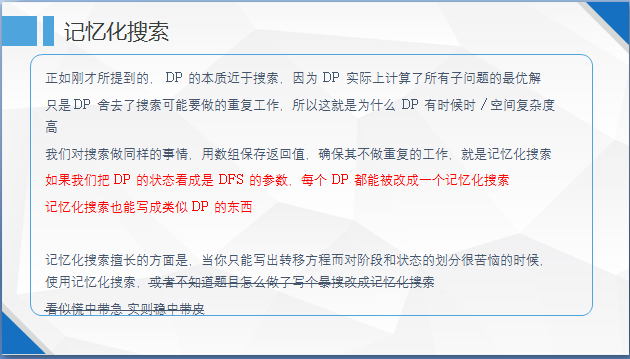

(好吧课件放完了)
聪明的你,是否对dp有了一些新的认识?
附:dalao推荐 TSOI__Vergil
关于dp的认识->绝世好文
