欧拉路径+ST表（模板）

http://poj.org/problem?id=1330

题意：给出一颗树，给出父子关系，求两点的lca。

解法：dfs序+ST表：

原理：

欧拉序（前序遍历得到的序列，叫dfs序，但数字可以重复出现，一进一出，叫欧拉序），会发现根结点总在中间，而根结点是该段序列深度最小的点

因此两个点的LCA，就是在该序列上两个点第一次出现的区间内深度最小的那个点

即在欧拉序中进行ST表在区间中找到最小深度的欧拉序。

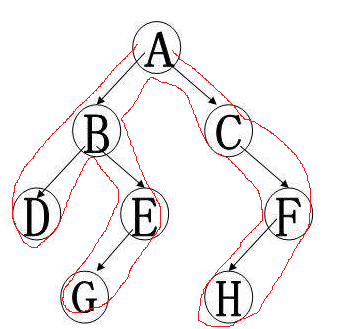
https://www.cnblogs.com/stxy-ferryman/p/7741970.html

 该欧拉序为：ABDBEGEBACFHFCA.

如果要求D、G的lca通过ST表查询D、G间深度最小的欧拉序为B，即为D、G的lca。

从D到G的欧拉路径一定会经过D、G的最近公共祖先，深度最小的结点即为最近公共祖先，转为欧拉序，就是求解区间最小值问题，ST表解决。

见代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 40010, M = 80010;
int pos[N];//记录每个结点的起始欧拉序下标
int oula[M], ti , dep[M];//欧拉序以及欧拉序中的下标对应结点的深度
int dp[M][29];//记录欧拉序区间的深度最小的结点
int e[M] , ne[M] , h[N] , idx ;
int n , q ;
void add(int a , int b){
    e[idx] = b , ne[idx] = h[a] , h[a] = idx++;
}

void dfs(int u, int pre , int d)
{
    oula[++ti] = u;
    dep[ti] = d ;
    pos[u] = ti;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j == pre)
            continue;
        dfs(j, u , d+1);
        oula[++ti] = u;
        dep[ti] = d ;
    }
}

int Min(int x , int y){//返回结点深度小的下标
    return dep[x] < dep[y] ? x : y;
}

void ST()
{
    for (int i = 1; i <= ti; i++)
    {
        dp[i][0] = i ;
    }
    for(int j = 1 ; (1 << j) <= ti ; j++){//枚举区间
        for(int i = 1 ; i + (1 << j) - 1 <= ti ; i++){
            dp[i][j] = Min(dp[i][j-1] , dp[i+(1<<j-1)][j-1]) ;
        }
    }
}
int query(int a , int b){//获取a到b路径上的最小深度的欧拉序下标
    a = pos[a] ;//映射到欧拉序中去
    b = pos[b] ;
    if(a > b) swap(a , b);
    int l = log2(b - a + 1);
    return Min(dp[a][l] , dp[b-(1<<l)+1][l]);
}

int main(){
    #ifdef ONLINE_JUDGE
    #else
        freopen("D:\c++\in.txt", "r", stdin);
        //freopen("D:\c++\out.txt", "w", stdout);
    #endif
    memset(h , -1 , sizeof(h));
    int rt ;
    cin >> n ;
    for(int i = 1 ; i <= n ; i++){
        int a , b ;
        cin >> a >> b ;
        if(b == -1){
            rt = a ;
            continue;
        }
        add(a , b);
        add(b , a);
    }
    dfs(rt , 0 , 1);
    ST();
    cin >> q ;
    while(q--){
        int a , b ;
        cin >> a >> b ;
        cout << oula[query(a , b)] << endl;//返回的是下标转为结点
    }

}