回文子串之Manacher算法

参考和学习的博文：https://blog.csdn.net/ggggiqnypgjg/article/details/6645824?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task

整个算法分为两步：

　　1.对文本字符串做简单的预处理

　　2.线性时间求出辅助数组p 及 答案

第一：

　　在原文本串的每个字符的左边都加上一个特殊字符（例如：‘#’， 字符不会在文本串出现），最后在末尾在加上一个特殊字符

　　例如：

　　　　文本串：abcd

　　　　预处理：#a#b#c#d#

　　之所以这么做是可以把原文本串变成一个长度为奇数的字符串，这样我们就可以根据奇数回文串中心对称的特点来解决

第二：

　　先说明辅助数组 p[ i ] 的含义：即从 i 个 字符 起 往右移动 p [ i ]  下可以移出以 s[ i ] 为 中心的回文串

　　例如：

　

字符串	#	a	#	a	#	b	#	c	#	b	#
下标	1	2	3	4	5	6	7	8	9	10	11
p数组	1	2	3	2	1	2	1	4	1	2	1

　　　　以下标为3的字符 # 为例： 以他为中心的回文串显然是 #a#a# 那么他只需要往右移动三下就可以移出回文串的范围了。

　　接下来讲一下怎么求 p 数组：

　　　　先引入两个变量 mx 和 id；

　　　　mx ： 当前下标的左边的 i + p[ i ] 的 最大值

　　　　id：　mx 对应的下标

　　　　例如 ： 当循环至下标 4 时， mx = 6,  id = 3;　

　　　　计算 p[ i ] 时 可以分两种情况：

　　　　　　一：

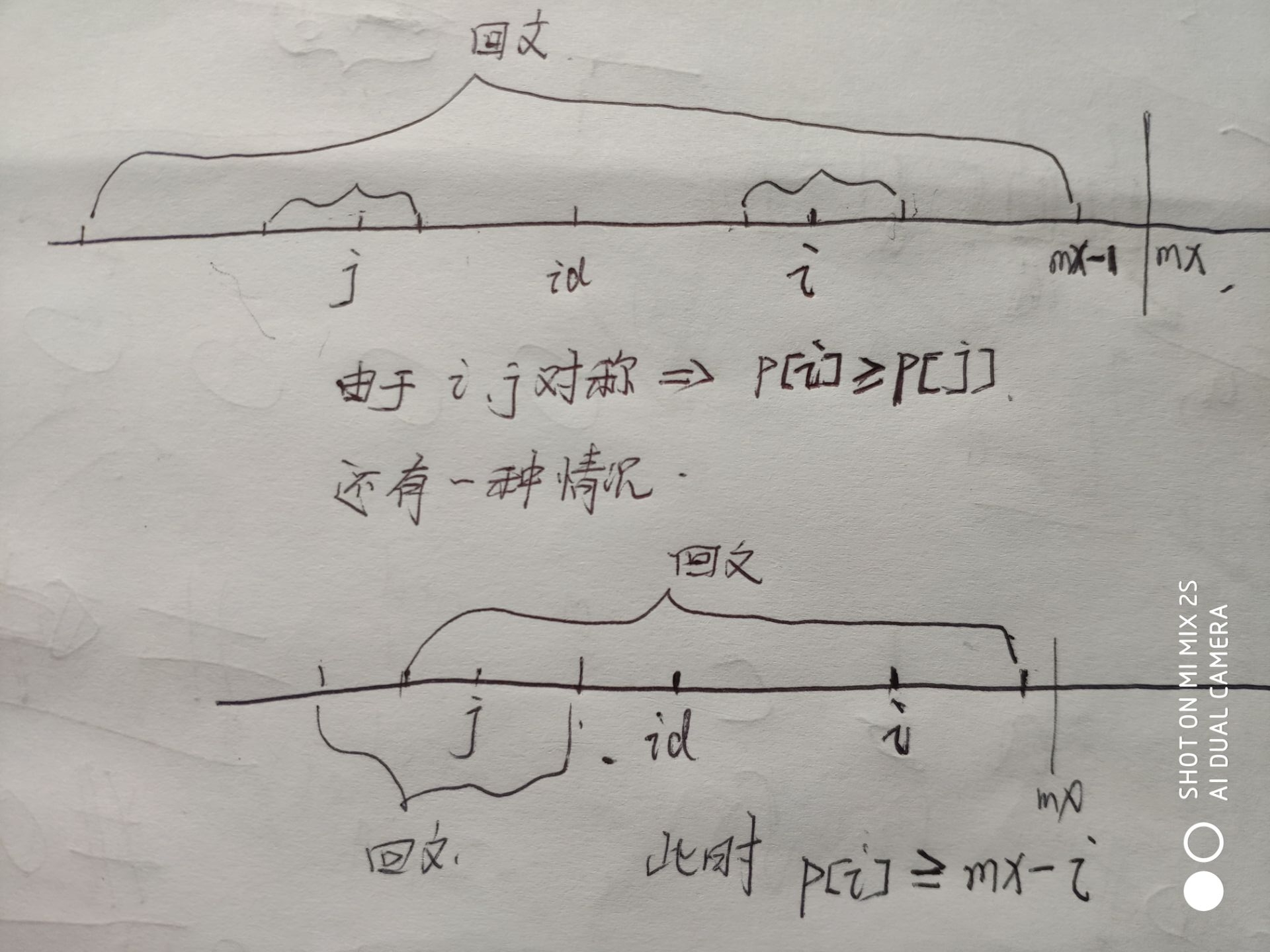
　　　　　　　　mx > i 　　-》  p[ i ] = min( p [ 2 * id - i ] , mx - i )　 　（这是核心）

　　　　　　　　设 j = 2 * id - i； 显然 j  是 i 关于 id 的对称点

　　　　　　　　可以根据这个图片理解上面的式子：

　                     　

　　　　二：赋值 p [ i ] = 1

　　　　接下来在以 i 为 中心， p [ i ] 为 起点循环向左右继续查找； 

　　　　通过观察显然可以发现 原文本串的最长回文串的长度就是 p [ i ] 的最大值 - 1；

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 7;

char s1[N], s2[N * 2];   // s1是原文本串 s2是处理过后的字符串
int p[N * 2];           // 辅助数组

int Manacher(char *s, int len)
{
    int id = 1, mx = 0, res = 0;
    // 字符串是从1到len的
    for(int i = 1; i <= len; i++)
    {
        if(mx > i)   p[i] = min(p[2*id-i], mx-i);
        else            p[i] = 1;
        while(i+p[i] <= len && s[i+p[i]] == s[i-p[i]])
            p[i] ++;
        if(i+p[i] > mx) { mx = i+p[i]; id = i; }
        res = max(res, p[i] - 1);
    }
    return res;
}

int main()
{
    scanf("%s", &s1);
    int lenS1 = strlen(s1);
    int lenS2 = 0;
    // 在每一个字符左右都加上'#'
    for(int i = 0; i < lenS1; i++)
    {
        s2[++lenS2] = '#';  // 下标是从1开始的
        s2[++lenS2] = s1[i];
    }
    s2[++lenS2] = '#';

    cout << Manacher(s2, lenS2) << endl;

    return 0;
}