---恢复内容开始---
红小豆少见的及时更新系列
I three points 1
当大家在枚举少量情况并检验试图找到一个答案的时候,我总是在所有情况里试图构造一个正确的答案
于是大家AK了我也没AC,完。
一个三角形在矩形里放置,并考虑点和边的顺序,有效的情况一共就六种,就算加上“广义三角形”-----直线也是ok的。当固定一个点在原点时,另一个在矩形的边上的点有两种情况,如下图,根据这两点的坐标和此时可知的夹角可以得到第三点的坐标,对其进行边界检查,符合即可输出。因为默认把矩形最长边放在下方,所以根据是否有旋转矩形,还要把点的坐标旋转回去。
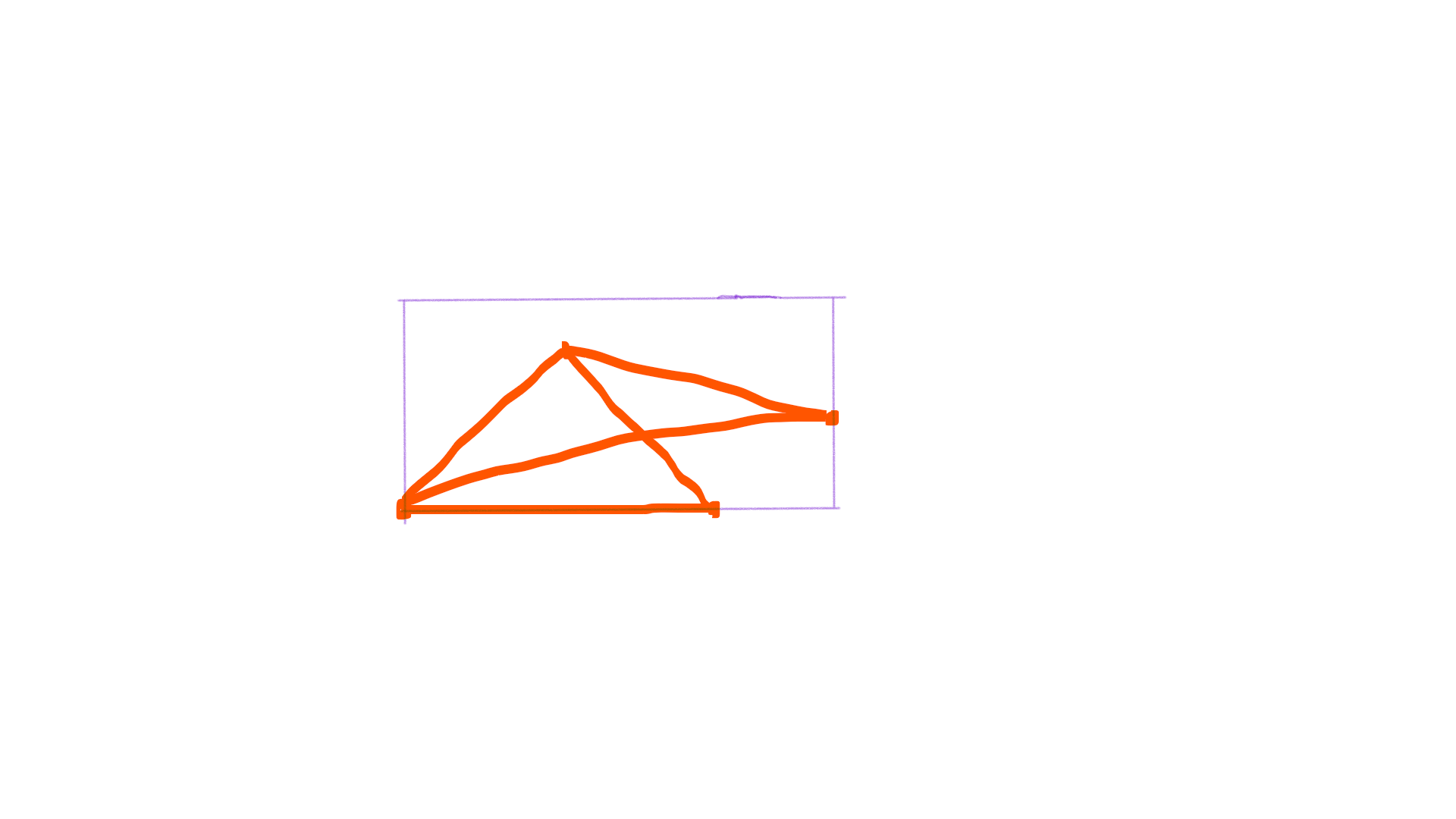
考虑到精度问题没有用acos什么的,所以还要根据情况特判某个角的cos,(场上就各种-nan来着)_(:з」∠)_
场上写的未AC码已经不想看了,重写了一份补题码自我感觉良好

#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<cstring> using namespace std; typedef long long LL; #define CR(t,x) const t&x #define CRP(x) CR(point,x) #define double long double const double eps = 1e-12; double w, h, a[5]; int t; struct point { double x, y; void chg() { swap(x, y); } }p[5]; double dis(CR(point, l), CR(point, r)) { return (l.y - r.y) * (l.y - r.y) + (l.x - r.x) * (l.x - r.x); } int che(int d, int l, int r, int x, int y, int z,bool c) { p[y].y = (a[d] > w) ? (sqrt(a[d] * a[d] - w * w)) : 0; p[y].x = p[y].y ? w : a[d]; double cB = (a[d] * a[d] + a[l] * a[l] - a[r] * a[r]) / (2 * a[d] * a[l]); double sB = sqrt(1 - cB * cB); double cP = p[y].y ? ((a[d] * a[d] + w * w - p[y].y * p[y].y) / (2 * a[d] * w)) : 1; double sP = sqrt(1 - cP * cP); double cQ = cB * cP - sB * sP; double sQ = sqrt(1 - cQ * cQ); p[x].x = p[x].y = 0; p[z].x = a[l] * cQ; p[z].y = a[l] * sQ; if (p[z].x + eps >= 0 && p[z].x - eps <= w && p[z].y + eps >= 0 && p[z].y - eps <= h ) { if (c) { p[x].chg(); p[y].chg(); p[z].chg(); } printf("%.12Lf %.12Lf %.12Lf %.12Lf %.12Lf %.12Lf ", p[1].x, p[1].y, p[2].x, p[2].y, p[3].x, p[3].y); return 1; } return 0; } int main() { scanf("%d", &t); while (t--) { double ma; bool fg = 0; scanf("%Lf%Lf%Lf%Lf%Lf", &w, &h, &a[1], &a[2], &a[3]); ma = max(a[1], max(a[2], a[3])); if (h > w)swap(w, h), fg = 1; if (che(1, 2, 3, 1, 2, 3,fg)); else if (che(1, 3, 2, 2, 1, 3,fg)); else if (che(2, 1, 3, 1, 3, 2,fg)); else if (che(2, 3, 1, 3, 1, 2,fg)); else if (che(3, 2, 1, 3, 2, 1,fg)); else che(3, 1, 2, 2, 3, 1,fg); } return 0; }
---恢复内容结束---
有上面这个东西是因为吃了个饭电脑好像自己重启了_(:з」∠)_
G subsequence 1
应该和020互换题目做的)
这是一道基础dp,出题人如是说。用到了组合数学,补充。
第一维表示s串位置,第二维表示t串位置,存当前方案数:
首先当前方案数以i-1位与j位匹配的方案数为基础;
如果这一位上s比t大,那么 后面n-i位里随便选m-j个的方案数(选了这位之后,后面就可以随便选) 乘上 两个串匹配到上一位的时候的方案数(组合嘛) 就是选择加入这一位提供的答案贡献(直接加进ans里);
如果这一位s和t相等,那么该位的方案数就再加上[i-1][j-1]的时候的方案数,即选ta或者不选ta

#include<iostream> #include<cstdio> #include<algorithm> #include<cmath> #include<cstring> using namespace std; typedef long long LL; const LL mod = 998244353; int t, n, m; char s1[3005], s2[3005]; LL ans; LL c[3005][3005],d[3005][3005]; void C() { c[0][0] = 1; for(int i=1;i<=3000;i++){ c[i][0] = 1; for (int j = 1; j <= 3000; j++) c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod; } } int main() { scanf("%d", &t); C(); while (t--) { scanf("%d%d", &n, &m); scanf("%s %s", s1+1, s2+1); ans = 0; for (int i = 1; i <= n; i++){ if (s1[i] == '0')continue; for (int j = m; j <= n - i; j++) ans = (ans + c[n-i][j]) % mod; } for (int i = 0; i <= n; i++)d[i][0] = 1; for(int i=1;i<=n;i++) for (int j = 1; j <=min(m,i); j++) { d[i][j] = d[i-1][j]; if (s1[i] > s2[j])ans = (ans + d[i-1][j-1] * c[n - i][m - j] % mod) % mod; if (s1[i] == s2[j])d[i][j] = (d[i][j] + d[i - 1][j - 1]) % mod; } cout << ans << endl; } return 0; }
其实[0][0]应该是0的,因为两个空集不会larger than。但是如果第一位就大于的话,就要用到[0][0]来乘组合数,如果ta等于0就会失去一部分方案┓( ´∀` )┏
以上!
