OO第一单元总结
一、度量分析
第一单元的作业我使用预处理模式,预处理模式的业务逻辑很简单从前往后执行即可:
将经过预处理输入的每一行解析为操作数和操作符,并通过操作符和操作数得到结果,并把结果的值存入标签。最后一行标签的值输出即为化简后的表达式
举例:对于一行输入 f5 mul f4 f3 ,操作符为 mul,操作数为标签f4和f3所代表的结果,
通过一次乘法计算得到标签f5所代表的结果并储存后,即可以处理下一行输入。像这样的操作顺序执行n次后,将标签fn所存的表达式输出即为最终表达式。
1.1 类图分析
第一次作业主要实现六种操作符:pos, neg, add, sub, mul, pow 以及直接赋值的操作符null
预处理模式在第一次作业基础上需要进行的增量工作很简单:
- 第二次作业在第一次作业的基础上增加了两类因子
sin因子cos因子和两个操作符sin,cos; - 第三次作业
sin因子和cos因子内部储存的因子自变量除了是x以外,还可以是表达式。
因此程序的主体部分是相同的几乎不需要改动:
Parser类为主要的功能类,由Main类关联控制其生命流程。该类内部属性map:HashMap<Integer,Factor>存有所有标签值和其对应的表达式。
内部方法parseLine处理每行输入的字符串,分配运算器计算操作数的结果并存入map。
Factor接口用来实现储存表达式、因子、项的类;在第一次作业中,项可以通过系数+x指数的方式实现,
在后续作业里由于项内的因子除了x变量因子外还可能包括sin因子 cos因子,因此第二次及以后作业要实现两类因子sinVar和cosVar以及项的类Term ;
StaticTransfer静态类,提供Factor的实现类转化为项或表达式的方法,便于运算器计算。
Operand接口为操作数,操作数可以是标签,可以是变量x,也可以是带符号整数,分别由三个类 Label, VarX, Signum 实现;
接口需要实现getFactor()方法来通过操作数返回一个接口Factor的实现类,其中变量x和带符号整数可以通过此方法直接返回一个变量因子x或者一个带符号整数,
而标签由于需要获取储存的值后代入计算,故Label类的getFactor()方法不实现,取值操作在 Parser类的方法 parseLine内部具体实现;
Binary 和 Unary 接口为双目和单目运算器接口,具体的实现类负责完成操作符代表的运算来处理操作数。
1.1.1 第一次作业的类图:

减法类Sub依赖加法类Add和取反类Neg的实现,幂运算类Pow依赖乘法类Mul的实现;
1.1.2 第二次作业的类图:

第二次作业类图添加了三个Factor接口的实现类:Term,SinVar,CosVar,
他们的实现依赖变量因子类Var的实现,同时添加了两个运算器接口的实现类:Sin,Cos,在第二次作业他们仅需对Factor接口的实现类Var和Numbr处理。
1.1.3 第三次作业的类图:
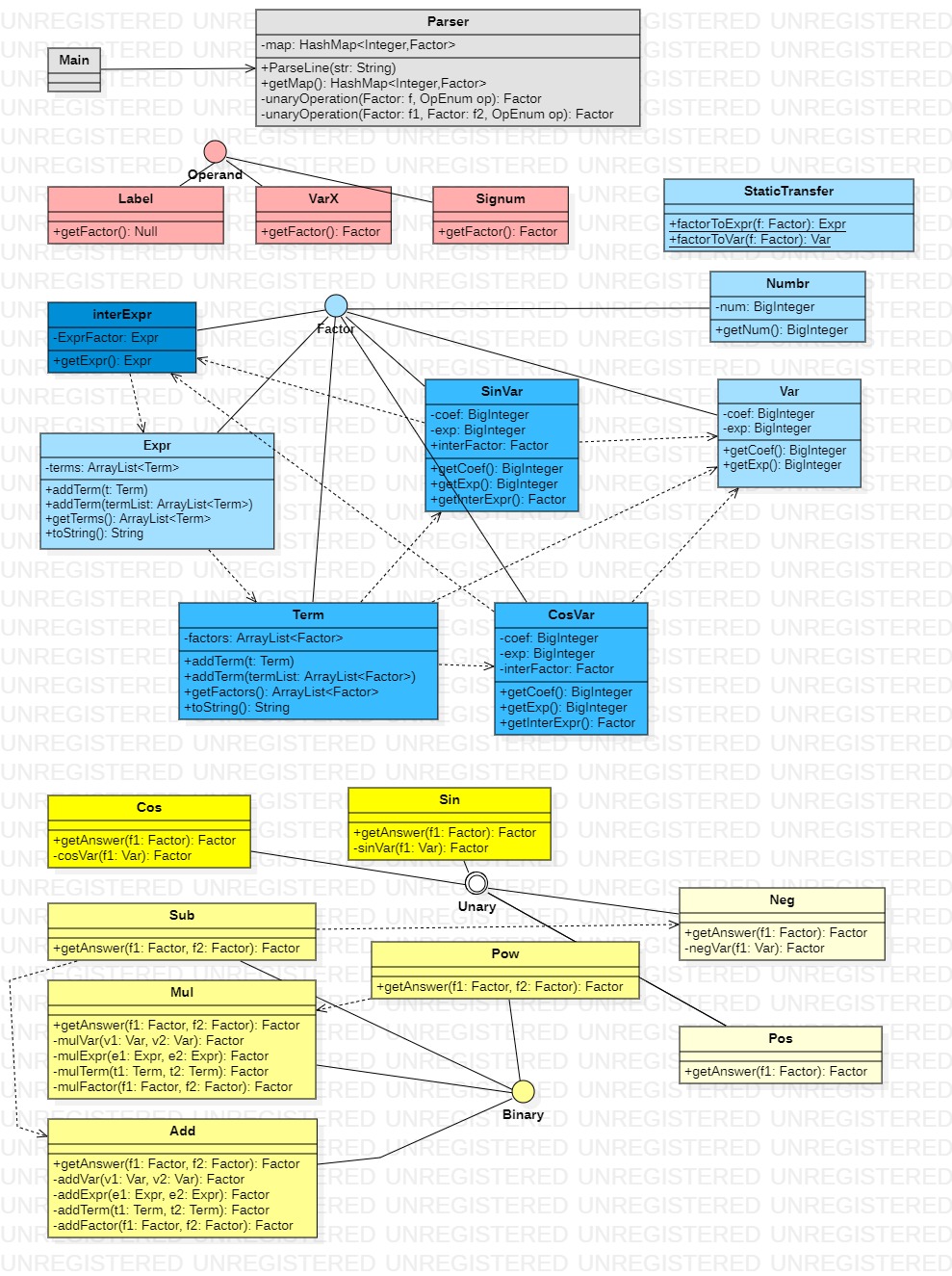
第三次作业类图在第二次基础上添加了内部类因子实现类InterExpr,内部属性有一个类型为Expr的属性ExprFactor,
同时SinVar和CosVar内部储存的属性InterFactor不仅限于变量因子Var,也可能是内部类因子InterExpr,
当其内部储存的属性为内部类因子时,完成了Expr->Term->SinVar/CosVar->InterFactor->Expr的循环依赖;运算器类尤其是Sin和Cos需要相应进行一些修改。
1.1.4 总结:
优点是每个类分工明确单一,减少了耦合,缺点是代码量有点多显得臃肿,类图显得凌乱。
1.2 复杂度度量
以第一次作业为例子,复杂度最高的情况出现在方法Var.toString()上,
这是由于减少输出长度进行情况分类讨论的 if-else分支造成的。整体方法平均圈复杂度在2.3,测试所需分支较少。
@Override
public String toString() {
if (coef.equals(BigInteger.ZERO)) {
return "0";
} else {
if (exp.equals(BigInteger.ZERO)) {
return this.coef.toString();
} else {
if (coef.equals(BigInteger.ONE)) {
if (exp.equals(BigInteger.ONE)) {
return "x";
} else {
return "x**" + exp.toString();
}
} else if (coef.equals(BigInteger.ONE.negate())) {
if (exp.equals(BigInteger.ONE)) {
return "-x";
} else {
return "-x**" + exp.toString();
}
} else {
if (exp.equals(BigInteger.ONE)) {
return coef.toString() + "*x";
} else {
return coef.toString() + "*x**" + exp.toString();
}
}
}
}
}
| method | ev(G) | iv(G) | v(G) |
|---|---|---|---|
| expr.Var.toString() | 8.0 | 8.0 | 8.0 |
| calculator.Add.addFactor(Factor,Factor) | 3.0 | 3.0 | 4.0 |
| calculator.Mul.mulFactor(Factor,Factor) | 3.0 | 3.0 | 4.0 |
| calculator.Neg.getAnswer(Factor) | 3.0 | 4.0 | 4.0 |
| calculator.Pow.getAnswer(Factor,Factor) | 3.0 | 3.0 | 3.0 |
| calculator.Pow.powInt(Factor,BigInteger) | 3.0 | 4.0 | 4.0 |
| calculator.Add.addVar(Var,Var) | 2.0 | 2.0 | 2.0 |
| calculator.Add.getAnswer(Factor,Factor) | 2.0 | 2.0 | 4.0 |
| calculator.Mul.getAnswer(Factor,Factor) | 2.0 | 2.0 | 4.0 |
| option.Operator.Operator(String) | 2.0 | 2.0 | 8.0 |
| Main.main(String[]) | 1.0 | 3.0 | 3.0 |
| Parser.Parser() | 1.0 | 1.0 | 1.0 |
| Parser.binaryOperation(Factor,Factor,OpEnum) | 1.0 | 7.0 | 7.0 |
| Parser.getMap() | 1.0 | 1.0 | 1.0 |
| Parser.parseLine(String) | 1.0 | 3.0 | 5.0 |
| Parser.strToFactor(String) | 1.0 | 3.0 | 3.0 |
| Parser.unaryOperation(Factor,OpEnum) | 1.0 | 3.0 | 3.0 |
| calculator.Add.addExpr(Expr,Expr) | 1.0 | 1.0 | 1.0 |
| calculator.Mul.mulExpr(Expr,Expr) | 1.0 | 3.0 | 3.0 |
| calculator.Mul.mulVar(Var,Var) | 1.0 | 1.0 | 1.0 |
| calculator.Neg.negVar(Var) | 1.0 | 1.0 | 1.0 |
| calculator.Pos.getAnswer(Factor) | 1.0 | 1.0 | 1.0 |
| calculator.StaticTransfer.factorToExpr(Factor) | 1.0 | 3.0 | 5.0 |
| calculator.StaticTransfer.factorToVar(Factor) | 1.0 | 2.0 | 3.0 |
| calculator.Sub.getAnswer(Factor,Factor) | 1.0 | 1.0 | 1.0 |
| expr.Expr.Expr() | 1.0 | 1.0 | 1.0 |
| expr.Expr.Expr(ArrayList) | 1.0 | 1.0 | 1.0 |
| expr.Expr.addTerm(ArrayList) | 1.0 | 1.0 | 1.0 |
| expr.Expr.addTerm(Var) | 1.0 | 1.0 | 1.0 |
| expr.Expr.getTerms() | 1.0 | 1.0 | 1.0 |
| expr.Expr.toString() | 1.0 | 4.0 | 4.0 |
| expr.Numbr.Numbr(BigInteger) | 1.0 | 1.0 | 1.0 |
| expr.Numbr.getNum() | 1.0 | 1.0 | 1.0 |
| expr.Numbr.toString() | 1.0 | 1.0 | 1.0 |
| expr.Var.Var() | 1.0 | 1.0 | 1.0 |
| expr.Var.Var(BigInteger,BigInteger) | 1.0 | 1.0 | 1.0 |
| expr.Var.getCoef() | 1.0 | 1.0 | 1.0 |
| expr.Var.getExp() | 1.0 | 1.0 | 1.0 |
| option.Label.Label(String) | 1.0 | 1.0 | 1.0 |
| option.Label.Label(int) | 1.0 | 1.0 | 1.0 |
| option.Label.getFactor() | 1.0 | 1.0 | 1.0 |
| option.Label.getKey() | 1.0 | 1.0 | 1.0 |
| option.Operator.getOp() | 1.0 | 1.0 | 1.0 |
| option.SigNum.SigNum(BigInteger) | 1.0 | 1.0 | 1.0 |
| option.SigNum.SigNum(String) | 1.0 | 1.0 | 1.0 |
| option.SigNum.getFactor() | 1.0 | 1.0 | 1.0 |
| option.VarX.getFactor() | 1.0 | 1.0 | 1.0 |
| Total | 68.0 | 92.0 | 109.0 |
| Average | 1.446808510638298 | 1.9574468085106382 | 2.3191489361702127 |
后续两次作业圈复杂度较高的情况也出现在toString方法的分类讨论和运算器类需要处理多个Factor接口实现类的分类讨论中,就不一一分析。
二、Bug分析
2.1 自身bug分析
第二次公测所出现的bug:用int来储存带符号整数,导致输入时对超大整数处理的异常,以及超大整数运算超过了int范围后结果错误;
第三次互测被hack数0;
我个人通常在编写代码debug的时候,习惯完成一个类的编写后通过idea的Alt+Enter快捷键对其方法构造JUnit单元测试。
例如测试Mul类的方法getAnswer(Factor f1, Factor f2)的具体单元测试类似如下:
尽可能覆盖该方法所有的模块分支,观察其行为是否符合设计预期。
class XxxTest { // xxx classname
Xxx x;
@BeforeEach
void setUp() {
ArrayList<parameterType> list1 = new ArrayList<>();
ArrayList<parameterType> list2 = new ArrayList<>();
parameterType item11 = ...;
parameterType item12 = ...;
...
parameterType item21 = ...;
parameterType item22 = ...;
...
list1.add(item11);
list1.add(item12);
...
list2.add(item21);
list2.add(item22);
...
}
@Test
void xx() { // xx methodname
int cnt = 0;
for (parameterType i : List1){
for (parameterType j : List2){
System.out.println("cnt: " + cnt + " | " + i.toString() + " " + j.toString());
cnt++;
parameterType k = Xxx.xx(i, j);// ans
System.out.println("ansTypeis: " + k.getClass().getTypeName() + " | " + k.toString());
}
}
}
}
在所有类的单元测试之后会编写一些简单的测试用例进行集成测试。
这样的好处是不需要额外的时间成本编写自动化测试或者对拍,只要最终的代码符合设计预期就结束测试,
如果有已知的测试用例未能通过能很快定位bug位置;
这样的坏处是如果设计阶段没能考虑的情况,例如一些边界情况则有可能测试不到。无法解决意料之外的bug。
2.2互测发现别人bug
结合被测程序的代码设计结构来设计测试用例对我来说有点难,看懂别人代码需要花很长时间。
我采取的测试策略通常为将他人的代码视为一个黑箱,直接用自己的测试用例来测他人代码。这个策略几乎不具有什么有效性,我hack不到什么人。
三、架构设计体验
预处理模式的业务逻辑很直接,所以迭代工作量很少,从无到有考虑架构的开始是最困难的,
不过开始编写代码后,一边想一边写,写着写着就知道自己需要什么了。
另外idea的Refactor功能很强大,把重复的代码提取成方法,把专一职能包装成类,能有效减少模块复杂度和减少类之间的耦合。
四、心得体会
研讨课的讨论给我的印象很深,大家都觉得简化表达式真的很难,讨论的时候几乎全部在谈各自的简化方法,
有些方法很有启发性感觉给我打开了一扇窗,真的能在结构上简化表达式,有些方法则感觉像是先射箭再画靶,不具有通用性。