hdu1024 Max Sum Plus Plus

Max Sum Plus Plus

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 40437    Accepted Submission(s): 14558

Problem Description

Now I think you have got an AC in Ignatius.L's "Max Sum" problem. To be a brave ACMer, we always challenge ourselves to more difficult problems. Now you are faced with a more difficult problem.

Given a consecutive number sequence S₁, S₂, S₃, S₄ ... S_x, ... S_n (1 ≤ x ≤ n ≤ 1,000,000, -32768 ≤ S_x ≤ 32767). We define a function sum(i, j) = S_i + ... + S_j (1 ≤ i ≤ j ≤ n).

Now given an integer m (m > 0), your task is to find m pairs of i and j which make sum(i₁, j₁) + sum(i₂, j₂) + sum(i₃, j₃) + ... + sum(i_m, j_m) maximal (i_x ≤ i_y ≤ j_x or i_x ≤ j_y ≤ j_x is not allowed).

But I`m lazy, I don't want to write a special-judge module, so you don't have to output m pairs of i and j, just output the maximal summation of sum(i_x, j_x)(1 ≤ x ≤ m) instead. ^_^

 

 

Input

Each test case will begin with two integers m and n, followed by n integers S₁, S₂, S₃ ... S_n.
Process to the end of file.

 

 

Output

Output the maximal summation described above in one line.

 

 

Sample Input

1 3 1 2 3

2 6 -1 4 -2 3 -2 3

 

 

Sample Output

6 8

Hint

Huge input, scanf and dynamic programming is recommended.

题目链接：

http://acm.hdu.edu.cn/showproblem.php?pid=1024

题目大意：

一个长度为n的序列，求出最大m个子段的序列元素和

思路：

这题的数据特别大，用暴力显然是不行的，所以得想别的方法。

我们可以先看暴力做法的大致思路：首先，我们应该是遍历每一种将n个数选取m段连续子段然后求出他们的最大和，再从这些数里找出前m段相加就是答案，从这个思路中我们可以得到要求出答案，就要先将n个数中选取m段。

因此，我们可以将问题拆分成若干个子问题，求出子问题的最优解，然后在子问题的最优解中挑选出最优解，即得到答案。

现在，我们将问题拆分。

先从1段开始分析：n个数选取1段的最大的和是多少。我们从第一个数开始选，这时的问题就是选一个数作为一段，显然就是这个数的值，然后我们再看第二个数，这时我们就要考虑这两种情况（1：不选这个数和更大。2：选这个数和更大（这种情况不能仅仅用之前选出的最大值+这个数，看第三个数你就知道了）），我们从这两种情况中得出最大的值就是从两个数中选取1段的最优解，我们再看第三个数，也要考虑要不要选他，我们用一个例子来说明：

假设，我们是1，-2，3这三个数，我们在第一第二步得出的最大和都是1（在第二个数时，我们不选取-2，所以最大值仍是1），当到第三个数时，我们因去遍历前面的每一个与3有关的连续字段得出最大值（显然这个值是只选第三个），而不是用前面2个数求出的值+3了（那样的话值为4，显然是错误的）。这时我们得出了3，他和前面1相比取大就好了。

后面的以此类推，一直到第n个数，我们就把n个数分成1段对于每个数的所有最优解求出来了，接下来我们看分成2段时的求法。

选取两段：两段时，我们应该从第二个数开始，因为大于等于两个数才能分成两段，第二个数时的最大和也就是他们俩的和，那我们再看第三个数时，我们也是考虑要不要把它加到分两段的情况里，那我们也有那两种情况（选与不选），选的话我们就要从头遍历前面分成2段时与这个数有关的所有情况，显然这时不行的，那我们应该怎么做呢？我们将选取两段分成先选取一段，求出一段的最优解，再在分两段时从这个数前面分一段的最优解中选取最大值加上这个数和不选这个数取最大就行了。

 

选取n段：同上面一样，我们就可以从n-1段中得到答案。

 

看一下样例2的过程：

可以看到最后答案为8。

 

接下来看状态转移方程：dp[i][j]=max(dp[i][j-1],max(dp[i-1][k]+a[j]))  (i<=k<j)

 

现在问题来了，如果这样解决问题的话，时空复杂度都是很高的。

 

所以要进行优化：

 

在时间上，我们可以把最大值不断存下来，减去遍历更新的时间消耗；在空间上，可以发现每次更新当前数的最大值时，只需要用到上一次（即比这一次少一段的dp值）和当前数字，所以我们可以使用滚动数组来减少空间的消耗。

 

代码如下：

 

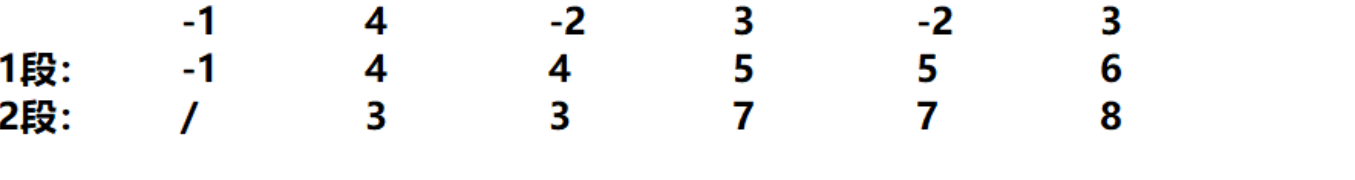
#include<stdio.h>
#include<iostream>
#include<string.h>
using namespace std;

long long dp[2][1001000],num[1001000]; //滚动数组dp，前缀和num->为了减少当子段数很大时遍历前缀求和所花费时间 
long long maxx;
int main()
{
    long long n,m,k;
    while(scanf("%lld%lld",&n,&m)!=EOF)
    {
        int t=0;
        memset(dp,0,sizeof(dp));
        memset(num,0,sizeof(num));
        maxx=0;
        for(int i=1;i<=m;i++)
        {
            scanf("%lld",&k);
            num[i]=num[i-1]+k;
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=i;j<=m;j++)
            {
                if(i==j) maxx=dp[t][j]=num[j];  //当i==j时 当前最大值为前j项和，即dp数组为num[j] 
                else
                {
                    maxx=max(maxx,dp[1-t][j-1])+num[j]-num[j-1];   //maxx更新 
                    dp[t][j]=max(dp[t][j-1],maxx);
                }
            }
            t=1-t;   //数组滚动 
        }
        t=1-t;   //滚动数组最后一次遍历后 与 答案数组相反 进行一次t的改变 
        cout<<dp[t][m]<<endl;
    }
    return 0; 
}