1 众所周知时间序列属于一种数据集合。这类数据集合尤其独到的特点。正如我们需要分析其他数据一样,时间序列这类数据也需要很多模型去解释和预测它。但是所适用分析的模型都是建立在某某假设的基础上的,换言之只要某某假设条件完全符合,其对应的模型就会基本上是“完美”的。但是显示中分析的对象(时间序列数据)并不能很好的使用这种假设,因此建模之前我们需要进行数据清洗的工作。
2 数据清洗是比较形象的比喻,其核心的思想是把时间序列的数据进行抽丝剥茧,就像洋葱一样,如果每层拆分的好,其整个过程的结果就是去符合这种模型的分析对象。这里面的思想前提是:时间序列好像围绕着我们身边看不见摸不着的无线电波信息,每一个时间序列的节点和这些节点串联起来的实际序列数据其背后或者说内在是包含在各种各样的信息在里面。这也就是说明了,在一个复杂的信息集合是很难用一个合理的模型去解释的。在Fama的市场有效性假说中提到的“弱有效市场”层面,对应的阿尔法都是时不时的显现,其“发出的声音”都是比较微弱的。我们只有把这些信息一层一层的从整个时间序列数据的这个大的集合抽离出来,抽离的越“纯”,其表示某一方面的信息越纯粹,如果某一方面的信息越纯粹了,其可对应相关模型的分析效果越明显。所以总结如下:
(1) 数据清洗是任何模型分析之前的首要工作。
(2) 数据清洗的好与坏的标准在于每抽离一层信息,所能表示的“本征”越纯粹越好。
(3) 把所有抽离出来的信息组合到一起就会还原成原有的时间序列的模样,这是一个可逆的过程。
3 在打个比喻,物质呈现各种各样的性质,其原子内的特征都是大差不差的。我们首要做的工作就是找到你所需要而想要分析的那一层本来的特征表示。这就是工作所在。
4 因此时间序列和信号分析的呈现特征尤其非常相似的特点。我们抽离时间序列的一些本征信息的时候会用到很多信号分析的手段。
5 EMD经验模态分解算法(Empirical Mode Decomposition,一般指的是EMD算法)是HHT(Hilbert-Huang)变化的核心算法。由美国NASA的黄鄂博士提出的一种信息分析方法。他一句数据自身的持久尺度特征阿里进行信号分解,无须预先设定任何基函数(这不像是小波分析或者傅里叶变换之类)
它是适合于Fenix非线性、非平稳信息序列具有很高的信噪比。
6 EMD经验模态分解算法的基本简介之希尔伯特---黄变换:
信号处理一直是许多科学研究和应用领域的关键步骤,而自然界中的信号(时间序列数据也是一种信号)几乎都是各种信号的叠加,这里既有平稳的线性信号(如果时间序列都是线性的了就不用分析了),基本上都是大量的非线性非平稳的信号(时间序列的诸多模型的前提条件就是要求数据的平稳性,所以信号处理的这种分析思路很使用对于数据的分析)。传统的基于傅里叶变换的信号处理技术在处理信号时,把信号从整个时域变换到频域,用信号所包含的全部频率成分来描述信号在频域内的变化,不能够反应出局部信号频率的瞬时变化,这在处理非线性信号时具有难以避免的局限性。并且传统的方法受到测不准原理的限制,不能同时在时间和频率上同时达到很高的精度。
后来,人们提出的加窗傅里叶变换在某种程度上克服了傅里叶变换的缺点,实现了分析信号的局部性质,但它仍然存在一些不足。
首先,一旦选定窗口大小,如果信号在时间或频率上的变化区域小于窗口的话,窗口内信号平稳的假设就不能成立,这时再用加窗傅里叶变换分析非平稳信号时,信号的局部特征就难以反映。
其次,加窗傅里叶变换在时频面上依然要满足测不准原理,而窗函数一旦选定,就不能任意调整,所以加窗傅里叶变换不能在时间和频率两方面同时达到很高的分辨率。
目前应用非常广泛的小波变换虽然在处理非线性非平稳信号的能力上有了进一步提高,但其本质还是一种可调的傅里叶变换,不可避免的具有窗函数的局限性,仍受测不准原理限制,无法精确描述频率随时间的变化,且小波变换存在着众多的小波基函数,而各小波从基函数的使用范围很不一致,这就造成了小波基的选择问题。
这也是一致困扰着小波变换研究和应用者的问题;另一个问题就是不具有良好的自适应新,一旦小波被选定后,必须用他来分析所有的数据。
1998年,美国华裔科学家黄鄂提出了一种新型非线性非稳态的信号处理方法-------希尔伯特-黄变换HHT。HHT方法从信号自身的特征出发,用经验模态分解EMD方法把信号分解成一系列的本征模态函数,然后对这些IMF(也就是本质模态)分量进行希尔伯特变换,从而得到时频平面上能量分布的Hilbert谱图,打破了测不准原理的限制,可以精确的表达信号在时频面上面的各类信息。其中就有可能获得你所需要分析时间序列数据序列中的趋势信息、噪声信息、周期信息和季节信息。
7 HHT方法的基本定义:
传统的信号分析与处理都是建立在傅里叶分析的基础上的,他有3个基本假设:线性、高斯性和平稳性,建立的是一种理想的模型。但是不能分析局部性能。因此不适用于非线性非平稳的信号。
8 EMD分解方法:
假设:
(1) 信号最少有一个极大值和一个极小值
(2) 时域特性由极值间隔决定
(3) 如果数据序列完全缺乏极值但是仅包含拐点,那么它也可以通过一次或多次求导来表示极值点,而最终结果可以由这些成分求积分获得。
IMF(Intrinsic Mode Function)本征模函数:
Intrinsic:本征,固有的,内在的,本质的。
Huang等人认为任何信号都是由若干本征模函数组成的,任何时候一个信号都可以包含若干个本征模函数,如果本征模函数之间相互重叠,便形成符合信号。EMD分解的目的就是为了获取本征函数。
3种测量时间尺度的方法:
1.相邻两过零点间隔的时间尺度。
2.相邻两极值点间隔的尺度。
3.相邻两曲率极值点间隔的时间尺度。
IMF分量必须满足下面两个条件:
1.其极值点个数和过零点数相同或最多相差一个。
2.其上下包络关于时间轴局部对称。
IMF函数必须满足的两个条件:
1.函数在整个时间范围内,局部极值点和过零点的数据必须相等,或最多相差一个。
2.在任意时刻点,局部最大值的包络(上包络线)和局部最小值的包络线(下包络线)平均必须为0。
分解过程:
1.找出原数据序列X(t)所有的极大值点并用三次样条插值函数拟合形成原数据的上包络线;同样,找出所有的最小值点,并将所有的极小值点通过三次样条插值函数拟合现成数据的下包络线,上包络线和下包络线的均值记做m1,将原数据序列X(t)减去该平均包络m1,得到一个新的数据序列h1:
X(t) - m1 = h1;
由原数据减去包络平均后的新数据,若还存在负的局部极大值和正的局部极小值,说明这还不是一个本征模函数,还要继续进行筛选。
EMD分解过程停止准则:
1.当最优一个基本模式分量或剩余分量,变得比预期值小时变停止;
2.当剩余分量变成单调函数,从而从中不能再筛选出基本模式分量为止。
实际准则:
上下过程的停止准则可以通过限制两个连续的处理结果之间的标准差的大小来实现,通常取0.2-0.3
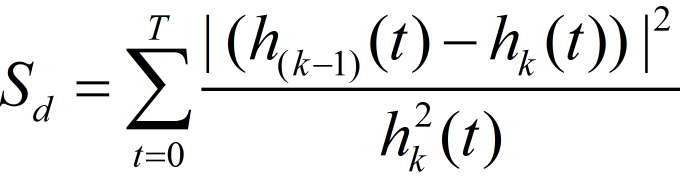
表征整体正交性的指标IO(Index of Orthogonal)定义为:
