1 第一个问题:最大似然估计是什么?从分类上来说属于概率论中的点估计方式。
2 由Fisher这个人才在1912年重新提出,最早提出还是数学王子高斯。不过准确的说他属于数理统计的范畴。
3 概率论和数理统计是互逆的思想过程。概率论可以看成是由因推果,数理统计则是由果溯因。互为逆思考的过程。
4 正如我们提到的数学,不在于眼花缭乱的公式提炼,首先应该每一个细节的意义,这个是最终要的。是精华部分。
5 似然估计(有的教材叫拟然估计)。就看英文名likelihood estimate(LE),而likelihood的意思是可能性。知道一个现象,他可能是由什么因引起的。概念性的解释一下:在传统概率学派中假定的是概率分布的参数固定,随机样本。那么我们该如何谈过样本去确定这个概率分布的参数呢?这里就需要用到似然估计的方法了。也就是说,样本出现后,反推模型参数值,而这个参数值有多种可能性(M,最Max,最大的可能性。最大似然估计也叫Max likelihood estimate MLE)。
举个例子,假设我们有很多块西瓜皮,瓜皮的纹路分为清洗、稍微模糊、模糊,现在我们的目的就是通过瓜皮去推断西瓜的成熟程度(瓜青,瓜烂,瓜熟)。
但是现实生活中,我们的关注点一般都只希望得到最好的参数(也就是希望当前瓜皮所对应的西瓜最大可能成熟程度),也就是说,我们只希望得到那个使得样本发生可能性最大的参数,其余低可能性的我们不考虑。所以通俗来说,最大似然 ======>>>最有可能的情况。
6 案例1:加入有一个管子,里面有黑白两种颜色的球,数目多少不知道,两种颜色比例也不知道,我们想知道罐中白球和黑球的比例,但我们不能把罐子中的球全部拿出来数(球太多了,耽误我玩儿dota)。现在我们可以每次任意从已经均摇一摇的罐子中拿出一个球来,记录求的颜色,然后把拿出来的球再放回罐子中。这个过程可以重复,我们用以记录球的颜色来估计罐子中的黑白球的比例。加入我们前面的一百次重复记录中,有60次是白去,请问罐子的白球所占的比率最优可能是多少?
答案:70%,如果你的答案和上面一样,恭喜你,你已经用了最大似然估计了。
解:
我们用随机X来表示所抽取球的颜色,则X=1表示白球;X=0表示黑球,那么X服从伯努利分布b(1,p),(伯努利分布也叫二项分布,非黑即白的分布形式)其中p是箱子中白球的比例,抽出100个球得样本x1,x2,x3....,xn,这批观测值的概率表示为如下:
L(p),叫做时间的联合概率(我们知道之前说的概率的条件叫独立事件,如果连续性发生的时间,连续性,也叫连续数据,不同于离散型的数据)
L(p) = P (X1 = x1, ... , X100 = x100 ; p)
= P(x1;p) * p(x2;p) * ... * p(x100;p)
=p70(1-p)30
根据最大似然的思想,我们应该选择p使得上面的公式值是最大的,讲上式对p求导,并零这个导函数为0,(这里解释一样,为什么使得导函数为0,求导的过程就是求极限的斜率,是属于极限的思想,如果这个极限趋近于0,肯定是有一个值为0了)。
求导:∂L(p)/∂p = 70/p-30/1-p=0 , p=70/100=0.7
(注:这里求导用到了一个复合函数的求导过程:三部曲:分层(从外向内分解成基本函数用到中间变量);层层求导;做积分还原。常用的积分求导如下:
y = 5 dy = 0
y=x4 dy= 4x3
y=x-2 dy = -2x-3=-2/x3
y=2x dy = 2xln2
7 这里是伯努利分布,也就是0和1的情况,如果情况不知一种,如果情况如果是4种呢?
3,1,3,0,3,1,2,3
(1)最大似然函数的累乘形式。
3的情况出现4次,因此(1-2p)4
1的情况出现2次,因此(2p(1-p)2
0出现的情况1次,因此p2
2出现的情况1次,因此p2
(2) 把这些累乘起来
L(p) = (1-2p)4(2p(1-p))2p2p2
(3) 整理一下
4p6(1-p)2(1-2p)4
(4) 比较方便的性质求复合函数求导,可以取对数形式。
ln4 + 6lnp +2ln(1-p)+4ln(1-2p)
(5) 求导
6/p - 2/1-p-8/(1-2p) = 0,求出p
8 这里用了似然函数的通项式
还是7的题目,
X ~ (0 1 2 3)
p2 2p(1-p) p2 1-2p
上面的平方就是出现的次数。专业点儿的说叫分布律。
9 相关知识的再总结:
(1) 极大似然估计的思想基础:平时人们思维过程中养成的习惯,比如一个得到过奥运金牌打把脱靶性的可能性(概率)大大小于没有打过枪的人的脱靶性。发生可能性大的发生的结果就是事实。这是平时人们思考问题的基础。
(2) 极大似然估计的原理:
如果X~f(x),f(x)为整个样本X的密度函数。
如果我们做了N次试验,x1,x2,...,xn对应的密度函数就是f(x1),f(x2),...,f(xn)。
我们就认为:这些所有的密度函数累乘就是最大值。也是做试验最可能发生的结果。这个最大值也叫极大。
问题:为什么是累乘(连乘)。因为这里不是求每一次概率密度函数的最大值,而是求每一次联合起来的最大值,联合起来就是相乘,然后他们的最大值是乘完之后的最大值,而不是每一个的最大值。如果是每一个的最大是连加。这里要注意。
(3) 有了上面(2)所说的原理我们就可以写成一个最大似然估计联合分布律的通式(注意这里是联合,要用累乘符号大π):
πp(xi;θ),其中π : i = 1...n
(4) 又有了上面(3)的联合分布律的表示,我们就可以把极大似然估计的函数写出了,叫似然函数(有了这个函数我们就可以在知道结果的情况下,取估计参数)。
设:x1,x2,...,xn是相应于样本X1,X2,...,Xn的一个样本值,因此这些概率事件可以写成{X1 = x1, X2 = x2,...,Xn = xn},我们就可以知道这个概率值θ如何用似然函数写出了:
L(θ) = L(x1,x2,...,xn ;θ) = πp(xi;θ),θ∈Θ,其中π:i = 1..n,其中这一概率随θ的取值而变化,它是θ的函数,其中x1,x2...都是已知的样本值,都是常数。
实验结果已经固定了,反过来θ取哪一个值最靠谱?也就是θ使得这个L这个值最大的那个值最靠谱。
(5) 举例:如果X~b(1,p).X1,X2,...,Xn是来自X的一个样本,试求参数p的最大似然估计量。
解:这是一个二项分布。又因为这是个离散型的数据,因此要把每一个点的概率求出来,然后再相乘就是似然估计的p,另外要求极值,我们就要乘积,乘积的求导挺麻烦的,乘积的求导也叫复合函数求导。这里求导不方便,我们就把它对数化就可以把幂拿下来,而且就可做加法了。比如:
L = p(X1 = x1)*p(X2 = x2)*...*p(Xn = Xn)
lnL = lnp(X1 = x1) + lnp(X2 = x2)+...+lnp(Xn = Xn)
我们把它对数化之后,因为对数函数是单调的,所以求p的最大值也就是求lnL的最大值。这里的Xi的概率只有两种,如果Xi = 0的话 p等于1-p,如果Xi = 1的话 p等于p。因为这是二项分布,不是0就是1。
因此一般分两步:第一步是写出似然函数,第二步求导得最大值(最大值也就是等于0)。
截图如下:
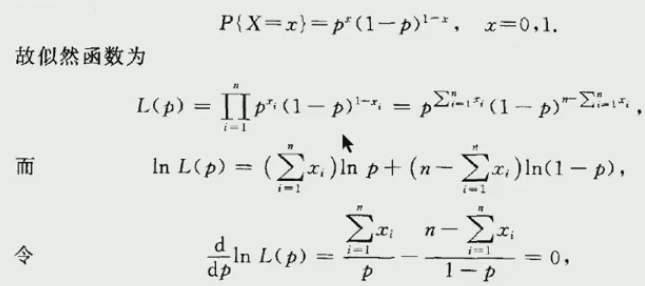
(6) 举例:我们在举一个连续型的函数,未知数为两个μ和sigma平方,这里不是求导数,是求偏导的过程,因为这里是偏导。截图如下: