1. 联合概率
由多个随机变量决定的概率我们就叫联合概率,它的概率分布就是联合概率分布。随机变量 x 和 y 的联合概率使用 P(x, y) 表示
那么联合概率和单个随机变量的概率之间有什么关联呢?对于离散型随机变量,我们可以通过通过联合概率 P(x, y) 在 y 上求和,就可以得到 P(x)。对于连续型随机变量,我们可以通过联合概率 P(x, y) 在 y 上的积分,推导出概率 P(x)。这个时候,我们称 P(x) 为边缘概率。
除了边缘概率的推导,多个变量的联合概率和单个变量的概率之间还存在一个有趣的关系。在解释这个关系之前,让先来介绍条件概率。
条件概率也是由多个随机变量决定,但是和联合概率不同的是,它计算了给定某个(或多个)随机变量的情况下,另一个(或多个)随机变量出现的概率,其概率分布叫做条件概率分布。给定随机变量 x,随机变量 y 的条件概率使用 P(y | x) 表示。
解释清楚了条件概率,我就可以列出概率、条件概率和联合概率之间的“三角”关系了。简单的说,联合概率是条件概率和概率的乘积,采用通用的公式来表达就是:


概率、条件概率和联合概率之间的这种“三角”关系,也是著名的贝叶斯定理的核心,下面来详细解释什么是贝叶斯定理,以及它可以运用在什么场景之中。
2. 贝叶斯定理
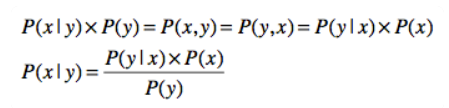
(1)在这里面,我们把 P(x) 称为先验概率。之所以称为“先验”,是因为它是从数据资料统计得到的,不需要经过贝叶斯定理的推算。
(2)P(y | x) 是给定 x 之后 y 出现的条件概率。在统计学中,我们也把 P(y | x) 写作似然函数 L(y | x)。在数学里,似然函数和概率是有区别的。概率是指已经知道模型的参数来预测结果,而似然函数是根据观测到的结果数据,来预估模型的参数。不过,当 y 值给定的时候,两者在数值上是相等的,在应用中我们可以不用细究。
(3)另外,我们没有必要事先知道 P(y)。P(y) 可以通过联合概率 P(x, y) 计算边缘概率得来,而联合概率 P(x, y) 可以由 P(y|x) * P(x) 推出。针对离散型和连续型的边缘概率推导分别如下:

而 P(x|y) 是根据贝叶斯定理,通过先验概率 P(x)、似然函数 P(y | x) 和边缘概率 P(y) 推算而来,因此我们把它称作后验概率。
3. 随机变量之间的独立性
相互独立会产生一些有趣的现象
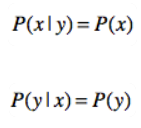
另外,将 p(x | y) = p(x) 带入贝叶斯公式,就可以得出:
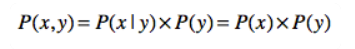
变量之间的独立性,可以帮我们简化计算。举个例子,假设有 6 个随机变量,而每个变量有 10 种可能的取值,那么计算它们的联合概率 p(x1, x2, x3, x4, x5, x6),在实际中是非常困难的一件事情。
根据排列,可能的联合取值,会达到 10 的 6 次方,也就是 100 万这么多。那么使用实际的数据进行统计时,我们也至少需要这个数量级的样本,否则的话很多联合概率分布的值就是 0,产生了数据稀疏的问题。但是,如果假设这些随机变量都是相互独立的,那么我们就可以将联合概率 p(x1, x2, x3, x4, x5, x6) 转换为 p(x1) * p(x2) * p(x3) * p(x4) * p(x5) * p(x6)。如此一来,我们只需要计算 p(x1) 到 p(x6 ) 就行了。
在实际项目中,我们会假设多个随机变量是相互独立的,并基于这个假设大幅简化计算,降低对数据统计量的要求。虽然这个假设通常是不成立的,但是仍然可以帮助我们得到近似的解。相比较实现的可行性和求解的精确度,可行性更为重要。在讲解朴素贝叶斯方法中,充分利用这一点,从有限的训练样本中构建分类器。
思考题
大年三十晚上,爷爷奶奶发红包。爷爷准备的红包是 4 个 50 元的,6 个 100 元的。奶奶准备的红包是 8 个 50 元的,4 个 100 元的。全家人随机抽,你运气很好,拿到一个 100 元的红包。请问这个红包来自爷爷的概率有多少?来自奶奶的概率有多少?
①设事件x:抽中100元红包;
事件y:抽到爷爷的红包。
则100元的红包来自爷爷的概率:P(y|x) = P (x,y) / P(x) = (6/22) / (10/22) = 0.6
100元红包来自奶奶的概率为:0.4
②随机变量 X 的取值:爷爷、奶奶,随机变量 Y 的取值:50 、100。
问题:求解 P(X=爷爷|Y=100) 、P(X=奶奶|Y=100) 。
由统计数据可知:
P(Y=100) = (6 + 4) / (4 + 6 + 8 + 4) = 5/11
P(X=爷爷, Y=100) = 6 / (4 + 6 + 8 + 4) = 3/11
P(X=奶奶, Y=100) = 4 / (4 + 6 + 8 + 4) = 2/11
则:
P(X=爷爷|Y=100) = P(X=爷爷, Y=100) / P(Y=100) = 3/5
P(X=奶奶|Y=100) = P(X=奶奶, Y=100) / P(Y=100) = 2/5