一、AOV网络与拓扑排序
AOV网(Activity On Vertex NetWork)用顶点表示活动,边表示活动(顶点)发生的先后关系。
若网中所有活动均可以排出先后顺序(任两个活动之间均确定先后顺序),则称网是拓扑有序的。
1、算法步骤
- 在网络中选择一个入度为0的顶点输出;
- 在图中删除该顶点及所有以该顶点为起点的边;
- 重复上述过程,直至所有边均被输出。
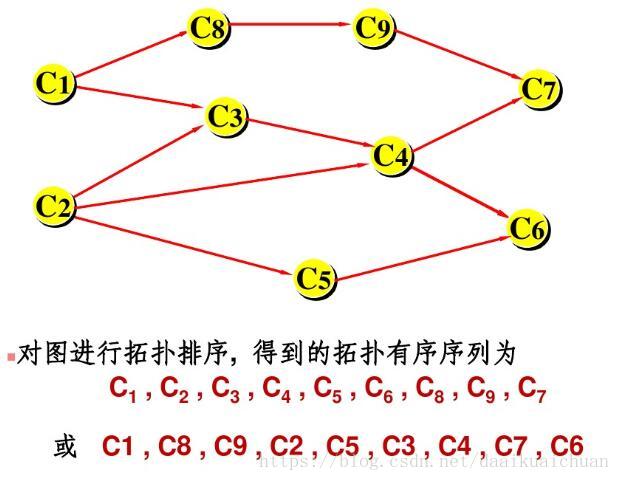
2、算法图解
3、算法demo:
#include <bits/stdc++.h>
using namespace std;
const int M = 10001;
int matrix[M][M];
int indegree[M]; //book已排序的顶点个数
int main(int argc, char const *argv[])
{
int i, j, a, b, k, book = 0, n, m;
cin >> n >> m;
for (i = 1; i <= m; ++i)
{
cin >> a >> b;
matrix[a][b]=1;
indegree[b]++;
}
for (i = 1; i <= n; ++i)
{
for (j = 1; j <= n; ++j)
{
if (indegree[j] == 0)
{
cout << j << " ";
//遍历所有入度为0的顶点
indegree[j] = -1;
book++;
for (k=1; k <= n; k++)
{
if (matrix[j][k] == 1)
{
//遍历所有入度为1的顶点
matrix[j][k] = 0;
indegree[k]--;
}
}
break;
}
}
}
system("pause");
return 0;
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
二、AOE网络
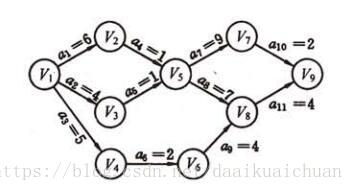
AOE网的定义:在带权有向图中若以顶点表示事件,有向边表示活动,边上的权值表示该活动持续的时间,这样的图简称为AOE网。
如上所示,共有11项活动(11条边),9个事件(9个顶点)。整个工程只有一个开始点和一个完成点。即只有一个入度为零的点(源点)和只有一个出度为零的点(汇点)。
关键路径:是从开始点到完成点的最长路径的长度。路径的长度是边上活动耗费的时间。如上图所示,1 到2 到 5到7到9是关键路径(关键路径不止一条,请输出字典序最小的),权值的和为18。
三、AOV网络与AOE网络的关系
从定义上来看,很容易看出两种网的不同,AOV网的活动以顶点表示,而AOE网的活动以有向边来表示,AOV网的有向边仅仅表示活动的先后次序。纵观这两种网图,其实它们总体网络结构是一样的,仅仅是活动所表示的方式不同,因此可以猜想从AOV网转换成AOE网应该是可行的。
通常AOE网都是和关键路径联系在一起的,在AOE网中我们可以通过关键路径法来计算影响整个工期的关键路径,达到缩短工期的目的。在传统的AOV网中是没有表示活动时间的权值的,因此传统的AOV网无法估算工期,但是如果我们在AOV网中的活动结点上都标上时间属性,那么AOV网就可以完全转换为AOE网。