1、冒泡排序原理
-
直观点先看图(注:图片来源于网络)
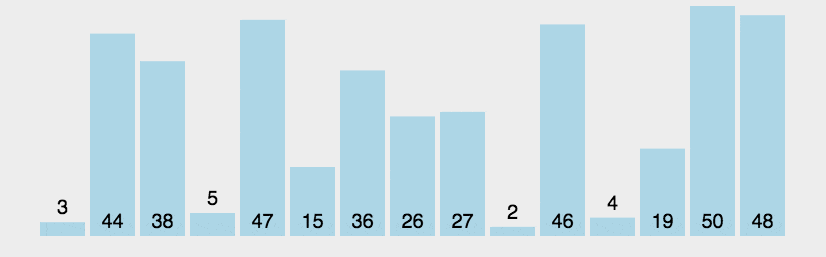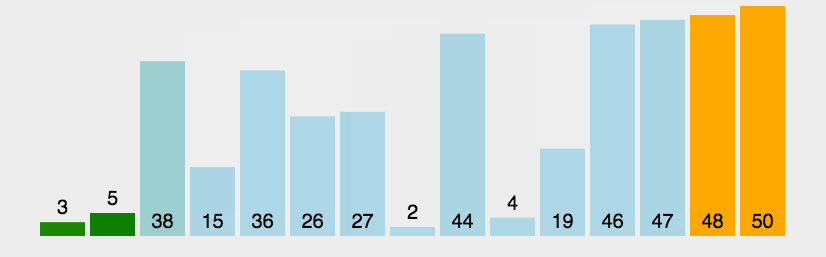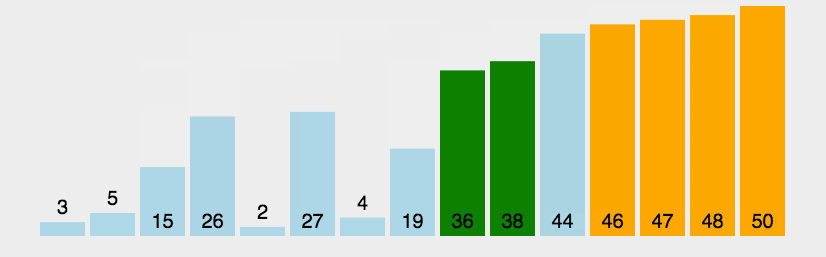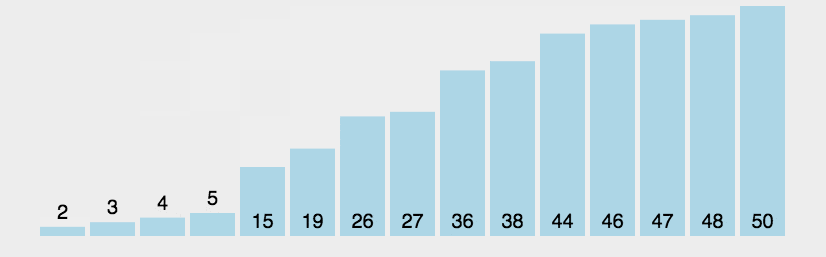
从上图我们可以看出冒泡排序的规则,归纳几点如下:
冒泡的规则:
-
每一轮获取第一个数和后面的数据进行依次比较的过程,称为一轮冒泡的过程
-
每一轮冒泡.都是先拿第一个数,依次比对相邻的两个数,如果前一个数比后一个数大,则交换他们的位置,这一轮比较完毕,会把最大的数放在最后面。
-
然后反复重复上面的步骤(每一轮都能将前面数据中一个最大数,放到后面),直到一轮冒泡下来没有任何数据需交互位置,此时数据已经为有序状态
冒泡的次数:
假设列表的长度为n,冒泡排序是每次拿出来第一个元素,需要拿多少次呢?应该是列表的长度减1,意味着每一个长度为n的列表,需要冒泡 n-1 次
每次冒泡比较的次数:
每一次冒泡,都能排好一个数据的顺序,第一次冒泡,需要进行依次比较的次数为n次,那么随着次的增加排好的数据也会越多,需要比较的数据就越少。关系图如下:
| 第几次冒泡 | 比较的次数 |
|---|---|
| 1 | n-1 |
| 2 | n-2 |
| 3 | n-3 |
| 4 | n-4 |
根据以上分析我们找出了冒泡次数和,比较次数的关系,接下来就可以通过代码来实现了,实现代码如下:
2、python实现冒泡排序
代码实现:
li = [22, 3, 44, 112, 1, 442, 55, 33, 65] def bubble_sort(li): n = len(li) # 遍历列表长度减1次 for i in range(1, n): # 每次遍历都获取第一个元素,依次和后面的元素进行比较 for j in range(n - i): # 判断前元素,和后一个元素的值 if li[j] > li[j + 1]: # 交换当前元素和后一个元素的值 li[j], li[j + 1] = li[j + 1], li[j] return li
注意:上面的代码根据冒泡的思路,实现了排序,但是从严格意义上讲还是由缺陷的,不能算是真正的冒泡排序,只是一个伪冒泡排序,面试能够把这个伪冒泡排序写出来,大多数公司还是能过的。
3、代码优化
众所周知,进行冒泡排序的时候,按正常的逻辑来讲,当一轮冒泡下来,所有数据的顺序都没发生改变,那么该数据就是一个有序列表了,这个时候就不会在进行下一轮冒泡了,
例如:当我们使用一个有序列表来进行冒泡排序,那么第一轮冒泡下来,所有的数据顺序都不会发生改变,那么就不会再进行下一轮冒泡,这样情况下时间复杂度为最优,只进行一轮冒泡,即O(n)。
1、缺陷分析
针对于时间复杂度最优的这种情况,在上面写的伪冒泡排序算法中是不可能出现的,不管被排序的数据有没有顺序,都会进行n-1次冒泡,即最坏时间复杂度。
在这边上面的伪冒泡只考虑了冒泡的过程,不管列表原来的顺序,依次冒泡,全部去排一遍顺序,没有从时间复杂度的角度去做优化。
2、代码优化
针对上述缺陷问题,接下来我们进行优化
代码如下:
def bubble_sort(li): n = len(li) # 遍历列表长度减1次 for i in range(1, n): # 创建一个变量,用来记录本轮冒泡,是否有数据交换位置 status = False # 每次遍历都获取第一个元素,依次和后面的元素进行比较 for j in range(n - i): # 判断前元素,和后一个元素的值 if li[j] > li[j + 1]: # 交换当前元素和后一个元素的值 li[j], li[j + 1] = li[j + 1], li[j] # 只要由数据交换位置,则修改statusd的值 status = True # 每一轮冒泡结束之后,判断当前status是否为Flase, # 如果为Flase,则说明上一轮冒泡没有修改任何数据的顺序(即数据是有序的) if not status: return li return li
代码解释:上述代码对之前的伪冒泡进行了优化,主要优化的点在于,我们每一次冒泡的时候,设置一个变量来记录,当前这次冒泡数据的顺序是否有发生改变,初始值设为False,当数据属性发生改变时,就把这个值设为True,一轮冒泡结束后 再去判断,这个变量是否为False,如果为False则没有发生改变,即数据有序,那么接下来就可以直接返回数据,不需要再进行下一次冒泡。
提示:看完文章的小伙伴,以后面试遇到冒泡排序的时候不要再写伪冒泡了!