| 朋友圈转发信息 | |
| 描述: |
在一个社交应用中,两个用户设定朋友关系后,则可以互相收到对方发布或转发的信息。当一个用户发布或转发一条信息时,他的所有朋友都能收到该信息。 现给定一组用户,及用户之间的朋友关系。 问:当某用户发布一条信息之后,为了让每个人都能在最早时间收到这条信息,这条信息最少需要被转发几次? 假设:对所有用户而言: 1)朋友发出信息到自己收到该信息的时延为T(T>0); 2)如需转发,从收到信息到转发出信息的时延为0。 用例保证:在给定的朋友圈关系中,任何人发布的信息总是能通过N(N>=0)次转发让其他所有用户收到。 例如: 下图表示某个朋友圈关系(节点间连线表示朋友关系)中,用户1在时刻0发布信息之后,两种不同的转发策略。 黄色节点表示转发用户,蓝色数字为用户收到信息的时间。 |
| 运行时间限制: | 无限制 |
| 内存限制: | 无限制 |
| 输入: |
Sender [消息创建者编号] Relationship [朋友关系列表,1,2 表示1和2是朋友关系] End 如下: Sender |
| 输出: |
当某用户发布一条信息之后,为了让每个人都能在最早时间收到这条信息,这条信息最少需要被转发的次数 |
| 样例输入: |
Sender 1 Relationship 1,2 1,3 1,4 2,5 2,6 3,6 4,6 4,7 5,6 5,8 5,9 6,7 6,8 6,9 7,9 10,7 End |
| 样例输出: |
4 |
| 答案提示: | |
题意:
一棵树,当某用户发布一条信息之后,为了让每个人都能在最早时间收到这条信息,这条信息最少需要被转发的次数。
题解:
可以发现,每个用户接受到信息的时间,是他到起点(消息创建者编号)消息创建着的最短路,故先用最短路预处理。
然后可以发现,收到消息时间为 T 的用户是否选择发布消息,只会影响到 2T的用户,(因为,时间T的用户的儿子一定是时间为2T的用户,因为每个人都要最早收到消息),而影响不到3T、4T......的用户。 类似的,2T用户的决策影响3T用户。
那么,问题就简化成选最少的上层用户,让下层每个用户都收到最早消息,也就是一个二分图问题。
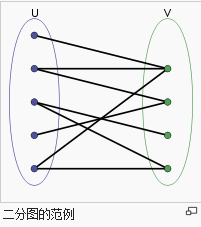
即 从u到v,要求能到达v的每一点,u中需要的最小点数。
对于这个匹配问题,窝是没想出什么太好的方法,网上传的一个贪心的做法是错误的。
由于不知道数据范围,开始没敢暴力,不过,经kss测试,数据范围很小,可以暴力,那么把上层集合状压暴力一下就好。
一个剪枝:如果下层某个用户只有一个上层的父亲节点,那么该父亲节点必选。
| 1643144 | 陈志阳 | Q5J7H45T | 朋友圈转发信息 | 正确 | C++ | 3H 24M 40S | 160 | 2015-03-26 21:01:07 |
1 #include <cstdio> 2 #include <cstring> 3 #include <stack> 4 #include <vector> 5 #include <queue> 6 #include <algorithm> 7 8 #define ll long long 9 int const N = 105; 10 int const M = 205; 11 int const inf = 1000000000; 12 ll const mod = 1000000007; 13 14 using namespace std; 15 16 int root; 17 vector<int> ibian[N]; 18 vector<int> dbian[N]; 19 vector<int> ubian[N]; 20 int ru[N]; 21 int chu[N]; 22 char s[N]; 23 int ans; 24 vector<int> b[N]; 25 int d[N]; 26 typedef pair<int,int> P; 27 int vis[N]; 28 int totcen; 29 30 void ini() 31 { 32 int i; 33 ans=0; 34 memset(ru,0,sizeof(ru)); 35 memset(chu,0,sizeof(chu)); 36 memset(vis,0,sizeof(vis)); 37 for(i=0;i<=100;i++){ 38 ibian[i].clear(); 39 ubian[i].clear(); 40 dbian[i].clear(); 41 b[i].clear(); 42 d[i]=inf; 43 } 44 totcen=0; 45 } 46 47 void dijkstr() 48 { 49 priority_queue<P,vector<P>,greater<P> > que; 50 d[root]=0; 51 que.push(P(0,root)); 52 vector<int>::iterator it; 53 while(que.size()>=1) 54 { 55 P p=que.top();que.pop(); 56 int v=p.second; 57 if(d[v]<p.first) continue; 58 for(it=ibian[v].begin();it!=ibian[v].end();it++){ 59 int index=*it; 60 if(d[index]>d[v]+1){ 61 d[index]=d[v]+1; 62 que.push(P(d[index],index)); 63 } 64 } 65 } 66 } 67 68 void ini2() 69 { 70 vector<int>::iterator it1; 71 vector<int>::iterator it2; 72 for(int i=0;i<=100;i++){ 73 if(d[i]==inf) continue; 74 totcen=max(totcen,d[i]); 75 b[ d[i] ].push_back(i); 76 } 77 for(int i=0;i<=totcen;i++){ 78 for(it1=b[i].begin();it1!=b[i].end();it1++){ 79 int u=*it1; 80 for(it2=ibian[u].begin();it2!=ibian[u].end();it2++){ 81 int v=*it2; 82 //printf(" u=%d v=%d du=%d dv=%d ",u,v,d[u],d[v]); 83 if( d[v]!=d[u]+1 ) continue; 84 dbian[u].push_back(v); 85 ubian[v].push_back(u); 86 chu[u]++; 87 ru[v]++; 88 } 89 } 90 } 91 92 /* 93 for(int i=0;i<=100;i++){ 94 if(b[i].size()==0) continue; 95 printf(" i=%d ",i); 96 for(it1=b[i].begin();it1!=b[i].end();it1++){ 97 int y=*it1; 98 printf(" %d ru=%d chu=%d ",y,ru[y],chu[y]); 99 } 100 printf(" "); 101 }*/ 102 } 103 104 void cal(int up,int down) 105 { 106 memset(vis,0,sizeof(vis)); 107 vector<int>::iterator it1; 108 vector<int>::iterator it2; 109 int u,v,vv; 110 int te=inf; 111 int cntu,cntd; 112 cntu=cntd=0; 113 //int tot; 114 int now; 115 int uu[N]; 116 // int dd[N]; 117 //tot=b[down].size(); 118 for(it2=b[down].begin();it2!=b[down].end();it2++) 119 { 120 v=*it2; 121 //printf(" v=%d ",v); 122 if(vis[v]==1) continue; 123 if(ru[v]==1){ 124 vis[v]=1; 125 u=*ubian[v].begin(); 126 //printf(" u=%d ",u); 127 vis[u]=1; 128 ans++; 129 for(it1=dbian[u].begin();it1!=dbian[u].end();it1++){ 130 vv=*it1; 131 vis[vv]=1; 132 } 133 } 134 } 135 136 for(it1=b[up].begin();it1!=b[up].end();it1++){ 137 u=*it1; 138 if(vis[u]==1) continue; 139 uu[cntu]=u; 140 cntu++; 141 } 142 143 for(it2=b[down].begin();it2!=b[down].end();it2++){ 144 v=*it2; 145 if(vis[v]==1) continue; 146 // dd[cntd]=v; 147 cntd++; 148 } 149 if(cntd==0) return; 150 int o,j; 151 int vis2[N]; 152 int cou; 153 for(o=0;o<(1<<cntu);o++) 154 { 155 //printf(" o=%d ",o); 156 memset(vis2,0,sizeof(vis2)); 157 now=0; 158 cou=0; 159 for(j=0;j<cntu;j++){ 160 if( (1<<j) & o ){ 161 u=uu[j]; 162 cou++; 163 for(it1=dbian[u].begin();it1!=dbian[u].end();it1++){ 164 v=*it1; 165 if(vis[v]==1) continue; 166 if(vis2[v]==0){ 167 now++;vis2[v]=1; 168 } 169 } 170 } 171 } 172 if(now==cntd){ 173 te=min(te,cou); 174 } 175 } 176 ans+=te; 177 } 178 179 void fun() 180 { 181 int i; 182 for(i=1;i<totcen;i++){ 183 cal(i,i+1); 184 } 185 } 186 187 void solve() 188 { 189 //printf(" aftdi "); 190 dijkstr(); 191 //printf(" inidi "); 192 ini2(); 193 //printf(" fundi "); 194 fun(); 195 } 196 197 void out() 198 { 199 printf("%d ",ans); 200 } 201 202 int main() 203 { 204 int u,v; 205 //freopen("data.in","r",stdin); 206 //scanf("%d",&T); 207 // for(cnt=1;cnt<=T;cnt++) 208 //while(T--) 209 ini(); 210 scanf("%s",s); 211 scanf("%d",&root); 212 scanf("%s",s); 213 while(scanf("%s",s)!=EOF) 214 { 215 if(s[0]=='E') break; 216 sscanf(s,"%d,%d",&u,&v); 217 ibian[u].push_back(v); 218 ibian[v].push_back(u); 219 } 220 solve(); 221 out(); 222 }
