leetcode 42 接雨水 左右逢源

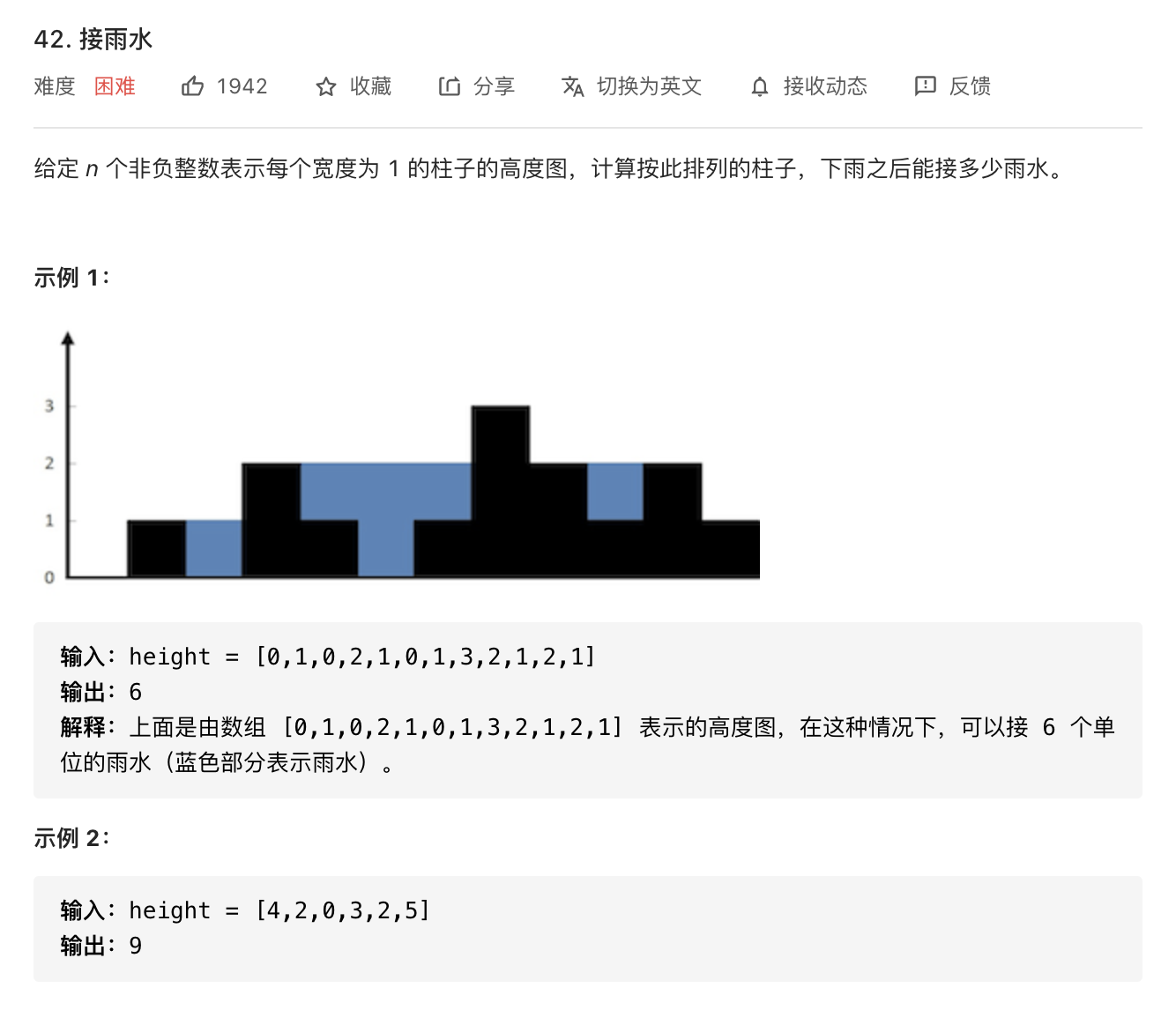
　　JAVA 暴力解法，这一步是比较难的，该思路我称之为左右逢源。视角放在局部，每个元素对应的结果与左右所有元素相关：

    public final int trap(int[] height) {
        int re = 0, len = height.length;
        for (int i = 1; i < len - 1; i++) {
            int maxLeft = 0, maxRight = 0;
            for (int j = i; j >= 0; j--) maxLeft = Math.max(height[j], maxLeft);
            for (int j = i; j < len; j++) maxRight = Math.max(height[j], maxRight);
            re += Math.min(maxLeft, maxRight) - height[i];
        }
        return re;
    }

　　暴力解法有思路后，很容易看出计算过程中的重复计算部分，进行缓存：

    public final int trap(int[] height) {
        int re = 0, len = height.length;
        int[][] cache = new int[len][2];
        for (int i = 1; i < len - 1; i++) {
            int maxLeft = 0, maxRight = 0;
            if (cache[i - 1][0] > 0) maxLeft = Math.max(cache[i - 1][0], height[i]);
            else for (int j = i; j >= 0; j--) maxLeft = Math.max(height[j], maxLeft);
            if (cache[i + 1][1] > 0) maxRight = Math.max(cache[i + 1][1], height[i]);
            else for (int j = i; j < len; j++) maxRight = Math.max(height[j], maxRight);
            cache[i] = new int[]{maxLeft, maxRight};
            re += Math.min(maxLeft, maxRight) - height[i];
        }
        return re;
    }

　　随着计算过程发现，左侧缓存被充分利用起来了，但右边并没有进行缓存。

　　在计算过程中顺便缓存，注定只能缓存一边。索性将缓存的建立拿到计算过程外面，提前缓存，计算时查表：

    public final int trap(int[] height) {
        int re = 0, len = height.length;
        if (len == 0) return 0;
        int[] maxLefts = new int[len], maxRights = new int[len];
        maxLefts[0] = height[0];
        maxRights[len - 1] = height[len - 1];
        for (int i = 1; i < len; i++) maxLefts[i] = Math.max(maxLefts[i - 1], height[i]);
        for (int i = len - 2; i >= 0; i--) maxRights[i] = Math.max(maxRights[i + 1], height[i]);
        for (int i = 1; i < len - 1; i++) re += Math.min(maxLefts[i], maxRights[i]) - height[i];
        return re;
    }

　　JS：

/**
 * @param {number[]} height
 * @return {number}
 */
var trap = function (height) {
    if (!height || height.length == 0) return 0;
    let re = 0, len = height.length, maxLefts = new Array(len), maxRights = new Array(len), last = len - 1;
    maxLefts[0] = height[0];
    maxRights[last] = height[last];
    for (let i = 1; i < len; i++) maxLefts[i] = Math.max(maxLefts[i - 1], height[i]);
    for (let i = last - 1; i >= 0; i--) maxRights[i] = Math.max(maxRights[i + 1], height[i]);
    for (let i = 1; i < last; i++) re += Math.min(maxLefts[i], maxRights[i]) - height[i];
    return re;
};