Leetcode 11 盛水最多的容器 贪心算法

 

　　暴力解法很容易：

    /**
     * @Author Niuxy
     * @Date 2020/7/9 9:49 下午
     * @Description 暴力解法
     */
    public final int maxArea0(int[] height) {
        int max = 0;
        for (int i = 0; i < height.length; i++) {
            for (int j = i + 1; j < height.length; j++) {
                int length = Math.min(height[j], height[i]);
                length = length < 0 ? length * -1 : length;
                max = Math.max(max, (j - i) * length);
            }
        }
        return max;
    }

　　时间复杂度为 O(n²)。

　　想办法优化，想要从重复计算入手，结果发现整个计算过程并没有什么重复计算。

　　因为容量是由较短的一边乘以两边的长度得出的，而不是一个一个小格子累加起来的。

　　重复计算走不通，想办法去避免无效计算。

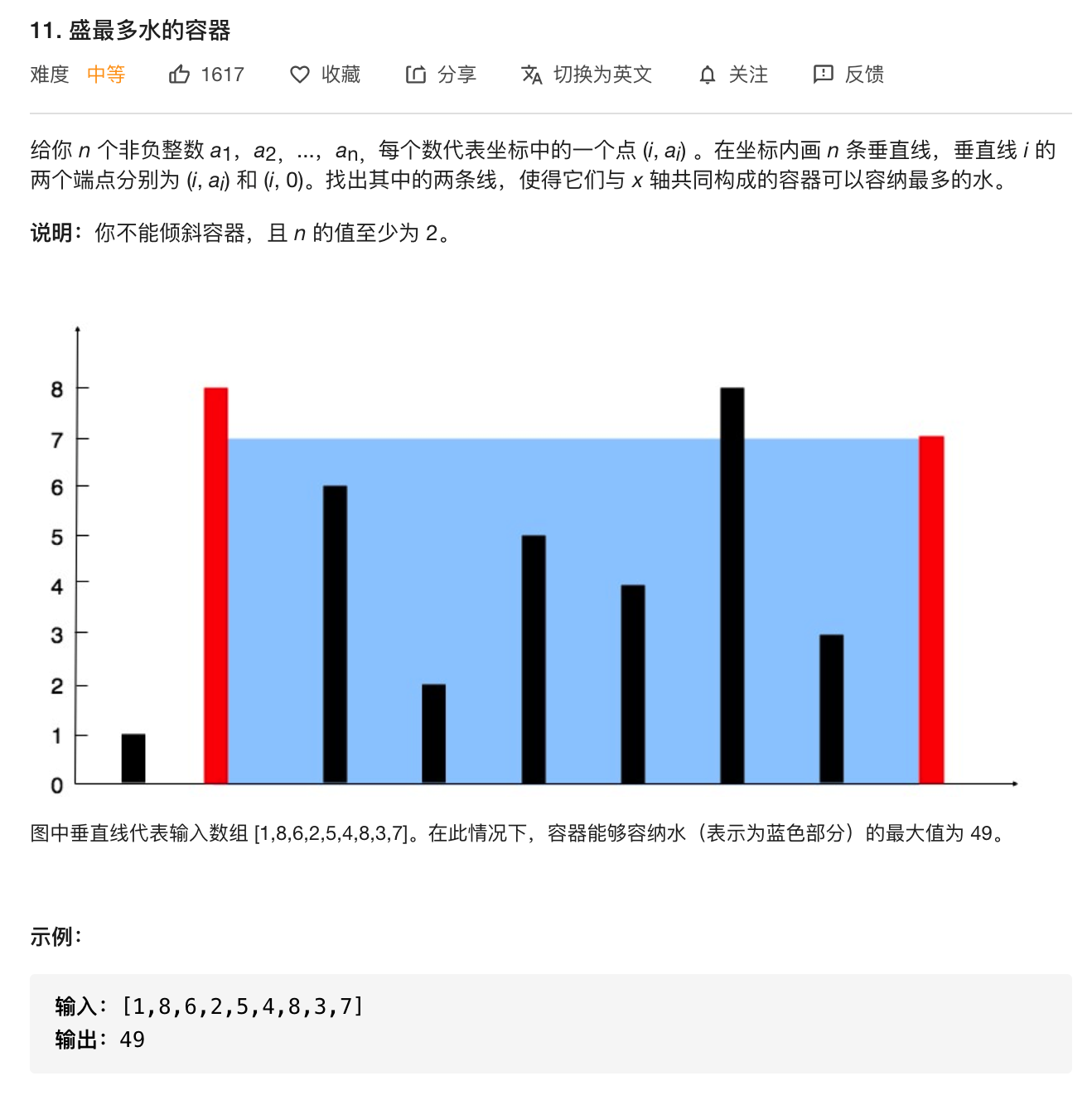
　　容积由两边的距离 len 与较短边的长度 minH 决定，len 缩短时，minH 增长才有可能得到更大的 len*minH 。

　　因此，想获得比当前容积大的容积，需要向内移动较小的边。

　　贪心算法：

    public final int maxArea(int[] height) {
        int begin = 0;
        int end = height.length - 1;
        int max = 0;
        while (begin < end) {
            max = Math.max(max, (end - begin) * Math.min(height[begin], height[end]));
            if (height[begin] > height[end]) {
                end--;
            } else {
                begin++;
            }
        }
        return max;
    }

　　双指针实现贪心，时间复杂度 O(N) 。