在leetcode刷到两数之和、三数之和、四数之和的问题,发现题解都在使用滑动窗口、双指针的方法,在此补充一下递归与递推的解题思路(因为我的解题思路都是思考解空间-遍历解空间-聪明的遍历解空间-发现方法到达优化瓶颈,再思考其它方式如双指针、hash等,对递归和递推总有执念)。
注:递归解法往往效率不高,本文仅是给出以递归的思路思考问题的过程以供参考,并不是题目的最优解法。

以四数之和为例,我们先看题目:

题目中不难发现,问题本身是带有递归结构的。可以用递归解决的问题大致包含以下三类:
(1)多重循环(递归层数不确定):N皇后问题
(2)本身用递归形式定义的问题:阶乘、波兰表达式
(3)将问题分解成规模更小的子问题:汉诺塔
我们在定义函数时,如果确定了问题具有递归结构,只需考虑回归条件和每一层与下层的关系,状态转移方程就是描述相邻层级间关系的函数,即如何用小问题的解来解决相邻层级的高层问题。我们定义函数f(x,target)为输出目标数组中x个和为target的元素,那么,f(4)与f(3)的关系为:
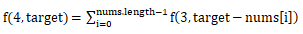
f(3)与f(2)的关系为:
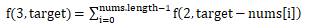
f(n)与f(n-1)的关系为:
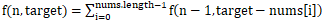
将状态转移方程用伪代码描述(不太喜欢内嵌代码的风格,完整代码在文末提供):
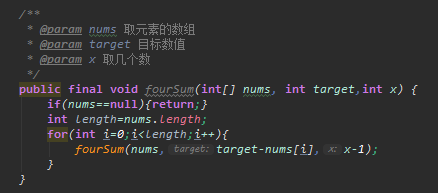
状态转移方程有了,我们还需要思考一下递归的回归条件。递归为用自身表示自身,不断的调用自己来求出自己的解,我们需要有一个最初始的条件(规模最小的子问题)来阻止函数无休止的调用自己。
在本问题中,终止条件非常明确,我们要求四数之和,在f(n,target)函数中,n的取值范围为1-4。当x=1时问题规模达到最小,此时无论是否得到了想要的结果我们都应该阻止继续向下递归。因此递归的回归条件为x=1,在问题到达回归条件时,我们应当判断是否得到了想要的解,在得到解时放入结果集或在未得到解时终止向下递归,尝试其它可能。
回归条件的伪代码处理如下(不太喜欢内嵌代码的风格,完整代码在文末提供):
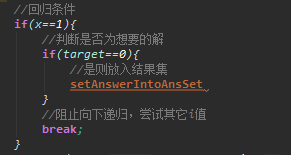
有了状态转移方程以及回归条件,我们得出了最简易版本的代码,此时我们进行一下填充,添加必要的变量及处理代码使其可以正常运行,这里我采用了栈结构来保存临时结果,方便在每一次尝试后回溯临时结果集中该次尝试存储的临时元素(不太喜欢内嵌代码的风格,完整代码在文末提供):
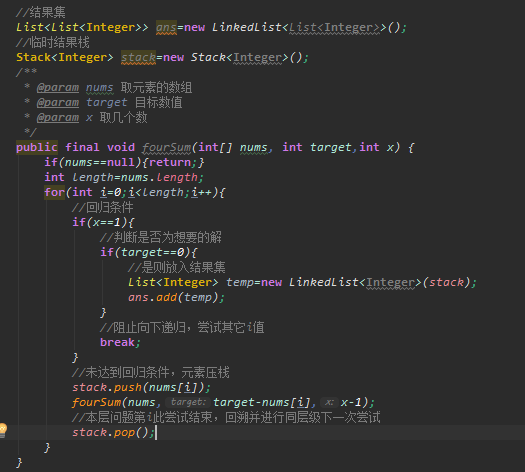
此时代码已经可以正常运行了,我们得到了最原始的递归函数。但还漏了题目中的一个条件:结果中不能有重复项。我们在上述代码的基础上对重复项进行处理。
重复项出现的原因是我们在对每一层级进行处理时都遍历了所有可能,同一层级在进行遍历时,后面的元素与前面元素组合的路径其实在遍历前面元素时已经走过了,如下图所示:

图中展示了递归的第一层和第二层中的部分。可以看出,在遍历第一层的第二个元素0时所走的路径中,0-1的组合在遍历元素1时已走过,即1-0。在此基础上,我们可以通过将上层的i值传递到下层进行剪枝来避免重复路径的出现:

进一步优化,此时,我们对解空间的遍历已近不会再走相同的路径,但是重复项依然会存在。原因是原数组nums中存在重复元素,我们虽然走了不同的路径,但因为重复元素的存在,我们会得到路径不同但实质值相同的解!如[1,0,-1,0,2,-2]中,我们第一个元素与第二个元素、第一个元素与第三个元素虽然为解空间中不同的路径,但得到的都是1-0。
此时我们可以对原数组进行排序,使实质相同的解中元素的排序相同,然后在将解加入解空间时进行contains判断,下面是最终代码,感兴趣的小伙伴可以跑跑看:
package learning; import java.util.*; /** * @Author Nyr * @Date 2019/11/15 14:52 * @Description leetcode四数之和 */ public class fourSum { //结果集 static List<List<Integer>> ans = new LinkedList<List<Integer>>(); //已用过的元素索引缓存,防止重复使用元素 static List<Integer> indexSet = new LinkedList<Integer>(); //临时结果栈 static Stack<Integer> stack = new Stack<Integer>(); public final static List<List<Integer>> fourSum(int[] nums, int target, int x, int beforeI) { if (nums == null) { return ans; } int length = nums.length; //剪枝,去重 for (int i = 0; i < length; i++) { //回归条件,凑齐四个元素,阻止向下递归并检查是否和为target if (x == 4) { if (target == 0) { //放入结果集 List<Integer> temp = new LinkedList<Integer>(stack); if (!ans.contains(temp)) { ans.add(temp); } } break; } //剪枝 if (i < beforeI) { continue; } //不重复使用同一元素 if (indexSet.contains(i)) { continue; } //递归深度不到4,压栈 stack.push(nums[i]); indexSet.add(i); //递归调用,问题抛给下一层 fourSum(nums, target - nums[i], x + 1, i); //本层问题第i此尝试结束,回溯并进行同层级下一次尝试 stack.pop(); indexSet.remove(x); } return ans; } public static void main(String[] args) { int[] nums = {1, 0, -1, 0, -2, 2};
//排序原数组 Arrays.sort(nums); fourSum(nums, 0, 0, 0); System.out.println(ans.toString()); } }