数组:很简单,数组用一块连续的内存空间,来存储相同类型的一组数据,最大的特点就是支持随机访问,用下标随机访问时间复杂的为O(1),但插入、删除操作也因此变得比较低效,平均情况时间复杂度为 O(n)。在平时的业务开发中,我们可以直接使用编程语言提供的容器类,比如 java的ArrayList ,就是用的动态数组,但是,如果是特别底层的开发,直接使用数组可能会更合适。
放下数组常用的冒泡排序方式和二分查找 java 代码。todo//快排
public class BlackTest { public static void main(String[] args) { // List<String> strings=new ArrayList<>(); int[] arr = {4,3,5,1,7,9,3}; bubbleSort(arr); System.out.println(search(arr,9)); } //冒泡排序 两个相邻的比较 public static void bubbleSort(int[] arr) { int temp;//定义一个临时变量 for(int i=0;i<arr.length-1;i++){//冒泡趟数 for(int j=0;j<arr.length-i-1;j++){ //如果顺序不对,则交换两个元素 if(arr[j+1]<arr[j]){ temp = arr[j]; arr[j] = arr[j+1]; arr[j+1] = temp; } } } } //二分查找 public static int search(int[] arr, int key) { int start = 0; int end = arr.length - 1; while (start <= end) { int middle = (start + end) / 2; if (key < arr[middle]) { end = middle - 1; } else if (key > arr[middle]) { start = middle + 1; } else { return middle; } } return -1; } }
解析java ArrayList源码分析//todo
链表:
它跟数组一样,也是非常基础、非常常用的数据结构。不过链表要比数组稍微复杂,从普通的单链表衍生出来好几种链表结构,比如双向链表、循环链表、双向循环链表。
和数组相比,链表更适合插入、删除操作频繁的场景,查询的时间复杂度较高。不过,在具体软件开发中,要对数组和链表的各种性能进行对比,综合来选择使用两者中的哪一个。
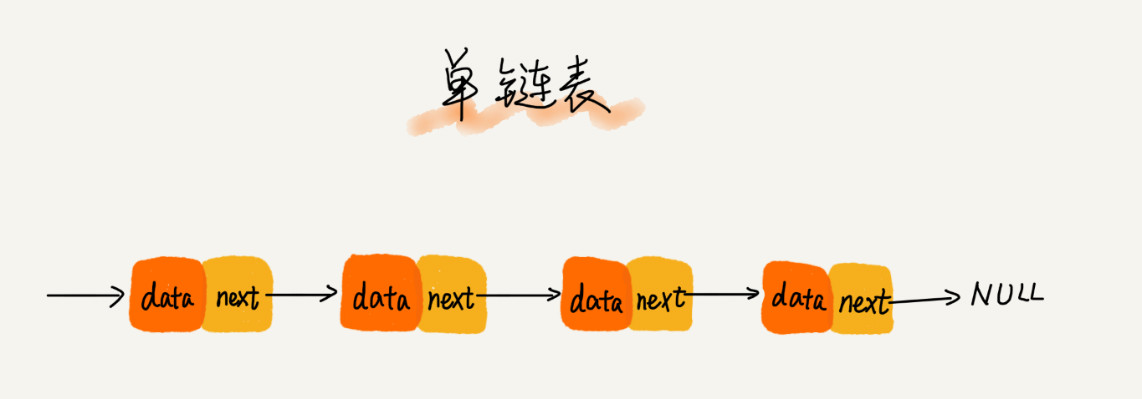
它的数据结构是不需要像数组一样有连续内存,只要有指针指到下一个内存卡就可以。如下:我们习惯性地把第一个结点叫作头结点,把最后一个结点叫作尾结点。其中,头结点用来记录链表的基地址。有了它,我们就可以遍历得到整条链表。而尾结点特殊的地方是:指针不是指向下一个结点,而是指向一个空地址 NULL,表示这是链表上最后一个结点。
栈:
总体来说就是先入后出。和洗盘子道理一样。
栈既可以用数组来实现,也可以用链表来实现。用数组实现的栈,我们叫作顺序栈,用链表实现的栈,我们叫作链式栈。
有个问题:VM 内存管理中有个“堆栈”的概念。栈内存用来存储局部变量和方法调用,堆内存用来存储 Java 中的对象。那 JVM 里面的“栈”跟我们这里说的“栈”是不是一回事呢?如果不是,那它为什么又叫作“栈”呢?
内存中的堆栈和数据结构堆栈不是一个概念,可以说内存中的堆栈是真实存在的物理区,数据结构中的堆栈是抽象的数据存储结构。
内存空间在逻辑上分为三部分:代码区、静态数据区和动态数据区,动态数据区又分为栈区和堆区。
代码区:存储方法体的二进制代码。高级调度(作业调度)、中级调度(内存调度)、低级调度(进程调度)控制代码区执行代码的切换。
静态数据区:存储全局变量、静态变量、常量,常量包括final修饰的常量和String常量。系统自动分配和回收。
栈区:存储运行方法的形参、局部变量、返回值。由系统自动分配和回收。
堆区:new一个对象的引用或地址存储在栈区,指向该对象存储在堆区中的真实数据。
队列:
队列最大的特点就是先进先出,主要的两个操作是入队和出队。跟栈一样,它既可以用数组来实现,也可以用链表来实现。用数组实现的叫顺序队列,用链表实现的叫链式队列。特别是长得像一个环的循环队列。在数组实现队列的时候,会有数据搬移操作,要想解决数据搬移的问题,我们就需要像环一样的循环队列。几种高级的队列结构,阻塞队列、并发队列,底层都还是队列这种数据结构,只不过在之上附加了很多其他功能。阻塞队列就是入队、出队操作可以阻塞,并发队列就是队列的操作多线程安全。
对于大部分资源有限的场景,当没有空闲资源时,基本上都可以通过“队列”这种数据结构来实现请求排队。如线程池数据库连接池,一般最好是用数组实现的队列,超过排队的队列大小就拒绝。毕竟用链表实现的话会是无界队列,会造成排队等待请求的时间过长。
散列表
其实就是hash表,散列表用的是数组支持按照下标随机访问数据的特性,所以散列表其实就是数组的一种扩展,由数组演化而来。可以说,如果没有数组,就没有散列表。
很好的例子 就是一些数字 通过has函数得到has 值存在数组中。
三点散列函数设计的基本要求:
散列函数计算得到的散列值是一个非负整数; 因为数组的下标值从0开始
如果 key1 = key2,那 hash(key1) == hash(key2);
如果 key1 ≠ key2,那 hash(key1) ≠ hash(key2)。能达到这种效果是很难的。这个要求看起来合情合理,但是在真实的情况下,要想找到一个不同的 key 对应的散列值都不一样的散列函数,几乎是不可能的。即便像业界著名的MD5、SHA、CRC等哈希算法,也无法完全避免这种散列冲突。而且,因为数组的存储空间有限,也会加大散列冲突的概率。
解决散列冲突的方法主要是链表法,和开放寻找法
二叉树
非线性表结构了
先说下树的基本概念
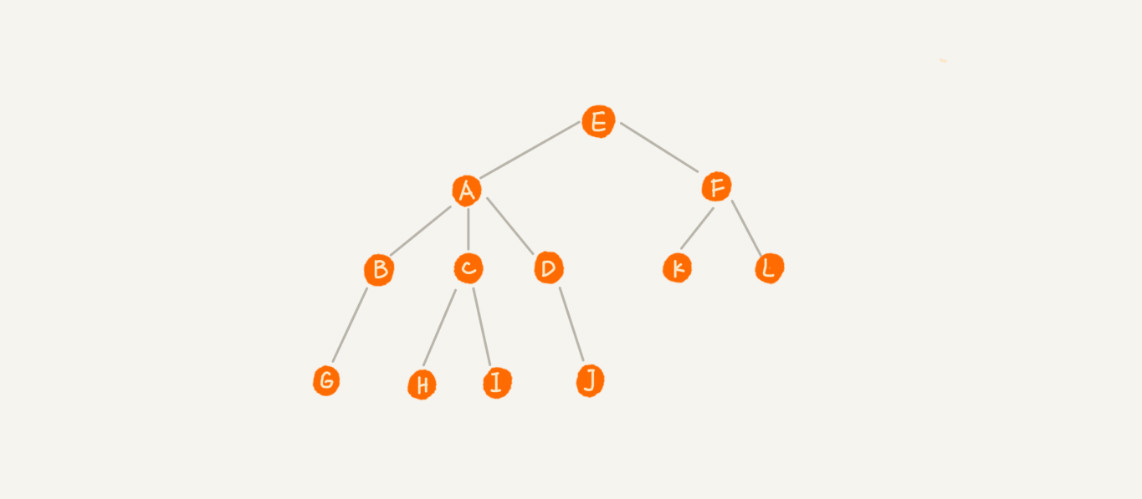
A 节点就是 B 节点的父节点,B 节点是 A 节点的子节点。B、C、D 这三个节点的父节点是同一个节点,所以它们之间互称为兄弟节点。我们把没有父节点的节点叫做根节点,也就是图中的节点 E。我们把没有子节点的节点叫做叶子节点或者叶节点,比如图中的 G、H、I、J、K、L 都是叶子节点
高度 深度 层数

二叉树 了
二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只有左子节点,有的节点只有右子节点
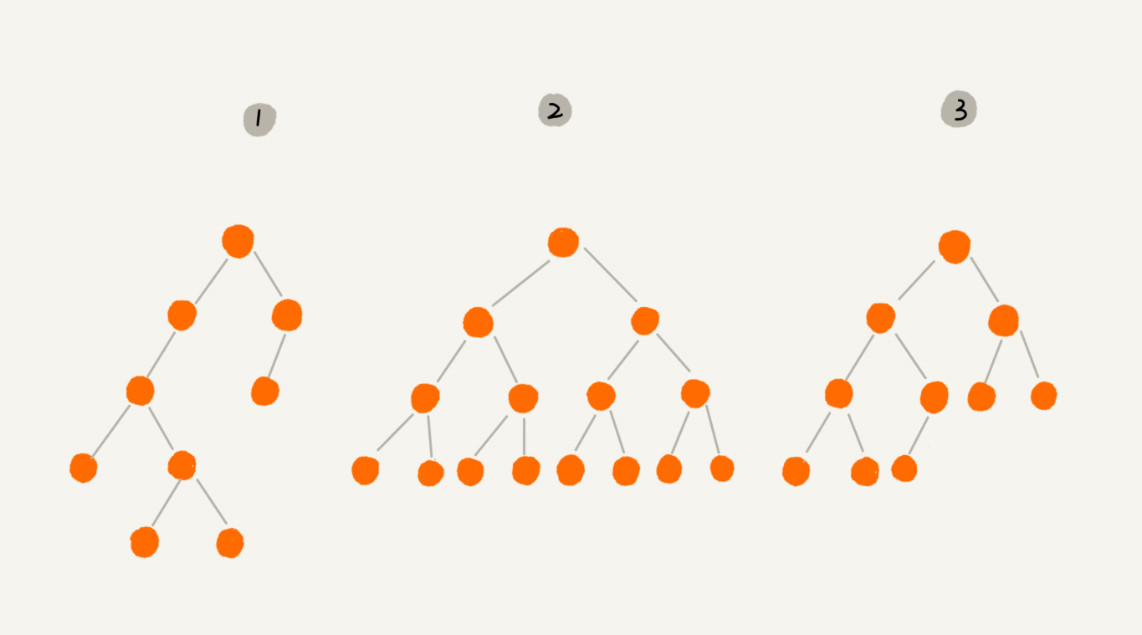
其中,编号 2 的二叉树中,叶子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个子节点,这种二叉树就叫做满二叉树。编号 3 的二叉树中,叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大,这种二叉树叫做完全二叉树。
二叉树既可以用链式存储,也可以用数组顺序存储。数组顺序存储的方式比较适合完全二叉树,其他类型的二叉树用数组存储会比较浪费存储空间。除此之外,二叉树里非常重要的操作就是前、中、后序遍历操作,遍历的时间复杂度是 O(n),你需要理解并能用递归代码来实现。
红黑树
为什么工程中都喜欢用红黑树,而不是其他平衡二叉查找树呢?
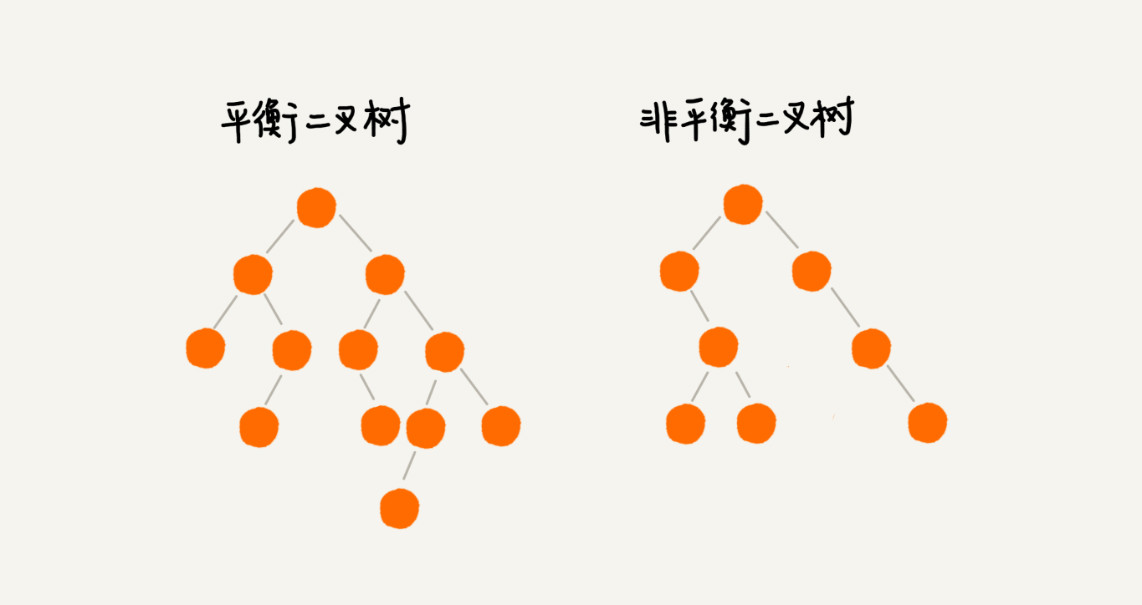
什么是“平衡二叉查找树”?平衡二叉树的严格定义是这样的:二叉树中任意一个节点的左右子树的高度相差不能大于 1。从这个定义来看,上一节我们讲的完全二叉树、满二叉树其实都是平衡二叉树,但是非完全二叉树也有可能是平衡二叉树
红黑树的英文是“Red-Black Tree”,简称 R-B Tree。它是一种不严格的平衡二叉查找树,我前面说了,它的定义是不严格符合平衡二叉查找树的定义的。那红黑树究竟是怎么定义的呢?
顾名思义,红黑树中的节点,一类被标记为黑色,一类被标记为红色。除此之外,一棵红黑树还需要满足这样几个要求:
根节点是黑色的;
每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据;
任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;
主要目的就是为了性能不退化 找到最平衡的方式
我们前面也讲到,平衡二叉查找树的初衷,是为了解决二叉查找树因为动态更新导致的性能退化问题。所以,“平衡”的意思可以等价为性能不退化。“近似平衡”就等价为性能不会退化得太严重。我们在上一节讲过,二叉查找树很多操作的性能都跟树的高度成正比。一棵极其平衡的二叉树(满二叉树或完全二叉树)的高度大约是 log2n,所以如果要证明红黑树是近似平衡的,我们只需要分析,红黑树的高度是否比较稳定地趋近 log2n 就好了。
//总之更加好用 近似平衡
红黑树是一种平衡二叉查找树。它是为了解决普通二叉查找树在数据更新的过程中,复杂度退化的问题而产生的。红黑树的高度近似 log2n,所以它是近似平衡,插入、删除、查找操作的时间复杂度都是 O(logn)。
我们刚刚提到了很多平衡二叉查找树,现在我们就来看下,为什么在工程中大家都喜欢用红黑树这种平衡二叉查找树?我们前面提到 Treap、Splay Tree,绝大部分情况下,它们操作的效率都很高,但是也无法避免极端情况下时间复杂度的退化。尽管这种情况出现的概率不大,但是对于单次操作时间非常敏感的场景来说,它们并不适用。AVL 树是一种高度平衡的二叉树,所以查找的效率非常高,但是,有利就有弊,AVL 树为了维持这种高度的平衡,就要付出更多的代价。每次插入、删除都要做调整,就比较复杂、耗时。所以,对于有频繁的插入、删除操作的数据集合,使用 AVL 树的代价就有点高了。红黑树只是做到了近似平衡,并不是严格的平衡,所以在维护平衡的成本上,要比 AVL 树要低。所以,红黑树的插入、删除、查找各种操作性能都比较稳定。对于工程应用来说,要面对各种异常情况,为了支撑这种工业级的应用,我们更倾向于这种性能稳定的平衡二叉查找树。