优先队列及堆排序
堆排序(Heap Sort)由威尔士-加拿大计算机科学家J. W. J. Williams在1964年发明,它利用了二叉堆(A binary heap)的性质实现了排序,并证明了二叉堆数据结构的可用性。同年,美国籍计算机科学家R. W. Floyd在其树排序研究的基础上,发布了一个改进的更好的原地排序的堆排序版本。
堆排序属于选择类排序算法。
一、优先队列
优先队列是一种能完成以下任务的队列:插入一个数值,取出最小或最大的数值(获取数值,并且删除)。
优先队列可以用二叉树来实现,我们称这种结构为二叉堆。
最小堆和最大堆是二叉堆的一种,是一颗完全二叉树(一种平衡树)。
最小堆的性质:
- 父节点的值都小于左右儿子节点。
- 这是一个递归的性质。
最大堆的性质:
- 父节点的值都大于左右儿子节点。
- 这是一个递归的性质。
最大堆和最小堆实现方式一样,只不过根节点一个是最大的,一个是最小的。
1.1. 最大堆特征
最大堆实现细节(两个操作):
- push:向堆中插入数据时,首先在堆的末尾插入数据,如果该数据比父亲节点还大,那么交换,然后不断向上提升,直到没有大小颠倒为止。
- pop:从堆中删除最大值时,首先把最后一个值复制到根节点上,并且删除最后一个数值,然后和儿子节点比较,如果值小于儿子,与儿子节点交换,然后不断向下交换, 直到没有大小颠倒为止。在向下交换过程中,如果有两个子儿子都大于自己,就选择较大的。
最大堆有两个核心操作,一个是上浮,一个是下沉,分别对应push和pop。
这是一个最大堆:
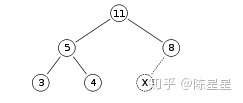
用数组表示为:[11 5 8 3 4]
1.2. 上浮操作
我们要往堆里push一个元素15,我们先把X = 15放到树最尾部,然后进行上浮操作。
因为15大于其父亲节点8,所以与父亲替换:
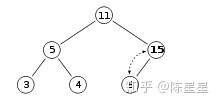
这时15还是大于其父亲节点11,继续替换:
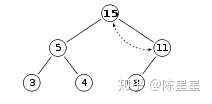
操作一次push的最好时间复杂度为:O(1),因为第一次上浮时如果不大于父亲,那么就结束了。最坏的时间复杂度为:O(logn),相当于每次都大于父亲,会一直往上浮到根节点,翻转次数等于树的高度,而树的高度等于元素个数的对数:log(n)。
1.3. 下沉操作
我们现在要将堆顶的元素pop出。如图我们要移除最大的元素11:
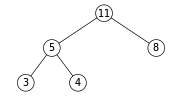
我们先将根节点移除,然后将最尾部的节点4放在根节点上:
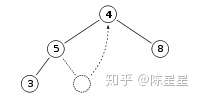
接着对根节点4进行下沉操作,与其两个儿子节点比较,发现较大的儿子节点8比4大,那么根节点4与其儿子节点8交换位置,向下翻转:
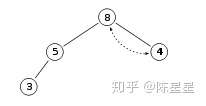
这样一直向下翻转就维持了最大堆的特征。
操作一次pop最好的时间复杂度也是:O(1),因为第一次比较时根节点就是最大的。最坏时间复杂度仍然是树的高度:O(logn)。
1.4. 时间复杂度分析
构建一个最大堆,从空堆开始,每次添加元素到尾部后,需要向上翻转,最坏翻转次数是:
第一次添加元素翻转次数:log1
第二次添加元素翻转次数:log2
第三次添加元素翻转次数:不大于log3的最大整数
第四次添加元素翻转次数:log4
第五次添加元素翻转次数:不大于log5的最大整数
...
第N次添加元素翻转次数:不大于logn的最大整数
近似 = log(1)+log(2)+log(3)+...+log(n) = log(n!)
从一个最大堆,逐一移除堆顶元素,然后将堆尾元素置于堆顶后,向下翻转恢复堆特征,最坏翻转次数是:
第一次移除元素恢复堆时间复杂度:logn
第二次移除元素恢复堆时间复杂度:不大于log(n-1)的最大整数
第三次移除元素恢复堆时间复杂度:不大于log(n-2)的最大整数
...
第N次移除元素恢复堆时间复杂度:log1
近似 = log(1)+log(2)+log(3)+...+log(n) = log(n!)
根据斯特林公式:
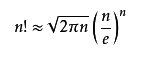
可以进行证明log(n!)和nlog(n)是同阶的:

所以构建一个最大堆的最坏时间复杂度是:O(nlogn)。
从堆顶一个个移除元素,直到移完,整个过程最坏时间复杂度也是:O(nlogn)。
从构建堆到移除堆,总的最坏复杂度是:O(nlogn)+O(nlogn),我们可以认为是:O(nlogn)。
如果所有的元素都一样的情况下,建堆和移除堆的每一步都不需要翻转,最好时间复杂度为:O(n),复杂度主要在于遍历元素。
如果元素不全一样,即使在建堆的时候不需要翻转,但在移除堆的过程中一定会破坏堆的特征,导致恢复堆时需要翻转。比如一个n个元素的已排好的序的数列,建堆时每次都满足堆的特征,不需要上浮翻转,但在移除堆的过程中最尾部元素需要放在根节点,这个时候导致不满足堆的特征,需要下沉翻转。因此,在最好情况下,时间复杂度仍然是:O(nlog)。
因此,最大堆从构建到移除,总的平均时间复杂度是:O(nlogn)。
1.5. 最大堆实现
// 一个最大堆,一颗完全二叉树
// 最大堆要求节点元素都不小于其左右孩子
type Heap struct {
// 堆的大小
Size int
// 使用内部的数组来模拟树
// 一个节点下标为 i,那么父亲节点的下标为 (i-1)/2
// 一个节点下标为 i,那么左儿子的下标为 2i+1,右儿子下标为 2i+2
Array []int
}
// 初始化一个堆
func NewHeap(array []int) *Heap {
h := new(Heap)
h.Array = array
return h
}
// 最大堆插入元素
func (h *Heap) Push(x int) {
// 堆没有元素时,使元素成为顶点后退出
if h.Size == 0 {
h.Array[0] = x
h.Size++
return
}
// i 是要插入节点的下标
i := h.Size
// 如果下标存在
// 将小的值 x 一直上浮
for i > 0 {
// parent为该元素父亲节点的下标
parent := (i - 1) / 2
// 如果插入的值小于等于父亲节点,那么可以直接退出循环,因为父亲仍然是最大的
if x <= h.Array[parent] {
break
}
// 否则将父亲节点与该节点互换,然后向上翻转,将最大的元素一直往上推
h.Array[i] = h.Array[parent]
i = parent
}
// 将该值 x 放在不会再翻转的位置
h.Array[i] = x
// 堆数量加一
h.Size++
}
// 最大堆移除根节点元素,也就是最大的元素
func (h *Heap) Pop() int {
// 没有元素,返回-1
if h.Size == 0 {
return -1
}
// 取出根节点
ret := h.Array[0]
// 因为根节点要被删除了,将最后一个节点放到根节点的位置上
h.Size--
x := h.Array[h.Size] // 将最后一个元素的值先拿出来
h.Array[h.Size] = ret // 将移除的元素放在最后一个元素的位置上
// 对根节点进行向下翻转,小的值 x 一直下沉,维持最大堆的特征
i := 0
for {
// a,b为下标 i 左右两个子节点的下标
a := 2*i + 1
b := 2*i + 2
// 左儿子下标超出了,表示没有左子树,那么右子树也没有,直接返回
if a >= h.Size {
break
}
// 有右子树,拿到两个子节点中较大节点的下标
if b < h.Size && h.Array[b] > h.Array[a] {
a = b
}
// 父亲节点的值都大于或等于两个儿子较大的那个,不需要向下继续翻转了,返回
if x >= h.Array[a] {
break
}
// 将较大的儿子与父亲交换,维持这个最大堆的特征
h.Array[i] = h.Array[a]
// 继续往下操作
i = a
}
// 将最后一个元素的值 x 放在不会再翻转的位置
h.Array[i] = x
return ret
}
以上为最大堆的实现。
三、普通堆排序
根据最大堆,堆顶元素一直是最大的元素特征,可以实现堆排序。
先构建一个最小堆,然后依次把根节点元素pop出即可:
func main() {
list := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
// 构建最大堆
h := NewHeap(list)
for _, v := range list {
h.Push(v)
}
// 将堆元素移除
for range list {
h.Pop()
}
// 打印排序后的值
fmt.Println(list)
}
输出:
1 3 4 5 6 6 6 8 9 14 25 49
根据以上最大堆的时间复杂度分析,从堆构建到移除最坏和最好的时间复杂度:O(nlogn),这也是堆排序的最好和最坏的时间复杂度。
这样实现的堆排序是普通的堆排序,性能不是最优的。
因为一开始会认为堆是空的,每次添加元素都需要添加到尾部,然后向上翻转,需要用Heap.Size来记录堆的大小增长,这种堆构建,可以认为是非原地的构建,影响了效率。
美国籍计算机科学家R. W. Floyd改进的原地自底向上的堆排序,不会从空堆开始,而是把待排序的数列当成一个混乱的最大堆,从底层逐层开始,对元素进行下沉操作,一直恢复最大堆的特征,直到根节点。
将构建堆的时间复杂度从O(nlogn)降为O(n),总的堆排序时间复杂度从O(2nlogn)改进到O(n+nlogn)。
三、自底向上堆排序
自底向上堆排序,仅仅将构建堆的时间复杂度从O(nlogn)改进到O(n),其他保持不变。
这种堆排序,不再每次都将元素添加到尾部,然后上浮翻转,而是在混乱堆的基础上,从底部向上逐层进行下沉操作,下沉操作比较的次数会减少。步骤如下:
- 先对最底部的所有非叶子节点进行下沉,即这些非叶子节点与它们的儿子节点比较,较大的儿子和父亲交换位置。
- 接着从次二层开始的非叶子节点重复这个操作,直到到达根节点最大堆就构建好了。
从底部开始,向上推进,所以这种堆排序又叫自底向上的堆排序。
为什么自底向上构建堆的时间复杂度是:O(n)。证明如下:
第k层的非叶子节点的数量为n/2^k,每一个非叶子节点下沉的最大次数为其子孙的层数:k,而树的层数为logn层,那么总的翻转次数计算如下:
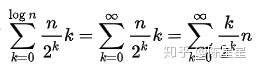
因为如下的公式是成立的:
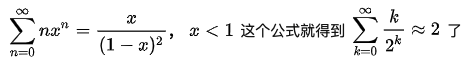
所以翻转的次数计算结果为:2n次。也就是构建堆的时间复杂度为:O(n)。
我们用非递归的形式来实现,非递归相对容易理解:
package main
import "fmt"
// 先自底向上构建最大堆,再移除堆元素实现堆排序
func HeapSort(array []int) {
// 堆的元素数量
count := len(array)
// 最底层的叶子节点下标,该节点位置不定,但是该叶子节点右边的节点都是叶子节点
start := count/2 + 1
// 最后的元素下标
end := count - 1
// 从最底层开始,逐一对节点进行下沉
for start >= 0 {
sift(array, start, count)
start-- // 表示左偏移一个节点,如果该层没有节点了,那么表示到了上一层的最右边
}
// 下沉结束了,现在要来排序了
// 元素大于2个的最大堆才可以移除
for end > 0 {
// 将堆顶元素与堆尾元素互换,表示移除最大堆元素
array[end], array[0] = array[0], array[end]
// 对堆顶进行下沉操作
sift(array, 0, end)
// 一直移除堆顶元素
end--
}
}
// 下沉操作,需要下沉的元素时 array[start],参数 count 只要用来判断是否到底堆底,使得下沉结束
func sift(array []int, start, count int) {
// 父亲节点
root := start
// 左儿子
child := root*2 + 1
// 如果有下一代
for child < count {
// 右儿子比左儿子大,那么要翻转的儿子改为右儿子
if count-child > 1 && array[child] < array[child+1] {
child++
}
// 父亲节点比儿子小,那么将父亲和儿子位置交换
if array[root] < array[child] {
array[root], array[child] = array[child], array[root]
// 继续往下沉
root = child
child = root*2 + 1
} else {
return
}
}
}
func main() {
list := []int{5, 9, 1, 6, 8, 14, 6, 49, 25, 4, 6, 3}
HeapSort(list)
// 打印排序后的值
fmt.Println(list)
}
输出:
[1 3 4 5 6 6 6 8 9 14 25 49]
系列文章入口
我是陈星星,欢迎阅读我亲自写的 数据结构和算法(Golang实现),文章首发于 阅读更友好的GitBook。
- 数据结构和算法(Golang实现)(1)简单入门Golang-前言
- 数据结构和算法(Golang实现)(2)简单入门Golang-包、变量和函数
- 数据结构和算法(Golang实现)(3)简单入门Golang-流程控制语句
- 数据结构和算法(Golang实现)(4)简单入门Golang-结构体和方法
- 数据结构和算法(Golang实现)(5)简单入门Golang-接口
- 数据结构和算法(Golang实现)(6)简单入门Golang-并发、协程和信道
- 数据结构和算法(Golang实现)(7)简单入门Golang-标准库
- 数据结构和算法(Golang实现)(8.1)基础知识-前言
- 数据结构和算法(Golang实现)(8.2)基础知识-分治法和递归
- 数据结构和算法(Golang实现)(9)基础知识-算法复杂度及渐进符号
- 数据结构和算法(Golang实现)(10)基础知识-算法复杂度主方法
- 数据结构和算法(Golang实现)(11)常见数据结构-前言
- 数据结构和算法(Golang实现)(12)常见数据结构-链表
- 数据结构和算法(Golang实现)(13)常见数据结构-可变长数组
- 数据结构和算法(Golang实现)(14)常见数据结构-栈和队列
- 数据结构和算法(Golang实现)(15)常见数据结构-列表
- 数据结构和算法(Golang实现)(16)常见数据结构-字典
- 数据结构和算法(Golang实现)(17)常见数据结构-树
- 数据结构和算法(Golang实现)(18)排序算法-前言
- 数据结构和算法(Golang实现)(19)排序算法-冒泡排序
- 数据结构和算法(Golang实现)(20)排序算法-选择排序
- 数据结构和算法(Golang实现)(21)排序算法-插入排序
- 数据结构和算法(Golang实现)(22)排序算法-希尔排序
- 数据结构和算法(Golang实现)(23)排序算法-归并排序
- 数据结构和算法(Golang实现)(24)排序算法-优先队列及堆排序
- 数据结构和算法(Golang实现)(25)排序算法-快速排序
- 数据结构和算法(Golang实现)(26)查找算法-哈希表
- 数据结构和算法(Golang实现)(27)查找算法-二叉查找树
- 数据结构和算法(Golang实现)(28)查找算法-AVL树
- 数据结构和算法(Golang实现)(29)查找算法-2-3树和左倾红黑树
- 数据结构和算法(Golang实现)(30)查找算法-2-3-4树和普通红黑树