回文树简述
在大部分说法中,回文树与回文自动机指的是一个东西;
回文树是对一个字符串,基于自动机思想构建的处理回文问题的树形结构;
回文树是对着一个单串建立的;
于是他主要用于计数(回文子串种类及个数)
基本建立思路是建立其前缀的回文树,然后每加上一个字符,统计产生了什么回文;
回文树存在fail指针但一般不承接字符串匹配问题;
(回文树大概可以判定一个回文串是不是一个串的子串,但KMP之类的可以做得更好)
构建好的回文树,是这样的:
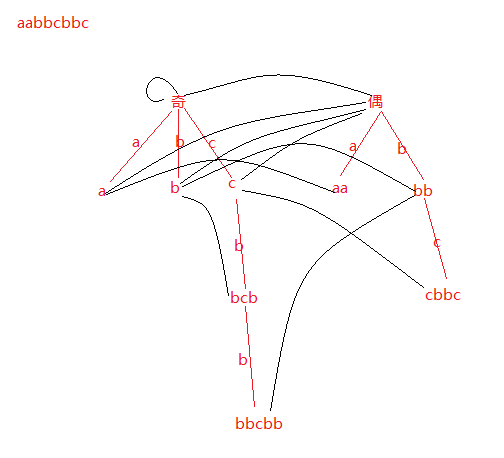
(好难看)
(点“偶”的fail指向点“奇”)
可看出:
存在两个树结构,分别记录奇数|偶数长度的回文;
每个点记录一种字符串(但是由于可以通过根到该节点的路径确定这个字符串是什么,于是并不需要真的在该节点记录/*写下*/这个信息)
每个节点连字符x边向一个子节点,表示在她的左右两边加x构成的回文是这个总字符串的子串(根节点相关部分单独定义);
每个节点连一条fail指针向其最长后缀回文;
几个性质
|s|表示s串的长度;
节点数不超过|s|:每个节点是互不相同的回文,每个回文都是某一个点的最长后缀回文,而每个点的最长后缀回文是唯一的;
转移数是O(|s|)级的:树有节点数-2个边(因为是两棵树),加上每个节点一个fail,于是是O(|s|)级的;
构造方法
回文树的基础插入算法:
建立s的回文树;
现在已建立了s的前缀x,然后考虑插入下一个字符;
每次插入最多只会把她的最长后缀回文贡献到树中;
证明:
c除最长后缀回文之外的后缀回文i是其最长后缀回文k的子串,则她关于k的中心有一个对称串j,由于k本身是对称的,于是j与i本质相同,由于j已经加入回文树中,于是i不必加入;
那么我们设x串之前的最长后缀回文是t,在加入c后,我们期望的c的最长后缀回文最长是ctc,
但t串前面不是字符c怎么办,
试试t的除自己外最长回文后缀的前一个字符是不是c,
若不行,再试试她的最长回文后缀。。。。
这样找的的回文如果还没存在与回文树中,则将其插入;
为了方便这一过程,我们维护每点一个指针fail,s当前的前缀x的最长回文后缀t,没有ctc,就跳fail,直到可以匹配;
建fail的过程与匹配过程类似;
然后维护一个last指向当前在的节点,以便插入新的回文;
通过势能分析法发现这个算法是每次插入均摊O(1),总共O(n)的;(反正我也不会)
例题
对读入的字符串,正反分别建回文树,在此同时分别记录以每个为起点|终点的最长前|后缀回文;
枚举断点,求最值即可;
1 #include<cstdio> 2 #include<cstring> 3 using namespace std; 4 struct dt{ 5 int ch[30],fail,len; 6 }; 7 struct Pld_T{ 8 int tot,last; 9 dt data[500500]; 10 int len[500500]; 11 char s[500500]; 12 void Init(){ 13 data[0].fail=1; 14 data[1].len=-1; 15 tot=1;last=0; 16 } 17 void insert(int x){ 18 int j; 19 while(s[x-data[last].len-1]!=s[x])last=data[last].fail; 20 if(!data[last].ch[s[x]-'a']){ 21 data[++tot].len=data[last].len+2; 22 j=data[last].fail; 23 while(s[x-data[j].len-1]!=s[x])j=data[j].fail; 24 data[tot].fail=data[j].ch[s[x]-'a']; 25 data[last].ch[s[x]-'a']=tot; 26 last=tot; 27 } 28 else 29 last=data[last].ch[s[x]-'a']; 30 len[x]=data[last].len; 31 } 32 }; 33 Pld_T pld_t1,pld_t2; 34 int main() 35 { 36 int i,j,k,len,ans=0; 37 pld_t1.Init();pld_t2.Init(); 38 scanf("%s",pld_t1.s+1); 39 len=strlen(pld_t1.s+1); 40 for(i=len,j=1;i>=1;i--,j++) 41 pld_t2.s[j]=pld_t1.s[i]; 42 pld_t2.s[0]=pld_t1.s[0]='#'; 43 pld_t2.s[len+1]=pld_t1.s[len+1]='�'; 44 for(i=1;i<=len;i++){ 45 pld_t1.insert(i); 46 pld_t2.insert(i); 47 } 48 for(i=1;i<len;i++) 49 if(ans<pld_t1.len[i]+pld_t2.len[len-i]) 50 ans=pld_t1.len[i]+pld_t2.len[len-i]; 51 printf("%d",ans); 52 return 0; 53 }
对每个点维护cnt表示她是几个字符的最长回文后缀;
那么他出现的次数就是她作为自己的末端字符的最长回文后缀出现的次数,以及她作为自己的末端字符的最长回文后缀的回文后缀(也不比是除她外最长的)出现的次数;
见代码
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 char s[300010]; 6 struct Pld_T{ 7 int ch[26],fail,len,cnt; 8 }; 9 Pld_T pld_t[300010]; 10 int tot; 11 int main() 12 { 13 int i,j,k,len; 14 long long ans=0; 15 scanf("%s",s+1); 16 len=strlen(s+1);s[0]='#'; 17 pld_t[0].fail=1;k=0;pld_t[1].len=-1;tot=1; 18 for(i=1;i<=len;i++){ 19 while(s[i-pld_t[k].len-1]!=s[i])k=pld_t[k].fail; 20 if(!pld_t[k].ch[s[i]-'a']){ 21 pld_t[++tot].len=pld_t[k].len+2; 22 j=pld_t[k].fail; 23 while(s[i-pld_t[j].len-1]!=s[i])j=pld_t[j].fail; 24 pld_t[tot].fail=pld_t[j].ch[s[i]-'a']; 25 pld_t[k].ch[s[i]-'a']=tot; 26 } 27 k=pld_t[k].ch[s[i]-'a']; 28 pld_t[k].cnt++; 29 } 30 for(i=tot;i>=2;i--){ 31 pld_t[pld_t[i].fail].cnt+=pld_t[i].cnt; 32 if((long long)pld_t[i].cnt*pld_t[i].len>ans) 33 ans=(long long)pld_t[i].cnt*pld_t[i].len; 34 } 35 printf("%lld",ans); 36 return 0; 37 }
我之前想在fail树上建LCT来着,呵呵呵哈哈哈哈!!!!!!!!!!