线性回归
本章内容
- 线性回归
- 局部加权线性回归
- 岭回归和逐步线性回归
- 预测鲍鱼年龄和乐高玩具价格
前面的章节给大家介绍了监督学习的分类部分,接下来几章将会带领同学们翱翔浩瀚的回归海洋,注意此回归不是 Logistic 回归(Logistic 回归之所以取名为这是因为历史遗留问题)。具体是什么,那就开始让我们来揭秘吧!
注意: 分类的目标变量是标称型数据;回归的目标变量是连续性数据。
用线性回归找到最佳拟合直线
- 线性回归的优缺点:
优点:结果易于理解,计算上不复杂
缺点:对非线性的数据拟合不好
适用数据类型:数值型和标称型数据 - 回归的目的:预测数值型的目标值
- 预测汽车功率大小的计算公式:
功率 = 0.0015 * 耗油量 + 0.99 * 百米加速时长 (纯属虚构,请勿模仿) - 回归方程:上述计算公式即回归方程
- 回归系数:上述计算公式中的0.0015和0.99
- 预测值:给定所有待输入的特征值乘以对应的回归系数的总和
- 非线性回归:输出为输入的乘积,例:功率 = 0.0015 * 耗油量 * 百米加速时长
- 回归的一般方法:
- 收集数据:采用任意方法收集数据
- 准备数据:回归需要数值型数据,标称型数据将被转成数值型数据
- 分析数据:可视化数据,采用缩减法求得新回归系数后绘图再与上一张图比较
- 训练算法:找到合适的回归系数
- 测试算法:使用 R^2^或者预测值和数据的拟合度,来分析模型的效果
- 使用算法:使用回归预测连续性数据的类别标签
- 矩阵x:输入的所有数据
- 向量 w:与数据对应的回归系数
- 预测结果 Y~1~:(Y_1={X^T}_1w)
- 平方误差:(sum_{i=1}^m(y_i-{x^T}_iw)^2)
- 矩阵表示平方误差:((y-Xw)^T(y-Xw))
- 平方误差对 w 求导:(X^T(Y-Xw))
- 平方误差对 w 求导等于零得:(hat{w}=(X^TX)-1X^Ty)
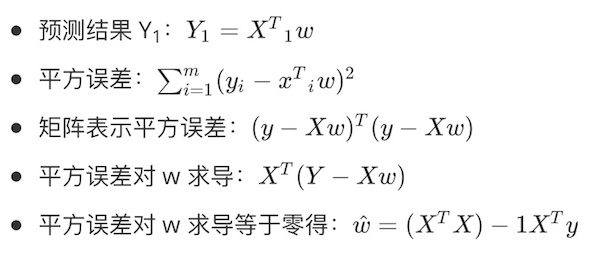
- w 上方的标记含义:当前可以估计出 w 的最优解,即 w 的一个最佳估计
- 上述公式包含((X^TX)^{-1}),即该方程中的 X 必须存在逆矩阵
注意:不要纠结于公式,这不会影响你学习机器学习
程序8-1 标准回归函数和数据导入函数
# coding: 'utf-8'
import os
import numpy as np
import matplotlib.pyplot as plt
from path_settings import machine_learning_PATH
data_set_path = os.path.join(machine_learning_PATH, '第八章/data-set')
ex0_path = os.path.join(data_set_path, 'ex0.txt')
ex1_path = os.path.join(data_set_path, 'ex1.txt')
abalone_path = os.path.join(data_set_path, 'abalone.txt')
def load_data_set(filename):
# 文本第一行值全为0的解释:简单说是因为两个矩阵相乘一个矩阵的行和另一个矩阵的列得相等,具体可查资料
num_feat = len(open(filename).readline().split(' ')) - 1
data_mat = []
label_mat = []
fr = open(filename)
for line in fr.readlines():
line_arr = []
cur_line = line.strip().split(' ')
for i in range(num_feat):
line_arr.append(float(cur_line[i]))
data_mat.append(line_arr)
label_mat.append(float(cur_line[-1]))
return data_mat, label_mat
def stand_regres(x_arr, y_arr):
x_mat = np.mat(x_arr)
y_mat = np.mat(y_arr)
x_tx = x_mat.T * x_mat
# 判断矩阵是否为奇异矩阵,即矩阵是否有逆矩阵
if np.linalg.det(x_tx) == 0:
print("奇异矩阵没有逆矩阵")
return
ws = x_tx.I * (x_mat.T * y_mat.T)
# 求解未知矩阵
# ws = np.linalg.solve(x_tx,x_mat.T*y_mat.T)
return x_mat, y_mat, ws
def test_stand_regres():
x_arr, y_arr = load_data_set(ex0_path)
_, _, ws = stand_regres(x_arr, y_arr)
print(ws)
if __name__ == '__main__':
test_stand_regres()
程序8-2 基于程序8-1绘图
def plot_stand_regres(x_mat, y_mat, ws):
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(x_mat[:, 1].flatten().A[0], y_mat.T[:, 0].flatten().A[0])
x_copy = x_mat.copy()
x_copy.sort(0)
y_hat = x_copy * ws
ax.plot(x_copy[:, 1], y_hat)
plt.show()
def test_plot_stand_regres():
x_arr, y_arr = load_data_set(ex0_path)
x_mat, y_mat, ws = stand_regres(x_arr, y_arr)
plot_stand_regres(x_mat, y_mat, ws)
# 判断拟合效果
print(np.corrcoef((x_mat * ws).T, y_mat))
'''
[[1. 0.98647356]
[0.98647356 1. ]]
'''
if __name__ == '__main__':
# test_stand_regres()
test_plot_stand_regres()
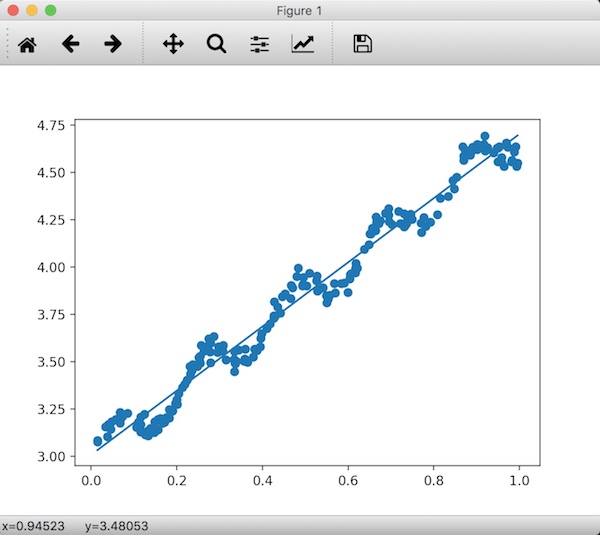
图片8-1 ex0的数据集和它的最佳拟合直线
局部加权线性回归
-
局部加权线性回归:给待预测点附近的每个点赋予一定的权重
-
局部加权线性回归求回归系数公式:(hat{w}=(X^TWX)^{-1}X^TWy)
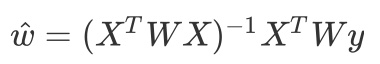
-
W:给每个数据点赋予权重的矩阵
-
LWLR使用“核”(类似于支持向量机中的核)来对附近的点赋予更高的权重。
-
最常用的核——高斯核:(w(i,i)=expleft({frac{|x^{(i)}-x|}{-2k^2}} ight))
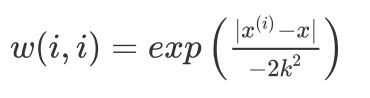
-
点 x 与 x(i)越近,w(i,i)将会越大,参数 k 决定了对附近的点赋予多大的权重。
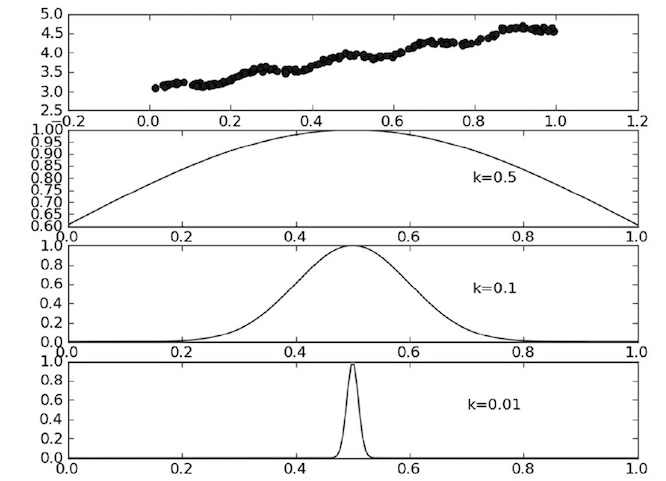
图片8-2 参数k与权重的关系
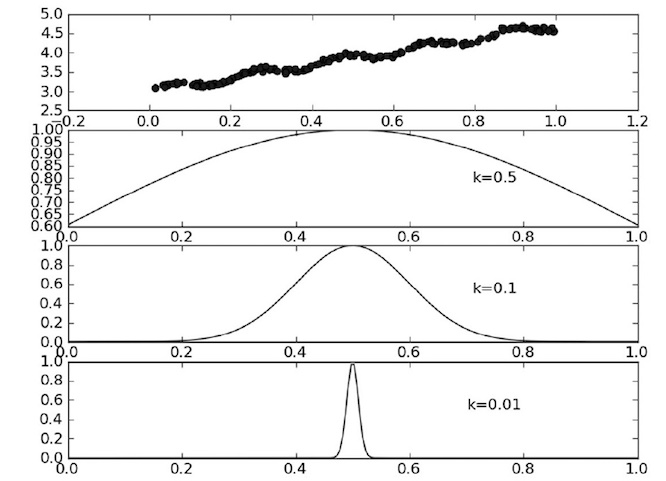
- 假定我们正预测的点是 x=0.5,最上面的是原始数据集,第二个图显示了当 k=0.5 时,大部分数据都用于训练回归模型;最下面的图显示当 k=0.01 时,仅有很少的局部点被用于训练回归模型。
程序8-3 局部加权线性回归函数
def lwlr(test_point, x_arr, y_arr, k=1):
"""给样本点增加权重,参数 k 控制衰减的速度"""
x_mat = np.mat(x_arr)
y_mat = np.mat(y_arr)
m = np.shape(x_mat)[0]
# 创建对角权重矩阵。该矩阵对角线元素全为1,其余元素全为0
weights = np.mat(np.eye(m))
for j in range(m):
diff_mat = test_point - x_mat[j, :]
weights[j, j] = np.exp(diff_mat * diff_mat.T / (-2 * k ** 2))
x_tx = x_mat.T * (weights * x_mat)
if np.linalg.det(x_tx) == 0:
print("奇异矩阵没有逆矩阵")
return
ws = x_tx.I * (x_mat.T * (weights * y_mat.T))
return test_point * ws
def lwlr_test(test_arr, x_arr, y_arr, k=1):
"""使数据集中每个点调用 lwlr 方法"""
m = np.shape(test_arr)[0]
y_hat = np.zeros(m)
for i in range(m):
y_hat[i] = lwlr(test_arr[i], x_arr, y_arr, k)
return y_hat
def test_lwlr_test():
x_arr, y_arr = load_data_set(ex0_path)
y_hat = lwlr_test(x_arr, x_arr, y_arr, 0.003)
print(y_hat)
def plot_lwlr(x_sort, y_hat, str_ind, x_mat, y_mat):
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(x_sort[:, 1], y_hat[str_ind])
ax.scatter(x_mat[:, 1].flatten().A[0], y_mat.T[:, 0].flatten().A[0], s=2, c='red')
plt.show()
def test_plot_lwlr():
x_arr, y_arr = load_data_set(ex0_path)
x_mat = np.mat(x_arr)
y_mat = np.mat(y_arr)
y_hat = lwlr_test(x_arr, x_arr, y_arr, 0.01)
str_ind = x_mat[:, 1].argsort(0)
x_sort = x_mat[str_ind][:, 0, :]
plot_lwlr(x_sort, y_hat, str_ind, x_mat, y_mat)
if __name__ == '__main__':
# test_stand_regres()
# test_plot_stand_regres()
# test_lwlr_test()
test_plot_lwlr()
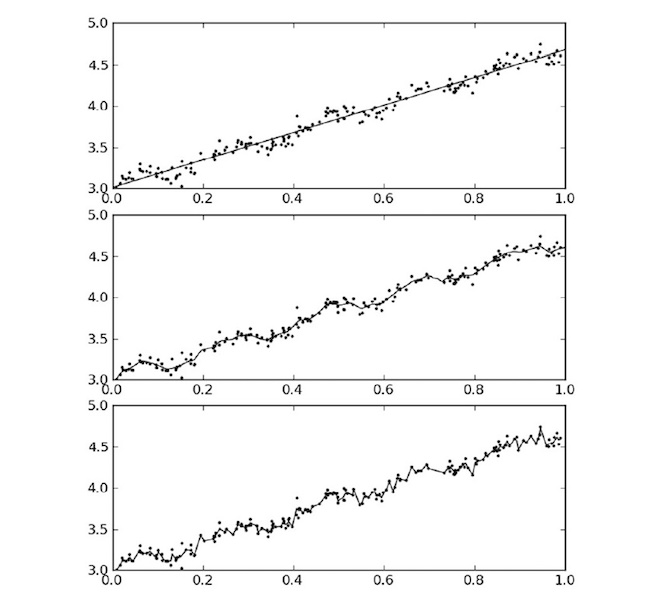
图片8-3 局部加权线性回归结果
示例:预测鲍鱼的年龄
缩减系数来“理解”数据
岭回归
前向逐步回归
权衡偏差与方差
示例:预测乐高玩具套装的价格
收集数据:使用 Google 购物的 API
训练算法:建立模型
本章小结
线性回归和局部加权线性回归
由于看完《机器学习实战》第八章中的局部加权线性回归后,敲完代码之后只是知道它是这样的,但不是很清楚内在的原因。书中并没有对其做过多解释,百度也找不到一篇很好的文章来解释 线性回归和局部加权线性回归 两者之间的区别。索性写一写自己对 线性回归和局部加权线性回归 的看法与感悟。也许还是不那么准确,但一定是清晰易懂的。
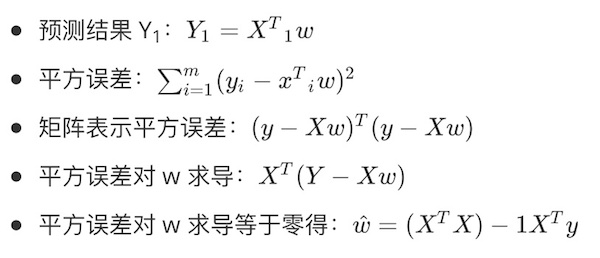
其中的平方误差是我们的在 x=x~i~ 上预测值与实际值的差值平方,而我们需要做的任务就是找到一个最合适的 w 使得该差值平方最小。
再来说说我们的局部加权线性回归(LWLR),它只是在线性回归的基础上加了一个权重,而LWLR通常使用“核”(类似于自持向量机中的核)来对附近的点赋予更高的权重。因此它的公式变成:
(sum_{i=1}^mW_i(y_i-x^T_iw)^2)
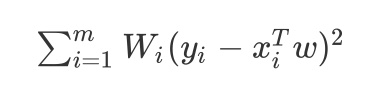
注意:W~i~ 是赋予 x~i~ 权重的矩阵,也可以是向量。
一般我们的 W~i~ 最常用的核是高斯核:(w(i,i)=expleft({frac{|x^{(i)}-x|}{-2k^2}} ight))
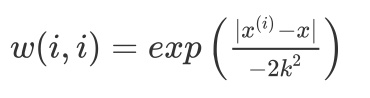
注意:高斯核中的 x 为新预测样本的特征数据即新的 x,它同 w 也是一个向量,参数 k 控制了权值变化的速率。
以上介绍了局部加权线性回归的理论,现在通过图像我们再来形象化的解释局部加权线性回归。首先看看不同 k 下的参数 k 与权重的关系:
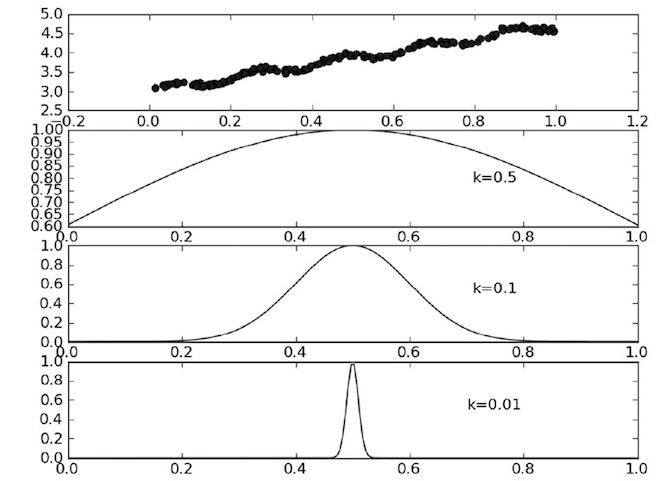
- 基于上图我们能发现两个规律:
- 假定我们正预测的点是 x=0.5,一定要记住 x 的对应值不再是一个数值,它的对应值变成了向量,所以这是 x=0.5后的新图像,牢记它变成了一个向量,最上面的是原始数据集;第二个图显示了当 k=0.5 时,大部分数据都用于训练回归模型;最下面的图显示当 k=0.01 时,仅有很少的局部点被用于训练回归模型。
- 如果(|x^{(i)}-x|approx0),则(w_{(i)}approx1);如果(|x^{(i)}-x|approxinfty),则(w^{(i)}approx0)
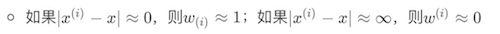
重点来了,我刚开始不明白的就是这里,上面 两个注意+图片解释 其实已经揭晓了答案
离 x 很近的样本,权值接近1;而离 x 很远的样本,此时权值接近于0,这样就在 x 局部构成线性回归,x 构成的线性回归依赖的事 x 周边的点,而不类似于线性回归依赖训练集中的所有数据。
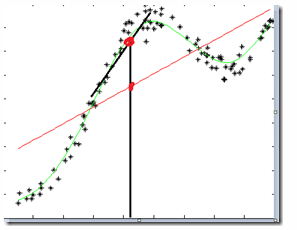
上图红线是某个点 x 基于训练集中所有数据使用线性回归做的结果,黑色直线使用 LWLR 做的结果,由于在每个数据都会重复局部加权的过程,并且不断地每个点的回归系数也在不断的改变,因此它会很好的拟合数据集,进而消除了线性回归拟合不好的缺点。(有点类似极限或者求导或者微积分的思想,总之就是把一个大的物体切割成一大部分,然后对于每一部分进行计算)。
说到了LWLR的优点,不得不说说它的缺点,上一段讲到了训练集中的每个数据都会重复局部加权的过程,因此他的计算量是庞大的,并且他的回归系数是基于周围的数据计算出来的,因此下次需要预测某个数据的分类时,需要再一次输入所有的数据。即线性回归算法是参数学习算法,一旦拟合出合适的回归系数,对于之后的预测,不需要再使用原始训练数据集;局部加权线性回归算法是非参数学习算法,每次进行预测都需要全部的训练数据,无法算出固定的回归系数。
最后看一看 线性回归和不同 k 值的局部加权线性回归 对相同数据集的结果。
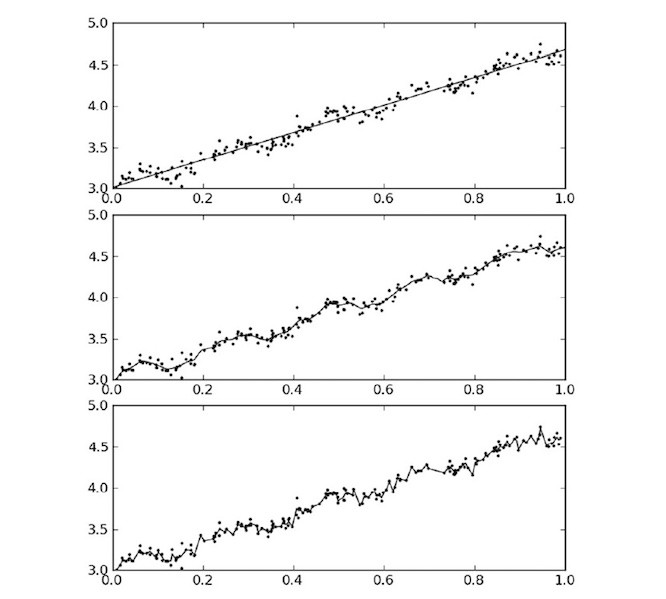
上图第一张图使用的是 k=1 的LWLR(类似于线性回归),第二张图使用的是 k=0.01 的LWLR,第三张图使用的 k=0.003 的 LWLR。第一张图明显欠拟合,第二张图很合适,第三张图过拟合。