银行风险控制模型[二分类]
目录
1 数据读取与变量划分
1.1 读取数据
import pandas as pd
inputfile = './bankloan.xls'
data = pd.read_excel(inputfile)
通过data.head()查看前五行数据,结果如下:
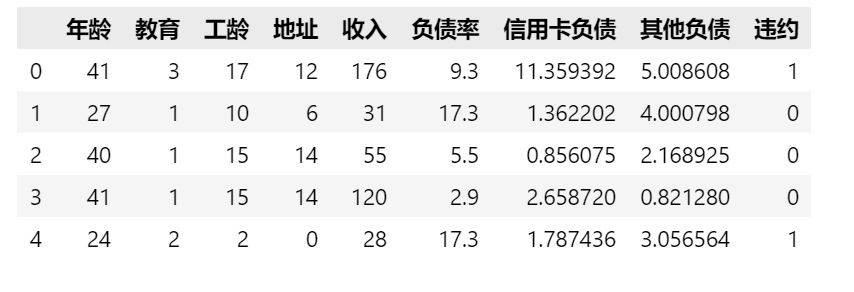
该数据集共700条记录;最后一列表示负债与否, ‘0’表示未违约,‘1’表示违约。
1.2 划分特征变量与目标变量
X = data.drop(columns='违约')
y = data['违约']
2 逻辑回归模型~sklearn
2.1 模型的搭建与使用
- 训练模型
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
model = LogisticRegression()
model.fit(X_train, y_train)
- 预测数据结果
y_pred = model.predict(X_test)
打印y_pred查看预测值

可以将预测值与真实值放在一起对比一下,结果如下表(展示前五项):
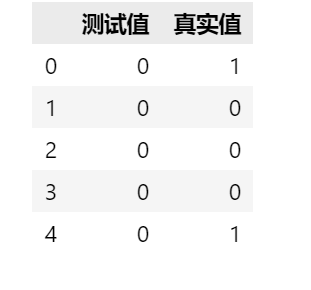
2.2 准确率与混淆矩阵
from sklearn.metrics import accuracy_score
score = accuracy_score(y_pred, y_test)
print(score)
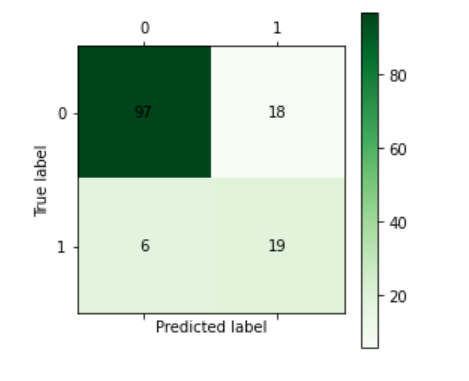
使用accuracy_score函数,score的结果为0.8285714285714286,即准确度为82.8%。
- 接下来画出混淆矩阵
- 先写入混淆矩阵可视化函数
def cm_plot(y, y_pred):
from sklearn.metrics import confusion_matrix #导入混淆矩阵函数
cm = confusion_matrix(y, y_pred) #混淆矩阵
import matplotlib.pyplot as plt #导入作图库
plt.matshow(cm, cmap=plt.cm.Greens) #画混淆矩阵图,配色风格使用cm.Greens,更多风格请参考官网。
plt.colorbar() #颜色标签
for x in range(len(cm)): #数据标签
for y in range(len(cm)):
plt.annotate(cm[x,y], xy=(x, y), horizontalalignment='center', verticalalignment='center')
plt.ylabel('True label') #坐标轴标签
plt.xlabel('Predicted label') #坐标轴标签
return plt
- 传入参数
cm_plot(y_test, y_pred)
3 BP神经网络~Keras
3.1 模型的搭建与使用
- 训练模型
from keras.models import Sequential
from keras.layers.core import Dense, Activation
from keras.layers import Activation, Dense, Dropout
model = Sequential()
model.add(Dense(64,input_dim=8,activation='relu')) #8个特征维度
# Drop防止过拟合的数据处理方式
model.add(Dropout(0.5))
model.add(Dense(64,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(1,activation='sigmoid'))
# 编译模型,定义损失函数,优化函数,绩效评估函数
model.compile(loss='binary_crossentropy',
optimizer='rmsprop',
metrics=['accuracy']) #二元分类,所以指定损失函数为binary_crossentropy
# 导入数据进行训练
model.fit(X_train,y_train,epochs=200,batch_size=128)
- 预测数据结果
yp = model.predict_classes(X_test).reshape(len(y_test)) # 分类预测
print(yp)

3.2 准确率与混淆矩阵
score = model.evaluate(X_test,y_test,batch_size=128)
print(score)
得到当前模型的损失值为0.38988085644585746,精度为0.8285714387893677。当然适当提高迭代次数,可提高精确度。
- 依然使用上面的混淆矩阵可视化函数,传入对应参数yp
cm_plot(y_test, yp)
相应的混淆矩阵结果如下图:
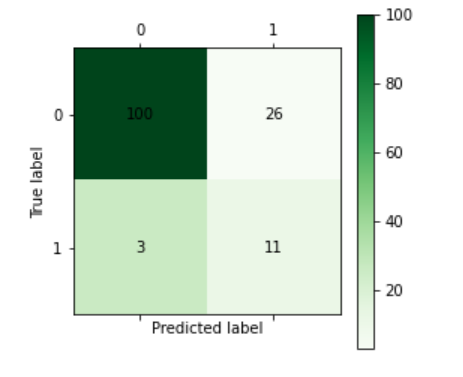
对比: 从准确率来看,两个模型的差别不大;从混淆矩阵来看,神经网络模型略胜一筹。总的来说,两个模型对此数据集的预测结果均为良好,不存在大的差别。