激活函数

tanh(z) =  (e^z - e^-z ) / ( e^z + e^-z )

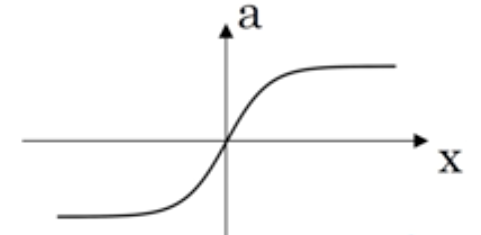
tanh函数几乎在所有场合都更优越

用σ激活函数的一个例外场合是：使用二元分类的时候。因为二元分类问题概率数值应在（0，1）之间

 因此可以在隐藏层用tanh函数，在输出层y帽计算时用σ函数

现在σ函数和tanh函数都有一个缺点就是，如果z非常大或者非常小，那么导数的梯度或者说这个函数的斜率可能就很小，函数的斜率很接近0，这样会拖慢梯度下降算法

这时候会用到ReLU函数

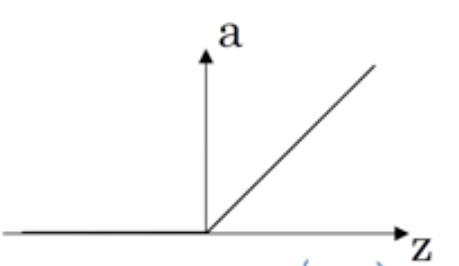
 只要z为正，导数就是1，当z为负时，斜率为0

在选择激活函数时有一些经验法则：

如果你的输出值是0和1，如果你在做二元分类，那么σ函数很适合作为输出层的激活函数。然后其他所有单元都用ReLU（所谓的线性修正单元），现在已经编程激活函数的默认选择了

若果不确定隐藏层用哪个，我们就用ReLU作为激活函数，这是今天大多数人都在用的，虽然有时也会用tanh激活函数

而ReLU的一个缺点就是，当z为负时，导数等于0，在实践中没有任何问题，但是ReLU还有另一个版本叫做带泄露的ReLU，当z为负时，函数不再为0，它有一个很平缓的斜率，不过是集中使用频率没有那么高

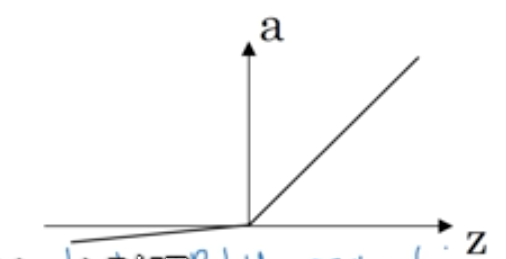
                                          ReLU    a = max ( 0.01z , z )

在激活函数中用ReLU，神经网络学习的速度通常会快很多，比使用tanh和σ激活函数快得多