重建二叉树结构,给定了前序和中序,重建树形结构
#include <iostream> #include <string> using namespace std; /* 给定前序,中序,重建树结构 例如假定: 前序:adbcef 中序:dbaecf 后序:dbefca */ struct NODE{ NODE *pLeft; NODE *pRight; char chValue; }; //递归构建树 NODE* Rebuild(char *pPreOrderStart,char* pPreOrderEnd,char* pInOrderStart,char *pInOrderEnd) { NODE *root = (NODE*)malloc(sizeof(NODE)); root->chValue = pPreOrderStart[0]; root->pLeft = root->pRight = NULL; //如果只剩下最后一个节点返回他 if (pPreOrderStart == pPreOrderEnd && pInOrderStart == pInOrderEnd) { return root; } char* rootInOrder = pInOrderStart; while(rootInOrder != pInOrderEnd && *rootInOrder != root->chValue)rootInOrder++; if(rootInOrder == pInOrderEnd && root->chValue != root->chValue)return NULL; int leftLen = rootInOrder - pInOrderStart; char* leftPreOrderEnd = pPreOrderStart+leftLen; if (leftLen > 0) { root->pLeft = Rebuild(pPreOrderStart+1,leftPreOrderEnd,pInOrderStart,rootInOrder-1); } if (leftLen < pPreOrderEnd - pPreOrderStart) { root->pRight = Rebuild(leftPreOrderEnd+1,pPreOrderEnd,rootInOrder+1,pInOrderEnd); } return root; } //重建树 void RebuildTree(char *pPreOrder,char *pInOrder,int nTreeLen,NODE** pRoot) { if(nTreeLen == 0 || pPreOrder == NULL || pInOrder == NULL)return; //构建树 *pRoot = Rebuild(pPreOrder,pPreOrder+nTreeLen-1,pInOrder,pInOrder+nTreeLen-1); } //先根遍历 void preRootView(NODE* root) { cout<<root->chValue; if (root->pLeft != NULL ) { preRootView(root->pLeft); } if (root->pRight != NULL ) { preRootView(root->pRight); } } //中根遍历 void inRootView(NODE* root) { if (root->pLeft != NULL ) { inRootView(root->pLeft); } cout<<root->chValue; if (root->pRight != NULL ) { inRootView(root->pRight); } } //后根遍历 void afRootView(NODE* root) { if (root->pLeft != NULL ) { afRootView(root->pLeft); } if (root->pRight != NULL ) { afRootView(root->pRight); } cout<<root->chValue; } int main(int argc, char **argv) { char *preOrder = "abdcef"; char *inOrder = "dbaecf"; NODE *pRoot = (NODE*)malloc(sizeof(NODE)); int len = strlen(preOrder); pRoot->chValue = *preOrder; RebuildTree(preOrder,inOrder,len,&pRoot); cout<<"先根遍历:"; preRootView(pRoot); cout<<endl; cout<<"中根遍历:"; inRootView(pRoot); cout<<endl; cout<<"后根遍历:"; afRootView(pRoot); cout<<endl; return 0; }
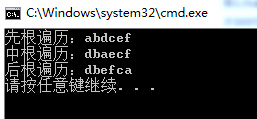
运行结果: