8皇后以及N皇后算法探究，回溯算法的JAVA实现，非递归，循环控制及其优化

上两篇博客

8皇后以及N皇后算法探究，回溯算法的JAVA实现，递归方案

8皇后以及N皇后算法探究，回溯算法的JAVA实现，非递归，数据结构“栈”实现

研究了递归方法实现回溯，解决N皇后问题，下面我们来探讨一下非递归方案

实验结果令人还是有些失望，原来非递归方案的性能并不比递归方案性能高

代码如下：

package com.newflypig.eightqueen;

import java.util.Date;

/**
 * 使用循环控制来实现回溯，解决N皇后
 * @author newflydd@189.cn
 * Time : 2016年1月1日 下午9:37:32
 */
public class EightQueen4 {
    private static short K=15;
    private static short N=0;
    private static boolean dead=false;    //下方走到了死路
    
    public static void main(String[] args) {
        for (N = 9; N <= K; N++) {
            
            Date begin = new Date();
            
            dead=false;
            long count = 0;

            /**
             * -2：初始状态，尚未摆放 -1：开始尝试摆放 0到N-1：皇后安全的摆放在这一列的哪一行
             */
            short[] chess = new short[N];
            for (short i = 1; i < N; i++)
                chess[i] = -2;
            OUT: while (chess[0] != -2) {
                if (dead) {

                    /**
                     * 如果下方的皇后已经摆无可摆，已经走到死路 则要将当前最后一个安全的皇后右移 右移成功后，判断安全性
                     * 安全：dead清除，继续外部循环 不安全，则继续右移，直至边界溢出，再次死路
                     */
                    while (moveStep(chess)) {
                        if (isSafety(chess)) {
                            dead = false;
                            continue OUT;
                        }
                    }

                } else {
                    /**
                     * 如果当前状态下的安全棋盘并没有接受到下方传来的死路信号 则需要进一步探测下一行的摆放位置
                     */
                    short row = getRow(chess);
                    chess[row + 1] = -1; // 准备对下一层摆放皇后

                    while (moveStep(chess)) {
                        if (isSafety(chess)) {
                            if (row + 1 == N - 1) { // 如果最后一行找到了一个可能解
                                count++; // 计数+1

                                /**
                                 * 找到解以后，dead设为死路，最后一行清掉皇后，同时倒数第二行也要清掉皇后
                                 */
                                dead = true;
                                chess[N - 1] = -2;

                                continue OUT;
                            }
                            continue OUT;
                        }
                    }
                }
            }

            Date end = new Date();
            System.out.println("解决 " + N + "皇后问题，用时：" + String.valueOf(end.getTime() - begin.getTime()) + "毫秒，计算结果："
                    + count);
        }
    }


    private static boolean moveStep(short[] chess) {
        short row=getRow(chess);
        if(chess[row]+1>=N){
            /**
             * 摆到边界，清空当前行的摆放记录，标志死路
             */            
            chess[row]=-2;
            dead=true;            
            return false;        
        }
        chess[row]=(short) (chess[row]+1);
        return true;
    }


    private static short getRow(short[] chess) {
        short row=(short) (N-1);
        while(chess[row]==-2){
            row--;
        }
            
        return row;
    }
    
    private static boolean isSafety(short[] chess) {
        short row=getRow(chess);
        short col=chess[row];
        
        //判断中上、左上、右上是否安全
        short step=1;
        for(short i=(short) (row-1);i>=0;i--){
            if(chess[i]==col)    //中上
                return false;
            if(chess[i]==col-step)    //左上
                return false;
            if(chess[i]==col+step)    //右上
                return false;
            
            step++;
        }
        
        return true;
    }
}

程序中定义了全局变量dead死路标志，告诉循环什么时候需要回溯，什么时候需要继续深搜

getRow() 函数返回当前最后摆放皇后的行号，每次摆放皇后和判断安全性时都要调用，所以显得性能偏低

下面取消了getRow()函数，使用全局变量row来表示已经摆到那一行的皇后了，用一个小小的变量空间换了一部分时间：

package com.newflypig.eightqueen;

import java.util.Date;

/**
 * 使用循环控制来实现回溯，解决N皇后
 * 开辟两个变量控制行和列，避免不必要的计算，空间换时间
 * @author newflydd@189.cn
 * Time : 2016年1月1日 下午9:37:32
 */
public class EightQueen5 {
    private static short K=15;
    private static short N=0;
    private static boolean dead=false;    //下方走到了死路
    private static short row=0;
    
    public static void main(String[] args) {
        for (N = 9; N <= K; N++) {
            
            Date begin = new Date();
            
            row=0;
            dead=false;
            long count = 0;
            /**
             * -2：初始状态，尚未摆放 -1：开始尝试摆放 0到N-1：皇后安全的摆放在这一列的哪一行
             */
            short[] chess = new short[N];
            for (short i = 1; i < N; i++)
                chess[i] = -2;
            OUT: while (chess[0] != -2) {
                if (dead) {

                    /**
                     * 如果下方的皇后已经摆无可摆，已经走到死路 则要将当前最后一个安全的皇后右移 右移成功后，判断安全性
                     * 安全：dead清除，继续外部循环 不安全，则继续右移，直至边界溢出，再次死路
                     */
                    while (moveStep(chess)) {
                        if (isSafety(chess)) {
                            dead = false;
                            continue OUT;
                        }
                    }

                } else {
                    /**
                     * 如果当前状态下的安全棋盘并没有接受到下方传来的死路信号 则需要进一步探测下一行的摆放位置
                     */
                    chess[++row] = -1; // 准备对下一层摆放皇后

                    while (moveStep(chess)) {
                        if (isSafety(chess)) {
                            if (row  == N - 1) { // 如果最后一行找到了一个可能解
                                count++; // 计数+1

                                /**
                                 * 找到解以后，dead设为死路，最后一行清掉皇后
                                 */
                                dead = true;
                                chess[N - 1] = -2;
                                row--;

                                continue OUT;
                            }
                            continue OUT;
                        }
                    }
                }
            }

            Date end = new Date();
            System.out.println("解决 " + N + "皇后问题，用时：" + String.valueOf(end.getTime() - begin.getTime()) + "毫秒，计算结果："
                    + count);
        }
    }


    private static boolean moveStep(short[] chess) {
        if(chess[row]+1>=N){
            /**
             * 摆到边界，清空当前行的摆放记录，标志死路
             */            
            chess[row]=-2;
            row--;
            dead=true;            
            return false;        
        }
        chess[row]=(short) (chess[row]+1);
        return true;
    }
    
    private static boolean isSafety(short[] chess) {
        short col=chess[row];
        
        //判断中上、左上、右上是否安全
        short step=1;
        for(short i=(short) (row-1);i>=0;i--){
            if(chess[i]==col)    //中上
                return false;
            if(chess[i]==col-step)    //左上
                return false;
            if(chess[i]==col+step)    //右上
                return false;
            
            step++;
        }
        
        return true;
    }
}

最终的执行效率为：

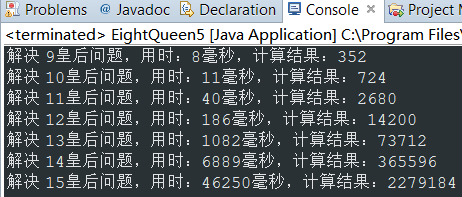
这跟我们第一篇博客的递归调用的效率：

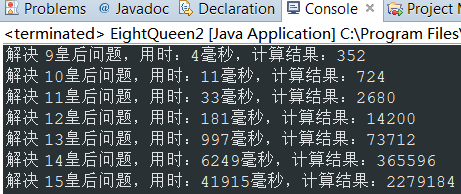
还是有些差距，所以算法届大张旗鼓的所谓“递归影响性能”的说法并不存在，至少在这个问题上有待探讨

最后我还想再实现以下多线程解决N皇后的问题

因为我发现无论用不用递归，我的N皇后程序跑起来的时候，CPU使用率都在15%以下

可能用了JAVA的缘故，虚拟机沙盒有限制，而且是多核的CPU，暂时也没搞明白为什么不能发挥更高的CPU使用率

最后我将用多线程再次尝试更高的程序性能，看看能否有突破。