[BZOJ 2007] 海拔

Link:https://www.lydsy.com/JudgeOnline/problem.php?id=2007

Algorithm:

由于起点高度为0，终点高度为1，明显没有必要有比1大的点

因此得到结论：原图仅由0和1构成，且0和1不交错排布

那么所有对答案的贡献都来自于0和1的分界线，那么就将问题转化为求最小割

但点数过多，网络流明显会超时，那么此时就要用到对偶图了

如果一个图是平面图（无边的相交），则可以将面化为点，构建对偶图，如下图所示

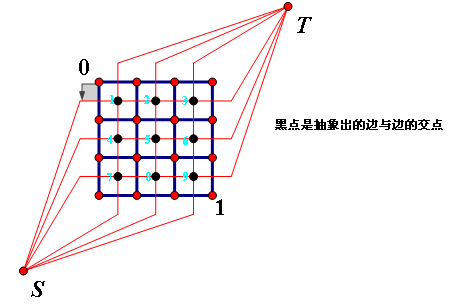
这样就能把求平面图的最小割问题  -------->  求其对偶图的ST最短路   妙啊

由于此题为有向图，每条边的从S到T还是从T到S的性质不能改变

因此原左右、上下边现在由S到T，而右左、下上由T到S

Code:

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef pair<int,int> P;

const int MAXN=500+10;
int num[MAXN][MAXN],n,s,t;
vector<P> G[MAXN*MAXN];

ll dist[MAXN*MAXN];
queue<int> que;

inline int read()
{
    char ch;int num,f=0;
    while(!isdigit(ch=getchar())) f|=(ch=='-');
    num=ch-'0';
    while(isdigit(ch=getchar())) num=num*10+ch-'0';
    return f?-num:num;
}

void add_edge(int x,int y,int val)
{
    G[x].push_back(P(y,val));
}

int main()
{
    n=read();s=0;t=n*n+1;  //预处理每个点在对偶图中的编号
    for(int i=1;i<=n;i++)
        num[0][i]=num[i][n+1]=s,num[i][0]=num[n+1][i]=t;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            num[i][j]=(i-1)*n+j;
    
    int x;    
    for(int i=0;i<=n;i++)  //构图
        for(int j=1;j<=n;j++)
            x=read(),add_edge(num[i][j],num[i+1][j],x);
    for(int i=1;i<=n;i++)
        for(int j=0;j<=n;j++)
            x=read(),add_edge(num[i][j+1],num[i][j],x);
    for(int i=0;i<=n;i++)
        for(int j=1;j<=n;j++)
            x=read(),add_edge(num[i+1][j],num[i][j],x);
    for(int i=1;i<=n;i++)
        for(int j=0;j<=n;j++)
            x=read(),add_edge(num[i][j],num[i][j+1],x);
    
    memset(dist,0x3f,sizeof(dist));  //SPFA求最短路
    que.push(s);dist[s]=0;
    while(!que.empty())
    {
        int u=que.front();que.pop();
        for(int i=0;i<G[u].size();i++)
        {
            P t=G[u][i];int v=t.first;
            if(dist[v]>dist[u]+t.second)
                dist[v]=dist[u]+t.second,que.push(v);
        }
    }
    cout << dist[t];
    return 0;
}

1、熟悉平面图  到   对偶图的转换

2、最小割问题可以在对偶图中用最短路算法解决

3、对偶图建图

预处理出每个点的编号，将最外层（0、N+1）留给S和T

要确定每条边是从S到T还是T到S的性质不改变