定义:
有序二叉树
任何节点的左右子树高度差不超过1
平衡因子BF(rightTreeDeep - leftTreeDeep)
查询时间复杂度稳定: log2N
旋转
当插入新节点时触发当前节点平衡因子计算,以及回溯计算父节点平衡因子(bf),当发现存在节点 |bf| >= 2时,触发旋转
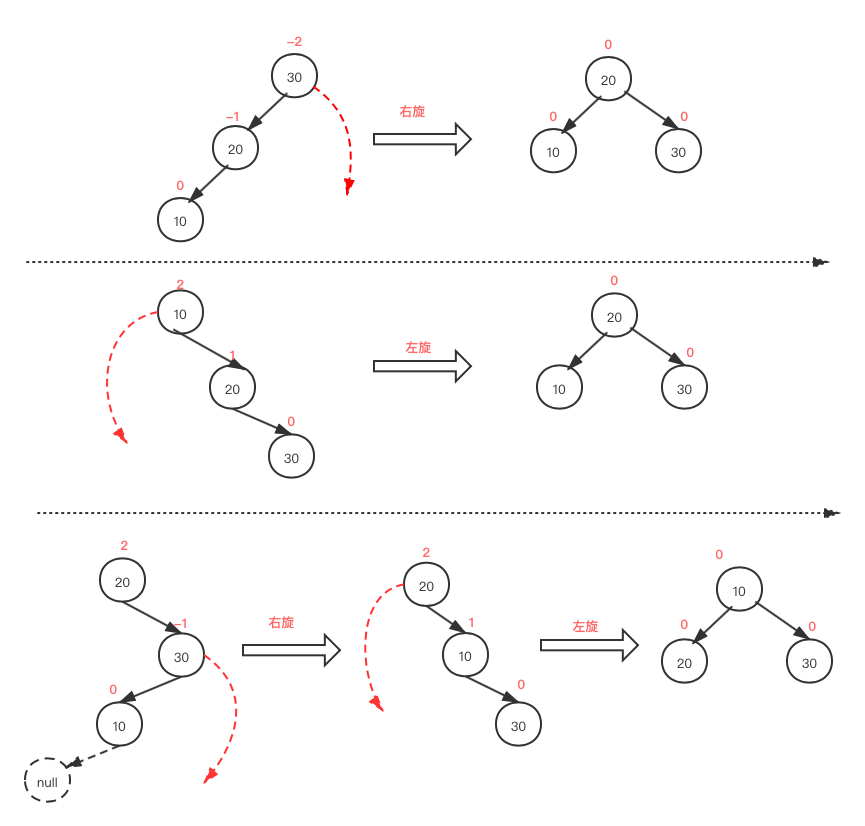
四种情况:
2, 1, 0 左旋
-2, -1, 0 右旋
2, -1, 0 先右旋再左旋
-2, 1, 0 先左旋再右旋
需要两次旋转组合的原因: 简单的左旋或者右旋无法满足二叉树的左比右小的基本要素
代码实现
节点实现(核心)
public class AvlTreeNode { int value; int bf; AvlTreeNode leftChild; AvlTreeNode rightChild; public AvlTreeNode(int value) { this.value = value; bf = 0; } /** * 添加子节点 * @param subNode */ public void addNode(AvlTreeNode subNode) { if(subNode.value <= this.value) { // 在左子树上添加新节点 if(leftChild == null) { leftChild = subNode; } else { leftChild.addNode(subNode); } } else { // 在右子树上添加新节点 if(rightChild == null) { rightChild = subNode; } else { rightChild.addNode(subNode); } } // 平衡因子 > 1 则触发旋转 if(Math.abs(calBf()) > 1) { rotate(); } } /** * 计算节点平衡因子(右子树高 - 左子树高) * @return */ public int calBf() { int leftDeep = 0; int rightDeep = 0; if(null != leftChild) { leftDeep = leftChild.getSubDeep(); } if(null != rightChild) { rightDeep = rightChild.getSubDeep(); } this.bf = rightDeep - leftDeep; return this.bf; } public void rotate() { if (-2 == this.bf) { if(-1 == leftChild.calBf()) { // 直接右旋 rightRotate(); } else { // 先左旋 leftChild.leftRotate(); // 再右旋 rightRotate(); } } else if (2 == this.bf) { if(1 == rightChild.calBf()) { // 直接右旋 leftRotate(); } else { // 先左旋 rightChild.rightRotate(); // 再右旋 leftRotate(); } } } /** * 右旋 */ public void rightRotate() { // 克隆当前节点(顶节点)后面右旋, 当前节点降级为中间节点 AvlTreeNode tmpNode = new AvlTreeNode(this.value); // 废弃中间节点, 当前节点替换原中间节点 value = leftChild.value; // 将原中间节点的原右子树嫁接到右旋节点的左子树上 tmpNode.leftChild = leftChild.rightChild; // 右旋节点的左子树保持不变 tmpNode.rightChild = rightChild; // 将原中间节点的左子树嫁接到当前顶节点的左子树 leftChild = leftChild.leftChild; // 右旋顶端节点 rightChild = tmpNode; } /** * 左旋 */ public void leftRotate() { // 克隆当前节点(顶节点)后面右旋, 当前节点降级为中间节点 AvlTreeNode tmpNode = new AvlTreeNode(this.value); // 废弃原中间节点, 当前节点替换中间节点 value = rightChild.value; // 将原中间节点的左子树调整到左旋节点的右子树上 tmpNode.rightChild = rightChild.leftChild; // 左旋节点的左子树保持不变 tmpNode.leftChild = leftChild; // 将原中间节点的右子树嫁接到当前顶节点的左子树 rightChild = rightChild.rightChild; // 左旋顶端节点 leftChild = tmpNode; } /** * 获取子树深度 * @return */ public int getSubDeep() { int leftDeep = 0; int rightDeep = 0; if(leftChild != null) { leftDeep = leftChild.getSubDeep(); } if(rightChild != null) { rightDeep = rightChild.getSubDeep(); } int subDeep = leftDeep >= rightDeep ? leftDeep : rightDeep; return subDeep + 1; } /** * 前序遍历 */ public void print() { if(leftChild != null) { leftChild.print(); } System.out.println("value: " + value + " bf: " + calBf()); if(rightChild != null) { rightChild.print(); } } }
树实现
public class AvlTree { AvlTreeNode rootNode = null; public void addNode(AvlTreeNode node) { if(null == rootNode) { rootNode = node; return; } rootNode.addNode(node); } /** * 前序遍历 */ public void print() { rootNode.print(); } }
测试类
public class TreeTest { public static void main(String[] args) { AvlTree tree = new AvlTree(); // 先左旋 后右旋 tree.addNode(new AvlTreeNode(20)); tree.addNode(new AvlTreeNode(10)); tree.addNode(new AvlTreeNode(5)); tree.addNode(new AvlTreeNode(30)); tree.addNode(new AvlTreeNode(40)); tree.addNode(new AvlTreeNode(25)); tree.print(); } }