快速入门Numpy

教你十分钟学会使用numpy。
简单介绍一下numpy的话，这就是一个基于多维数组的python科学计算的核心库。

基本信息

# 一般用np作为numpy的缩写
import numpy as np

# 这里创建了一个数组 之后详细说明
arr = np.array([[[1], [2]], [[3], [4]]], dtype=np.int32)

# 数组的维度
arr.ndim

# 数组的各个维度的长度
arr.shape

# 数组元素个数
arr.size

索引对象

这里要说一个贯穿数据索引的重要概念。无论是原生的python list容器，numpy，还是之后的pandas都会用到。
在原生的python list容器中我们一般会用list[start:end:step]做列表索引，那么我们用于索引的对象就是start:end:step即切片对象(slice)。
numpy扩展了可以用于索引的对象。我们可以用任意的序列对象作为索引。比如在numpy中array[1:4]和array[[1,2,3]]是等效的。但是在list容器的索引语法中，后面这种写法是非法的。

多维视图

那么上面是单个维度的索引，多维索引只要把单维的堆叠起来就行就行了。
比如arr[first_slice, second_slice, ......]。

结合下面的例子来理解一下。

注意所以视图的返回都是引用。
但也可也通过这种方式来返回拷贝，newarr = arr[::].copy()。

快速创建

我们可以用任意指定的shape来创建多维数组。shape即元组或者列表比如(3,4)就是一个3x4矩阵， [2,3,4] 就是一个2x3x4的三维张量。

# 创建一个全为1的多维数组
np.ones(shape)

# 创建一个全为0的多维数组
np.zeros(shape)

# 创建一个全为7的多维数组
np.full(shape,7)

# 创建一个随机的数组
np.random.random(shape)

# n阶单位方阵即二维多维数组
np.eye(n)

# 二维数组即矩阵对角线填充
np.diag([1, 2, 3])

数组操作

# 运算操作，以加操作为例
result = a - b
result = np.add(a,b) # 跟操作符等效

# 函数操作
np.exp(arr)  # e的次数
np.sqrt(arr) # 平方根
np.log(arr)  # 对数
a.dot(b)     # a点积b
a.T          # a的转置

# 比较操作
a == b # 会返回一个由True和False构成的多维数组

# 聚合操作
arr.sum()    # 求和
arr.mean()   # 求均值
a.corrcoef() # 求协方差

这里有一个容易弄混在于聚合操作，arr.sum()默认是对所有的元素进行求和操作。但是其实我们还可以指定arr.sum(axis=0)对某个维度进行求和。
这里以三维张量举个例子：

>>> arr = np.ones((2,3,4))
>>> arr
array([[[ 1.,  1.,  1.,  1.],
        [ 1.,  1.,  1.,  1.],
        [ 1.,  1.,  1.,  1.]],

       [[ 1.,  1.,  1.,  1.],
        [ 1.,  1.,  1.,  1.],
        [ 1.,  1.,  1.,  1.]]])
>>> arr.sum(axis=0)
array([[ 2.,  2.,  2.,  2.],
       [ 2.,  2.,  2.,  2.],
       [ 2.,  2.,  2.,  2.]])
>>> arr.sum(axis=1)
array([[ 3.,  3.,  3.,  3.],
       [ 3.,  3.,  3.,  3.]])
>>> arr.sum(axis=2)
array([[ 4.,  4.,  4.],
       [ 4.,  4.,  4.]])

简单来理解的话，对某个axis=n进行聚合操作的话就是把对应shape的第n个维度消去。
比如原本的shape为(2,3,4)，如果指定axis=0，那么聚合操作的返回shape就是(3,4)。可以结合上面那个例子来理解。

速查表

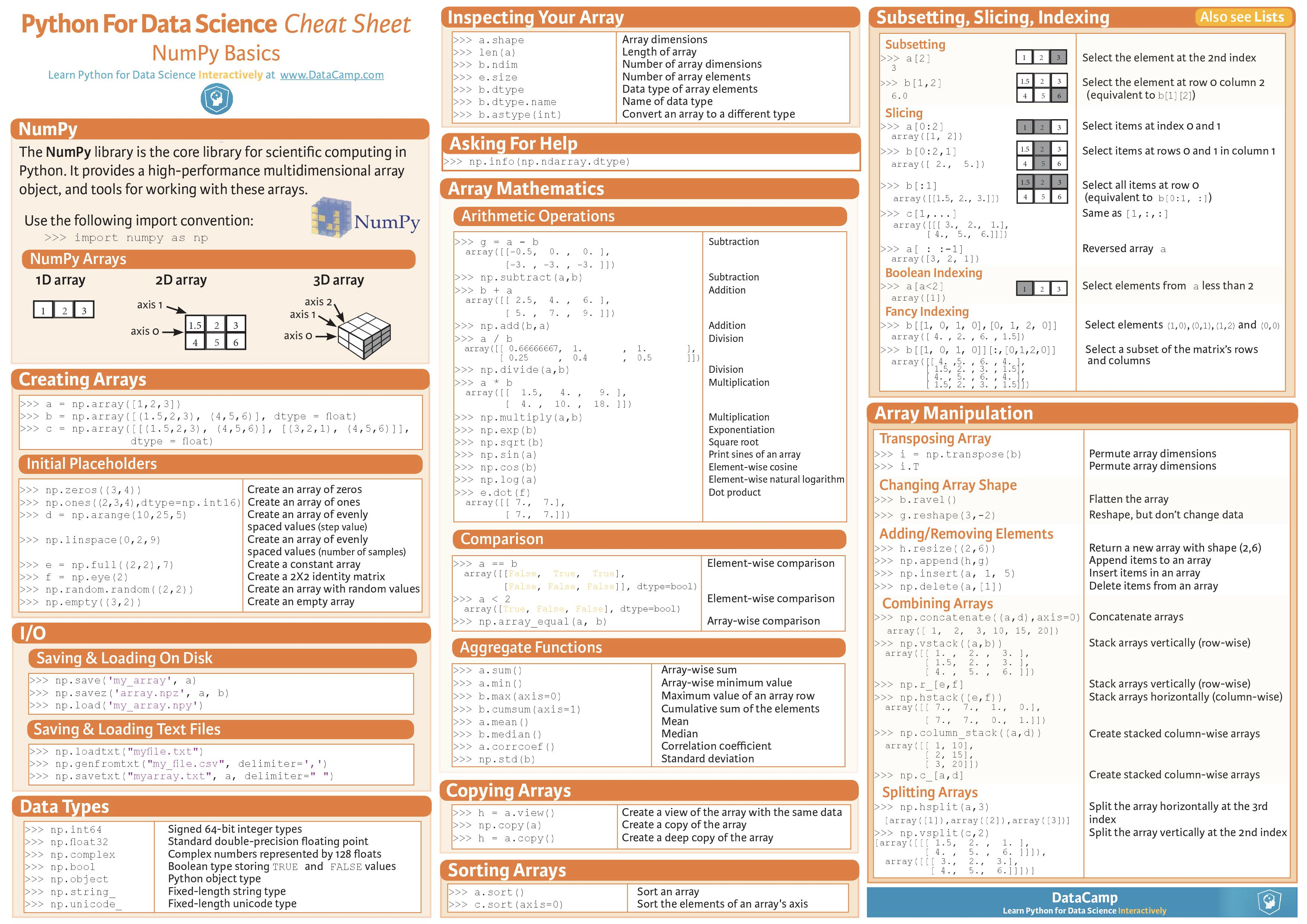
练习

你以为你十分钟真的就学会了吗。
来做点习题吧。
100道numpy练习题

参考

scpy-note numpy