算法思想之动态规划

动态规划一直被认为是最难理解的一种算法思想，什么重叠子问题、动态转移方程、最优子结构等等，一听就高深莫测，没有往下学习下去的动力

一、初识动态规划

废话不多说，我们直接先上一个经典的例子。那就是耳熟能详的斐波那契数列问题。我们先来看一下问题的定义。

斐波那契数列的定义如下：    斐波那契数列指的是这样一个数列 0,1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,.....   它以递归的方法来定义： F(0)=0，F(1)=1, F(n)=F(n-1)+F(n-2)（n>=2，n∈N*）

1. 递归解决：

     这个例子最直观的方法就是用递归的方式来实现，毕竟斐波那契数列是用递归来定义的。我们来看一下代码实现。

def fibs(n):
     if n<2:
          return n
     return fibs(n-1)+fibs(n-2)

C#实现

public static int Foo(int i)
        {
            if (i <= 0)
            {
                return 0;
            }
            else if (i > 0 && i <= 2)
            {
                return 1;
            }
            else
            {
                return Foo(i - 1) + Foo(i - 2);
            }
        }

这样是不是很简单。我们接下来看一下调用的递归树。我们以fibs(6)为例。

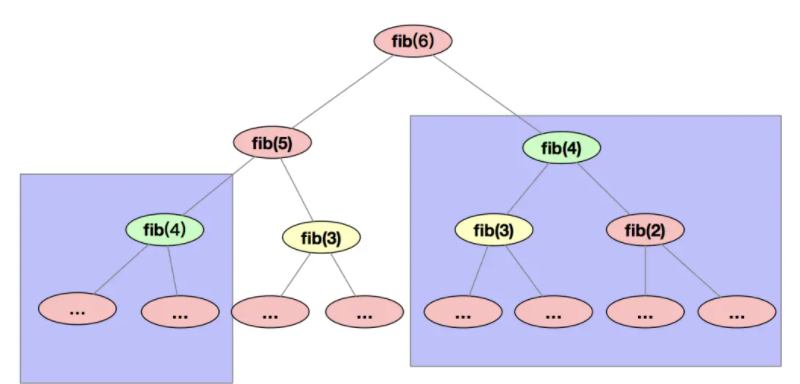
 其中每个结点表示要计算的斐波那契数列的第几项，我们可以从上图发现，会出现许多重复计算的问题，比如fib(4)就计算了两次。这样就会带来时间和空间上的消耗，那我们有什么方式可以避免重复计算的问题。我们可以使用递归中的“备忘录”功能来解决。我们来看一下代码如何实现。

二、用动态规划解决

我们把整个求解过程分为n个阶段，每个阶段去求解数列对应项的值。我们在解决当前问题时，也就是求解该对应项的值的时候，会依赖过去的状态，也就是前面几项的值来计算。比如我们在求解fibs(6)的时候，我们需要用到fibs(5)和fibs(4)这两项。 我们来定义一个数组，来记录每项的状态。我们也叫做状态转移矩阵。 按照斐波那契数列的定义：

F(0)=0,F(1)=1
F(n)=F(n-1)+F(n-2) (n>=2)

我们可以看到F(n)的值只与他的前两个状态有关。所以我们只要知道他的前两个状态，就可以求出F(n)。

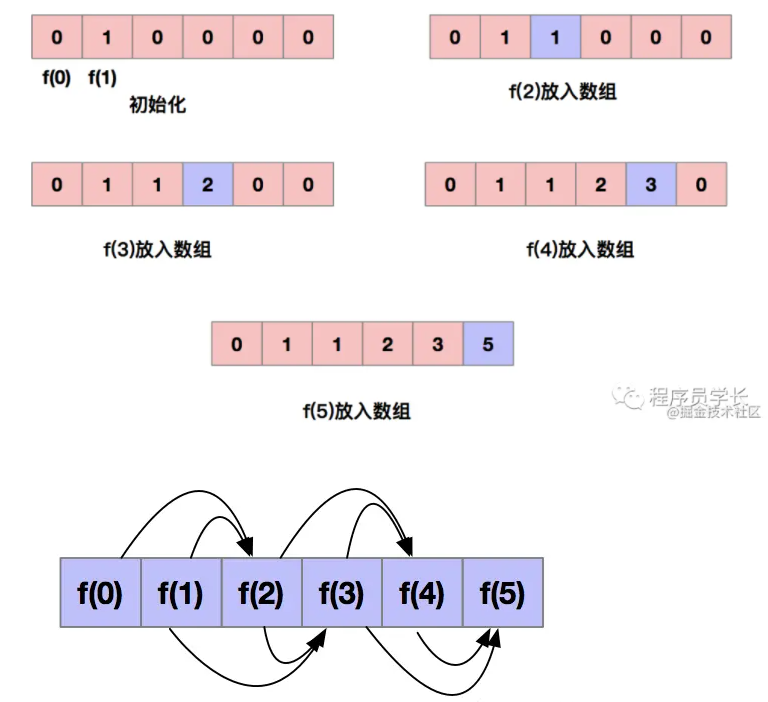
1. 初始化值F(0)=0，F(1)=1，我们直接放入数组中。
2. 要想计算F(2)，我们需要知道F(0)和F(1)，因为上一步已经放入数组中，我们直接拿来用就好了，然后把F(2)的结果放入数组中。
3. 要想计算F(3)，我们需要知道F(2)和F(1)，因为F(2)和F(1)已经存在数组里了，我们直接拿来用就好了，然后把F(3)的结果放入数组中。

    ....

 依此类推，知道计算到n为止。整个状态转移矩阵就计算好了。如下图所示。我们以求解F(5)为例。

 下面我们直接看代码实现，这样比较简单明了。

def fibs(n):
     if n<2:
          return n
     dp=[0 for _ in range(n+1)]
     dp[0]=0
     dp[1]=1
     for i in range(2,n+1):
          dp[i]=dp[i-1]+dp[i-2]
     return dp[n]
print(fibs(6))

上面的代码是不是很简洁明了。这就是一种用动态规划来解决问题的思路。我们把问题分解为n个阶段，一个阶段一个阶段去求解。然后通过当前状态，来求出下一个状态，动态的往前推进，这是不是还挺形象的