牛客网每日一练

#
# 
# @param m int整型 
# @param n int整型 
# @return int整型
#
class Solution:
    def uniquePaths(self , m , n ):
        dp = [[1 for i in range(n)] for j in range(m)]
        for i in range(1,m):
            for j in range(1,n):
                dp[i][j] = dp[i-1][j] + dp[i][j-1]
        return dp[m-1][n-1]
        # write code here

一个机器人在m×n大小的地图的左上角（起点）。
机器人每次向下或向右移动。机器人要到达地图的右下角（终点）。
可以有多少种不同的路径从起点走到终点？

题解：这是一个非常典型的Dynamic Programming问题，首先我们可以发现第一行和第一列只有一种方法可以达到

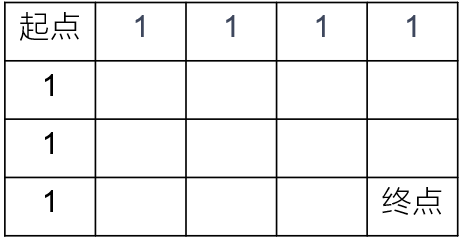
 对于其它位置来说，到达这个位置有两种情况：
一种是从上面的格子走过来的
另一种是从左边的格子走过来的

 所以，我们定义一个×大小的二维数组
[][]表示从起点到达第行第列的方案数。
先把第一行第一列赋值为1
然后从第二行第二列的元素开始循环
[][]=[−1][]+[][−1]
右下角的dp值就是我们要求的答案