bzoj 3944 杜教筛

题目中要求phi和miu的前缀和，利用杜教筛可以推出公式。我们令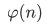为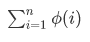

那么有公式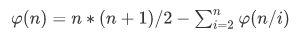

类比欧拉函数，我们可以推出莫比乌斯函数的和公式为  （公式证明懒得写了，主要核心是利用Dirichlet卷积的性质 phi * 1 =id, mu * 1 =0(n>1) 然后利用神奇的杜教筛搞一搞 )

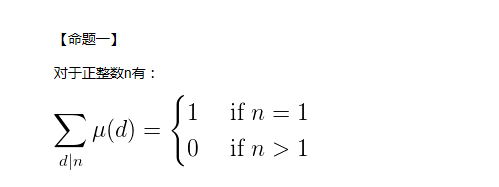因为有一个n=1的特例，所以这里有一个1，我一开始错在这里，总和答案差1........

所以我们可以预处理一波phi和mu的前缀和 然后递归的处理，用map记忆一下就可以了，复杂度为n的三分之二次幂（我不会证明）——by VANE

#include<bits/stdc++.h>
using namespace std;
const int M=5e6;
bool not_prim[M+1];
typedef long long ll;
int prim[M>>1],prim_tot;
ll mu[M+1],phi[M+1];
map<int,ll> _phi,_mu;
void pre()
{
    mu[1]=1;not_prim[1]=1;
    phi[1]=1;
    for(int i=2;i<=M;++i)
    {
        if(!not_prim[i])
        {
            prim[++prim_tot]=i;
            phi[i]=i-1;
            mu[i]=-1;
        }
        for(int j=1;j<=prim_tot&&prim[j]<=M/i;++j)
        {
            not_prim[prim[j]*i]=1;
            if(i%prim[j]==0)
            {
                phi[prim[j]*i]=phi[i]*prim[j];
                mu[prim[j]*i]=0;
                break;
            }
            phi[prim[j]*i]=phi[i]*phi[prim[j]];
            mu[prim[j]*i]=-mu[i];
        }
    }
    for(int i=1;i<=M;++i)
    {
        phi[i]+=phi[i-1];
        mu[i]+=mu[i-1];
    }
}
ll calcphi(ll n)
{
    if(n<=M) return phi[n];
    map<int,ll>::iterator it;
    if((it=_phi.find(n))!=_phi.end())
    return _phi[n];
    ll i,last;ll res=1ll*n*(n+1)/2;
    for(i=2;i<=n;i=last+1)
    {
        last=n/(n/i);
        res-=(last-i+1)*calcphi(n/i);
    }
    return _phi[n]=res;
}
ll calcmu(ll n)
{
    if(n<=M) return mu[n];
    map<int,ll>::iterator it;
    if((it=_mu.find(n))!=_mu.end()) return _mu[n];
    ll i,last;ll res=1;
    for(i=2;i<=n;i=last+1)
    {
        last=n/(n/i);
        res-=(last-i+1)*calcmu(n/i);
     } 
     return _mu[n]=res;
}
int main()
{
    pre();
    int t;
    scanf("%d",&t);
    while(t--)
    {
        ll n;
        scanf("%lld",&n);
        printf("%lld %lld
",calcphi(n),calcmu(n));
    } 
}