傻子代码行列式

By:大奕哥

今天给大家介绍行列式

引入两个概念 排列和逆序

排列即为一个序列，逆序为i<j&&a[i]>a[j]的个数记为r（a[1],a[2]...a[n]）

然后我们对于一个n^n的行列式，他的值就是Σ（-1）^r(j1,j2,j3...jn)*a[1][j1]*a[2][j2]*...*a[n][jn].此时j互不相等

由上面可以看出共有n！个数相加。

下面介绍行列式的几个性质

1.转置不改变行列式的值

转置：第i行变成第i列，相当于将行列式旋转九十度。

2.行（列）的公因子可以提出来

3.行列式具有可加性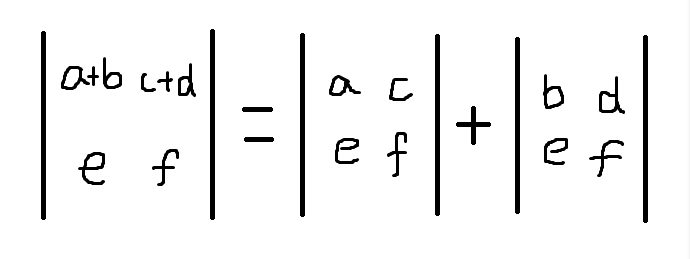

4.行列式中如果某两行（列）对应位置成比例行列式的值为0

5.行列式中任意两行调换顺序行列式值为相反数

*6.行列式中某行（列）的倍数加到另外一行（列）上时行列式的值不变

下面再介绍两个概念

余子式和代数余子式

余子式：拿掉任意一个含有a[i][j]的行和列后剩下的n-1阶的行列式为a[i][j]的余子式,值为det(a[i][j])。

代数余子式：M(i,j)=(-1)^(i+j)*det(a[i][j])。

对于行列式我们必须要认清一个概念就是虽然它看上去是矩阵但他实际上表现得是一个数值。

例如一个三阶的行列式我们可以抽象看成是三条向量的面相交所成的几何模型的体积。

下面给出行列式的通项

det(A)={

               a[1][1]   (n=1)

　　　    ∑(-1)^(i+j)*a[1][j]*det(A[1][j]) (j=1.....n) (n>1)

　　　  }

行列式的值还可以展开为det(A)=∑a[i][1]*M(i,1)  (i=1.....n)=∑a[1][i]*M(1,i)  (i=1.....n)。

如果我们稍作修改就可以得到另外一个式子∑a[i][j]*M(i,j)  (i=1.....n&&i!=j)=∑a[j][i]*M(j,i)  (i=1.....n&&i!=j)=0。

想必读者看到这里可以轻易想出递归求行列式值得方法，但仔细一想复杂度达到了惊人的n!

#include<bits/stdc++.h>
using namespace std;
int n,m,a[15][15],d[15];
typedef long long ll;
ll work(int y,int k)
{
    if(k==1)return 1;
    int b[15][15];
    memcpy(b,a,sizeof(b));memset(a,0,sizeof(a));
    int cnt;ll ans=0;
    for(int i=2;i<=k;++i)
    for(int j=1,cnt=1;j<=k;++j,++cnt)
    {
        if(j==y){cnt--;continue;}
        a[i-1][cnt]=b[i][j];
    }
    for(int i=1;i<k;++i){int flag=(1+i)%2?-1:1;ans+=1ll*flag*a[1][i]*work(i,k-1);}
    memcpy(a,b,sizeof(a));
    return ans;
}
int main()
{
    scanf("%d",&n);ll ans=0;
    for(int i=1;i<=n;++i)
    for(int j=1;j<=n;++j)
    scanf("%d",&a[i][j]);
    for(int i=1;i<=n;++i){int flag=(1+i)%2?-1:1;ans+=1ll*flag*a[1][i]*work(i,n);}
    printf("%lld
",ans);
    return 0;
}

下面给出一个非常有利于我们求行列式值的方法

在行列式中我们把左上到右下连线，如果在这条直线两边存在一边的值都为0，则答案为a[1][1]*a[2][2]*......*a[n][n]

那么如果是右上和左下连边呢，结果就是上面答案*(-1)^((n-1)*n/2)

看到这里就可以用我们的高斯消元求解行列式的值了复杂度是O（n^3）

#include<bits/stdc++.h>
using namespace std;
double ans=1,a[15][15];
int n;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;++i)
    for(int j=1;j<=n;++j)
    scanf("%lf",&a[i][j]);
    for(int i=1;i<n;++i)
    {
        for(int j=i+1;j<=n;++j)
        {
            if(a[j][i])
            {
                double d=a[i][i]?a[j][i]/a[i][i]:0;
                for(int k=i;k<=n;++k)
                {
                    a[j][k]-=a[i][k]*d;
                }
            }
        }
    }
    for(int i=1;i<=n;++i)ans=ans*a[i][i];
    printf("%lf",ans);
    return 0;
}

 18.1.4修改

在做题的过程中我遇到了对答案取模的运算，所以double在这里就不行了，我们要使用辗转相减的高斯消元复杂度加了一个log

注意交换时答案会变为原来的相反数。

#include<bits/stdc++.h>
using namespace std;
int a[50][50];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)scanf("%d",&a[i][j]);
    long long ans=1;
    for(int i=1;i<=n;++i)
    {
        for(int j=i+1;j<=n;++j)
        while(a[j][i])
        {
            long long t=a[i][i]/a[j][i];
            for(int k=i;k<=n;++k) a[i][k]-=a[j][k]*t;
            for(int k=i;k<=n;++k) swap(a[i][k],a[j][k]);
            ans=-ans;
        }
        ans=ans*a[i][i];
    }
    cout<<ans<<endl;
    return 0; 
}

 我们对于矩阵的学习还可以与行列式结合在一起

大家可以阅读这份资料

https://max.book118.com/html/2016/0130/34392001.shtm

我们在这里只给出求解逆矩阵的方法，采用初等变换，复杂度仍是高斯消元

    for(ll i=1;i<=n;++i)Ax[i][i]=1;
    for(int i=1;i<=n;++i)
    {
        for(int j=i;j<=n;++j)
        if(A[j][i])
        {
            for(int k=1;k<=n;++k)
            {
                swap(Ax[i][k],Ax[j][k]);
                swap(A[i][k],A[j][k]);
            }
            break;
        }
        ll x=qmod(A[i][i],mod-2);
        
        for(int j=i+1;j<=n;++j)
        {
            ll tmp=A[j][i]*x%mod;
            for(int k=1;k<=n;++k)
            {    
                A[j][k]=(A[j][k]-A[i][k]*tmp%mod+mod)%mod;
                Ax[j][k]=(Ax[j][k]-Ax[i][k]*tmp%mod+mod)%mod;
            }
        }
        for(int k=1;k<=n;++k)
        {
            A[i][k]=A[i][k]*x%mod;
            Ax[i][k]=Ax[i][k]*x%mod;
        }
    }
    for(int i=1;i<=n;++i)
    {
        for(int j=i+1;j<=n;++j)
        {
            if(A[i][j])
            {
                ll tmp=A[i][j];
                for(int k=1;k<=n;++k)
                {
                    A[i][k]=(A[i][k]-A[j][k]*tmp%mod+mod)%mod;
                    Ax[i][k]=(Ax[i][k]-Ax[j][k]*tmp%mod+mod)%mod;
                }
            }
        }
    }
    for(ll i=1;i<=n;++i)for(ll j=1;j<=n;++j)Ax[i][j]=Ax[i][j]*det%mod;
    for(ll i=1;i<=n;++i)for(ll j=1;j<=i;++j)swap(Ax[i][j],Ax[j][i]);