梯度下降算法在神经网络的训练中扮演着非常重要的角色,在本文中,我们来仔细介绍一下梯度下降算法。假设我们遇到了一个函数,其方程为F(x)=x2+10x+5,现在我们要去求它的最值(最大值或者最小值),如果让我们自己来求,我们可以很容易看出该函数存在最小值,并且在对称轴x=-b/2a=-5处取得最小值,最小值为-20。但是如果让计算机去求它的最小值应该怎样做呢?这就是我们今天要介绍的内容。
我们画出该方程的图像,如图1-2所示:
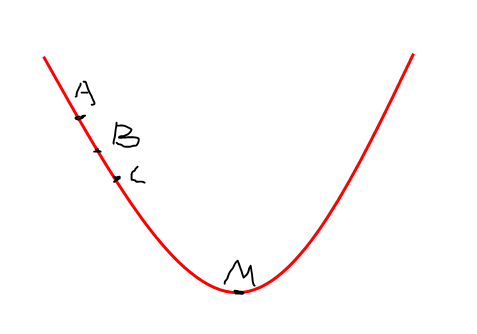
图1-2 函数F(x)=x2+10x+5的图像
从图中可以看出,函数的最小值就是M点处,但是计算机应该怎样找到M点,首先我们在该图上随便找一点,该点为A点,然后沿着A点,往下走一步,此时就到了B点,紧接着再往下走一点,就回到达C点,就这样一步一步地走,总会到达我们要找的最小值点,也就是M点。可能这时候有人会问,在找到A点后,我们怎么能够判断往哪边走是向下走?如果往A的左边走一直就会向上,这样永远就走不到M点了啊,此时我们需要考虑一下,怎样才能保证每一步都是在向下走呢?这时候就轮到你在学校时天天抱怨学了没用的导数起作用了,可能有人疑惑,导数在这里有什么用呢,那让我们回忆一下导数的几何意义,导数就是图像在该点处切线的斜率,也就是函数值上升的方向。等等,上升的方向?那么给它添负号不就变成了函数值下降的方向,没错函数的导数,也称为梯度,加负号就是函数值下降的方向。方向问题解决了,但还有一个问题,每次向下走一步,这一步到底是多大,在这里我们会用一个常数a来表示这一步的大小,a被称为学习率,是人为给定的,这个值不能太大也不能太小,太大了容易跨过最小值M,太小了向下走次数太多,不容易在短时间内找到M点。我们怎样知道要找的M是否已经找到呢?当然是当该点的导数是否为0来决定,下面我们简述一下梯度下降算法:
1.随便取一个值x0。
2.判断函数在x0处的导数是否为0。
3.如果为0,函数的最小值点就是x0,如果不等于0,x0=x0-a*F1(x0)返回第2步。
接下来我们使用程序来实现:
public class Gradient { public static void main(String[] args) { float x0 = 1.0f; //学习率 float a = 0.3f; int i=0; while (true) { //求函数F(x)=x2+10x+5在x0处的导数 float g=2*x0+10; System.out.println("第"+i+"次的导数(梯度)为"+g); //一般不能精确到0,足够小即可认为等于0 if (Math.abs(g)<0.001) { break; } x0=(x0-a*g); i++; } System.out.println("函数的最小值点为"+x0+",最小值为"+(x0*x0+10*x0+5)); } }
程序运行结果如下:
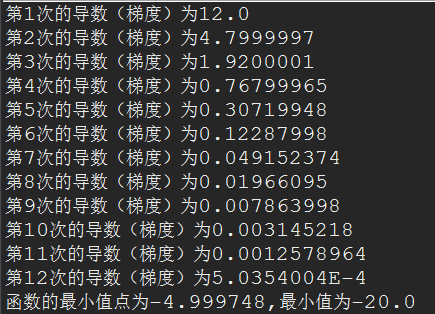
从图中我们可以看到程序运行的结果很接近最小值点-5和最小值-20,随着迭代次数的增加,结果会越来越准确。