算法的空间复杂度

续上节《--算法的时间复杂度--》https://www.cnblogs.com/nbk-zyc/p/12293186.html

1 算法的时间复杂度

　　常见算法的时间复杂度

              

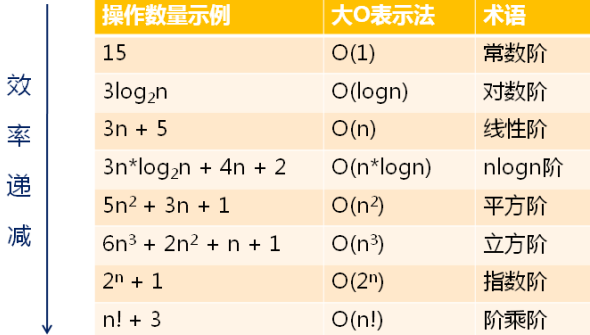
　　常见算法的时间复杂度比较：

             

　　时间复杂度的案例分析：

#include <iostream>

using namespace std;

/**
 * 功能： 查找数组下标并返回
 * 参数：
 *  a[]： 输入数据
 *  n：数组长度 
 *  v：待查找的元素
 * 返回值：待查找元素的数组下标
*/
int find(int a[], int n, int v)
{
    int ret = -1;

    for(int i = 0; i < n; i++)  // O(n)
    {
        if( a[i] == v)
        {
            ret = i;
            break;
        }
    }

    return ret;
}



int main(int argc, char* argv[])
{
    int arr[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
    int length = sizeof(arr)/sizeof(int);
    int min = find(arr, length, 1);     // 最好情况，算法执行1次，O(1)
    int max = find(arr, length, 10);    // 最差情况，算法执行10次，O(10)

    return 0;
}

　　结论：一般来说，算法的时间复杂度需要考虑其最坏的情况，因为只有这样，才能满足其最好情况和平均情况。（上节内容都是基于算法的时间复杂度的最坏情况考虑的）

2 算法的空间复杂度（Space Complexity）

　　1） 定义：

　　　　对一个算法在运行过程中临时占用存储空间大小的度量，记作 S(n) = S(f(n)) --- 可以使用 算法的时间复杂度 来估算  算法的空间复杂度（内存分配）

　　　　　　　　n: 问题规模

　　　　　　　　f(n):空间使用函数， 与 n 有关

　　2）代码展示：

// sum1() 空间复杂度 = n+4
long sum1(int n)    // 1
{
    long ret = 0;   // 1
    int* array = new int[n];    // n
    
    for(int i=0; i<n; i++)  // 1
    {
        array[i] = i + 1;
    }
    
    for(int i=0; i<n; i++)  // 1
    {
        ret += array[i];
    }
    
    delete[] array;
    
    return ret;
}

 　  3）空间与时间的策略

　　　　1. 通常算法的时间复杂度更让人关注；

　　　　2. 如果有必要，可以通过增加额外空间来降低时间复杂度；（空间换时间） 

　　　　3. 同样，也可以通过增加算法的耗时来换取空间复杂度；（时间换空间）

/*
    问题： 
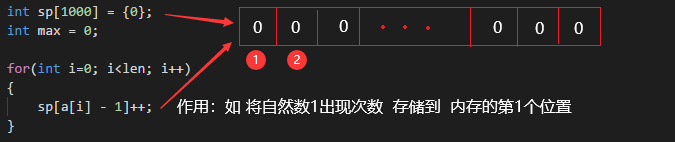
    在一个由自然数1-1000中某些数字所组成的数组中，每个数字可能出现零次或者多次。
    设计一个算法，找出出现次数最多的数字。
*/

#include <iostream>

using namespace std;

int search(int a[], int len)
{
    int sp[1000] = {0}; // 初始化每个自然数出现的次数，数组下标加1代表当前的自然数
    int max = 0;    // 保存自然数出现次数的最大值
    int ret = 0;    // 保存出现次数最多的自然数
    
    for(int i=0; i<len; i++)
    {
        sp[a[i] - 1]++; // 标记自然数的出现次数
    }
    
    for(int i=0; i<1000; i++)
    {
        if( max < sp[i] )
        {
            max = sp[i];
        }
    }
    
    for(int i=0; i<1000; i++)
    {
        if( max == sp[i] )
        {
            ret = i + 1;
            break;
        }
    }

    return ret;
}

int main(int argc, char* argv[])
{
    int a[] = {1, 1, 3, 4, 5, 6, 6, 6, 3, 3, 6};
    
    int ret = search(a, sizeof(a)/sizeof(*a));
    
    cout << ret << endl;

    return 0;
}

代码中核心思想：

　　

思考题：当两个算法的大O表示法相同时，是否意味着这两个算法效率完全相同？

　　　　答：两个算法的大O表示法相同，只代表这两个算法效率的数量级相同。

重点提示：

　　1）一般而言，工程中使用的算法，时间复杂度不超过O(n3)；

　　2）算法分析与设计时，重点考虑最坏情况下的时间复杂度；

　　3）大O表示法同样适用于算法的空间复杂度；

　　4）空间换时间是工程开发中常用的策略。