问题抛出:
程序的本质:解决实际问题的步骤描述(前提:理解实际问题)
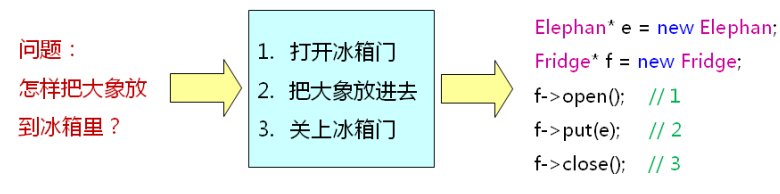
如何判断求解问题步骤的好坏
1)用尽量少的时间解决问题
2)用尽量少的步骤解决问题
3)用尽量少的内存解决问题

1 //问题:给定一个整数 n,编程求解 1 + 2 + 3 + ... + n 的和。 2 3 #include <iostream> 4 5 using namespace std; 6 7 long sum1(int n) 8 { 9 long ret = 0; 10 int* array = new int[n]; 11 12 for(int i=0; i<n; i++) 13 { 14 array[i] = i + 1; 15 } 16 17 for(int i=0; i<n; i++) 18 { 19 ret += array[i]; 20 } 21 22 delete[] array; 23 24 return ret; 25 } 26 27 long sum2(int n) 28 { 29 long ret = 0; 30 31 for(int i=1; i<=n; i++) 32 { 33 ret += i; 34 } 35 36 return ret; 37 } 38 39 long sum3(int n) 40 { 41 long ret = 0; 42 43 if( n > 0 ) 44 { 45 ret = (1 + n) * n / 2; 46 } 47 48 return ret; 49 } 50 51 int main() 52 { 53 cout << "sum1(100) = " << sum1(100) << endl; 54 cout << "sum2(100) = " << sum2(100) << endl; 55 cout << "sum3(100) = " << sum3(100) << endl; 56 57 return 0; 58 } 59 60 /* 程序效率初步分析:(详解请见后续的 事前分析估算法 ) 61 方法1-sum1(): 开辟堆空间(内存有可能申请失败),且使用了两层for循环(最差) 62 方法2-sum2():一层 for循环(一般) 63 方法3-sum3():等差数列公式,一行语句,执行效率高,不会随着项数n的增加,降低程序的执行效率;(较好) 64 */
数据结构的研究范围:解决非数值计算类型的程序问题;具体包括数据间的组织和操作方式,数据的逻辑结构和存储/物理结构。
1 数据结构中的新概念
什么是数据?---- 数据就是程序操作的对象,用于描述客观的实物。
数据的特点:1) 可以输入到计算机中;2)可以被计算机程序处理
数据的新概念:
数据元素:组成数据的基本单位
数据项:一个数据元素由多个数据项组成
数据对象:性质相同的数据元素
ps:数据 ⊇ 数据对象 ⊇ 数据元素 ⊇ 数据项

数据结构:数据对象中数据元素之间的关系。 // 如上例中,Student sArray[10]的每个元素在内存中都是线性存储的。
或者 相互之间存在特定关系的数据元素的集合;
或者 静态的描述数据元素之间的关系;
数据结构包括:逻辑结构 和 物理结构;
逻辑结构:
集合结构:数据元素之间没有特别的关系,仅同属于相同的集合中;
线性结构:数据元素之间是一对一的关系;
树形结构:数据元素之间存在一对多的层次关系;
图像结构:数据元素之间存在多对多的关系;


物理结构:逻辑结构在计算机中的存储结构;
1) 顺序存储结构:将数据存储在地址连续的存储单元中;(数组)
2) 链式存储结构:1. 将数据存储在任意的存储单元中;2.通过保存地址的方式找到相关联的数据元素;(链表)
2 初识程序的灵魂
高效的程序需要在数据结构的基础上设计和选择算法;
算法是特定问题求解步骤的描述;
对于算法而言,语言不重要,思想才重要;
算法的特性:1)2)3)4)5)基本特性 7)8)9)附加特性
1)输入:算法具有0个或多个输入;
2)输出:算法至少有1个或多个输出;
3)有穷性:算法在可接受的时间内自动结束;
4)确定性:算法中的每一步都有确定的含义,不能出现二义性;
5)可行性:算法的每一步都是可行的;
6)正确性:(基本准则)
1. 算法对于合法数据能够得到满足要求的结果;
2. 算法能够处理非法输入,并得到合理的结果;
3. 算法对于边界数据和压力数据都能得到满足要求的结果;
7)可读性:算法要求方便阅读,理解和交流;
8)键壮行:算法不应该产生莫名其妙的结果;
9)性价比:利用最少的资源得到满足要求的结果;
程序 = 数据结构 + 算法
程序的灵魂:算法
算法为了解决实际问题而存在;数据结构是算法处理问题的载体;数据结构与算法相辅相成,共同解决问题;
3 算法效率的度量方法
请思考:如果两个算法都可以同时满足功能性需求,此时在工程中最关心算法的性价比附加特性;
一般来说,算法效率的度量包括:事后统计法 与 事前分析估算法;
1)事后统计法
概念:比较不同算法对同一组输入数据的运行处理时间;
缺点:1. 为了获取不同算法的运行时间,必须编写相应的程序;
2. 运行时间严重依赖硬件 和 运行时的环境因素;
3. 算法的测试数据很难选取;
2)事前分析估算法
概念:依据统计的方法对算法效率进行估算
影响算法效率的主要因素:
1. 算法采取的策略和方法;
2. 问题的输入规模;(接下来会重点介绍)
3. 编译器所产生的代码;(如C++比JAVA生成的可执行程序执行效率高)
4. 计算机的执行速度;
使用 事前分析估算法 对数列的前n项和 进行算法效率的简单估算(累计每个算法的执行步骤) :<--查看数列的前n项和代码-->
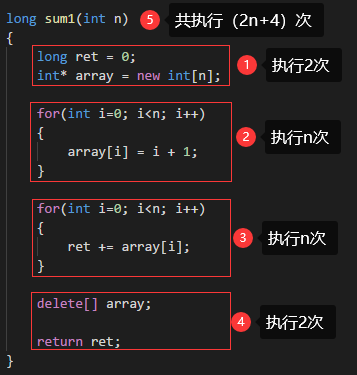
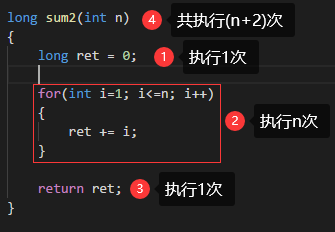

在3种求和算法种,sum1()中的关键部分的操作数量为 2n 次;sum2()中的关键部分的操作数量为 n 次;sum3()中的关键部分的操作数量为 1 次;
关键部分:除去程序的必要开销所留下的部分;
结论:随着问题的输入规模n逐渐增大,他们之间的操作数量差异也会越加明显,因此,实际算法在效率上的差异也会更加明显。
通常,对于某个算法,当问题的输入规模n增大时,他会优于另一算法,或者越来越差于另一算法。
方式1:通过可视化展示上述数列求和算法的执行效果:
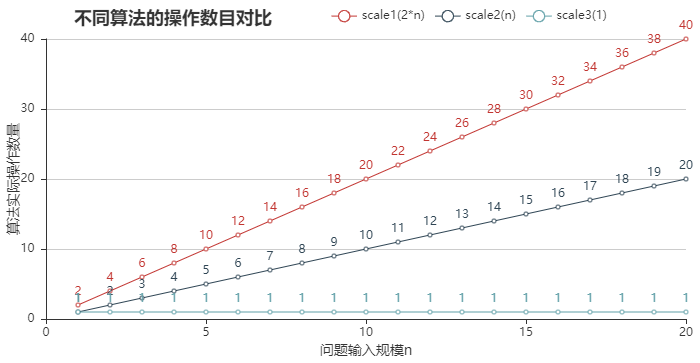

1 from pyecharts import Line 2 3 n=21 4 acount = [i for i in range(1, n)] 5 scale1 = [2*i for i in range(1, n)] 6 scale2 = [i for i in range(1, n)] 7 scale3 = [1 for i in range(1, n)] 8 9 line = Line("不同算法的操作数目对比") 10 11 line.add("scale1(2*n)", acount, scale1, xaxis_type='value') 12 line.add("scale2(n)", acount, scale2, xaxis_type='value') 13 line.add("scale3(1)", acount, scale3, xaxis_type='value', xaxis_name='问题输入规模n', yaxis_name='算法实际操作数量') 14 15 line
方式2:通过表格对比不同算法的执行效率;

结论:n == 1时,算法C( 2n2+3n+1 )和算法D( 2n3+3n+1 )的操作数量相同;当n越来越大的时候,算法C ( 2n2+3n+1 )的效率远高于算法D ( 2n3+3n+1 );

结论:判断一个算法的效率时,操作数量中的常数项和其他次要项常常可以忽略,只需要关注最高阶项就能得出结论。
