数据结构之红黑树

首先的疑问，已经有了二叉平衡树，为什么又有红黑树？（前提是要理解平衡树）

引用知乎上的回答

1. 如果插入一个node引起了树的不平衡，AVL和RB-Tree都是最多只需要2次旋转操作，即两者都是O(1)；但是在删除node引起树的不平衡时，最坏情况下，AVL需要维护从被删node到root这条路径上所有node的平衡性，因此需要旋转的量级O(logN)，而RB-Tree最多只需3次旋转，只需要O(1)的复杂度。

2. 其次，AVL的结构相较RB-Tree来说更为平衡，在插入和删除node更容易引起Tree的unbalance，因此在大量数据需要插入或者删除时，AVL需要rebalance的频率会更高。因此，RB-Tree在需要大量插入和删除node的场景下，效率更高。自然，由于AVL高度平衡，因此AVL的search效率更高。

作者：Acjx
链接：http://www.zhihu.com/question/20545708/answer/58717264

所以要明白，原由：红黑数不是严格的平衡树。红色节点是用来标记：以该节点为根节点的子树的高度要高于以该节点的兄弟节点为根节点的子树。

前提条件：

      规则1：红黑树从根节点到每个叶节点的每一条路径上的黑色节点数相等；

      规则2：如果一个节点是红色，它的父节点一定是黑色（也就是红色与红色之间是至少隔了一层的）。

因此，put操作，图片转载来自http://www.cnblogs.com/CarpenterLee/p/5503882.html

插入新节点固定为红色，因为不会改变路径上黑色节点的数目，即不违法规则1。这时需要看父节点，如果父节点为黑色，则不需要做任何额外操作。如果父节点为红色，违反规则2，需要看叔节点（父亲的兄弟节点）的颜色，图为父节点在祖父节点的左侧，分为两种情况：a)如果叔节点为红色，如图情况一；b)叔节点为黑色，x节点在父节点的右侧，如图情况二;c))叔节点为黑色，x节点在父节点的左侧，如图情况三。另外的三种情况是对称的，即，父节点在祖父节点的右侧。

需要注意，代码中合并了b,c两种情况，如果没有b情况，直接执行c情况，如果有b情况，先b,后c。

//红黑树调整函数fixAfterInsertion()
private void fixAfterInsertion(Entry<K,V> x) {/
    x.color = RED;
    while (x != null && x != root && x.parent.color == RED) {//注意while循环条件，和循环后的语句
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
            Entry<K,V> y = rightOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {//如果y为null，则视为BLACK
                setColor(parentOf(x), BLACK);              // 情况1
                setColor(y, BLACK);                        // 情况1
                setColor(parentOf(parentOf(x)), RED);      // 情况1
                x = parentOf(parentOf(x));                 // 情况1
            } else {
                if (x == rightOf(parentOf(x))) {
                    x = parentOf(x);                       // 情况2，叔节点为黑色，x节点在父节点的右侧，其实就是LR旋转，还是直接进入情况3，就RR旋转
                    rotateLeft(x);                         // 情况2
                }
                setColor(parentOf(x), BLACK);              // 情况3，叔节点为黑色，x节点在父节点的左侧， RR旋转
                setColor(parentOf(parentOf(x)), RED);      // 情况3
                rotateRight(parentOf(parentOf(x)));        // 情况3
            }
        } else {
            Entry<K,V> y = leftOf(parentOf(parentOf(x)));
            if (colorOf(y) == RED) {
                setColor(parentOf(x), BLACK);              // 情况4
                setColor(y, BLACK);                        // 情况4
                setColor(parentOf(parentOf(x)), RED);      // 情况4
                x = parentOf(parentOf(x));                 // 情况4
            } else {
                if (x == leftOf(parentOf(x))) {
                    x = parentOf(x);                       // 情况5
                    rotateRight(x);                        // 情况5
                }
                setColor(parentOf(x), BLACK);              // 情况6
                setColor(parentOf(parentOf(x)), RED);      // 情况6
                rotateLeft(parentOf(parentOf(x)));         // 情况6
            }
        }
    }
    root.color = BLACK;
}
　　伪代码：
　　

x: 当前节点
p: x的父节点
pp: p的父节点
y: p的兄弟结点

whie x!=null && p == red && x != root
　　if p 是 pp的左孩子
　　　　if y是红色
　　　　　　set p=黑色
　　　　　　set y=黑色
　　　　　　set pp = 红色
　　　　　　令 x =pp
　　　　else
　　　　　　if x是p的右孩子 {
　　　　　　　　令 x = p
　　　　　　　　rotateLeft(p) }
　　　　　　set p = 黑色
　　　　　　set pp = 红色
　　　　　　rotateRight(pp)

　　else p是pp的右孩子
　　　　if y是红色
　　　　　　set p=黑色
　　　　　　set y=黑色
　　　　　　set pp = 红色
　　　　　　令 x =pp
　　　　else
　　　　　　if x是p的左孩子 {
　　　　　　　　令 x = p
　　　　　　　　rotateRight(p) }
　　　　　　set p = 黑色
　　　　　　set pp = 红色
　　　　　　rotateLeft(pp)

删除节点，参考http://www.cnblogs.com/CarpenterLee/p/5525688.html

如果P节点至少有一个孩子节点，寻找后继节点，用后继节点替换当前结点，调整后继节点。

如果P节点没有孩子节点，直接调整p节点。

如果删除的是红色节点，不需要任何操作，

如果删除的黑色节点，

如图：

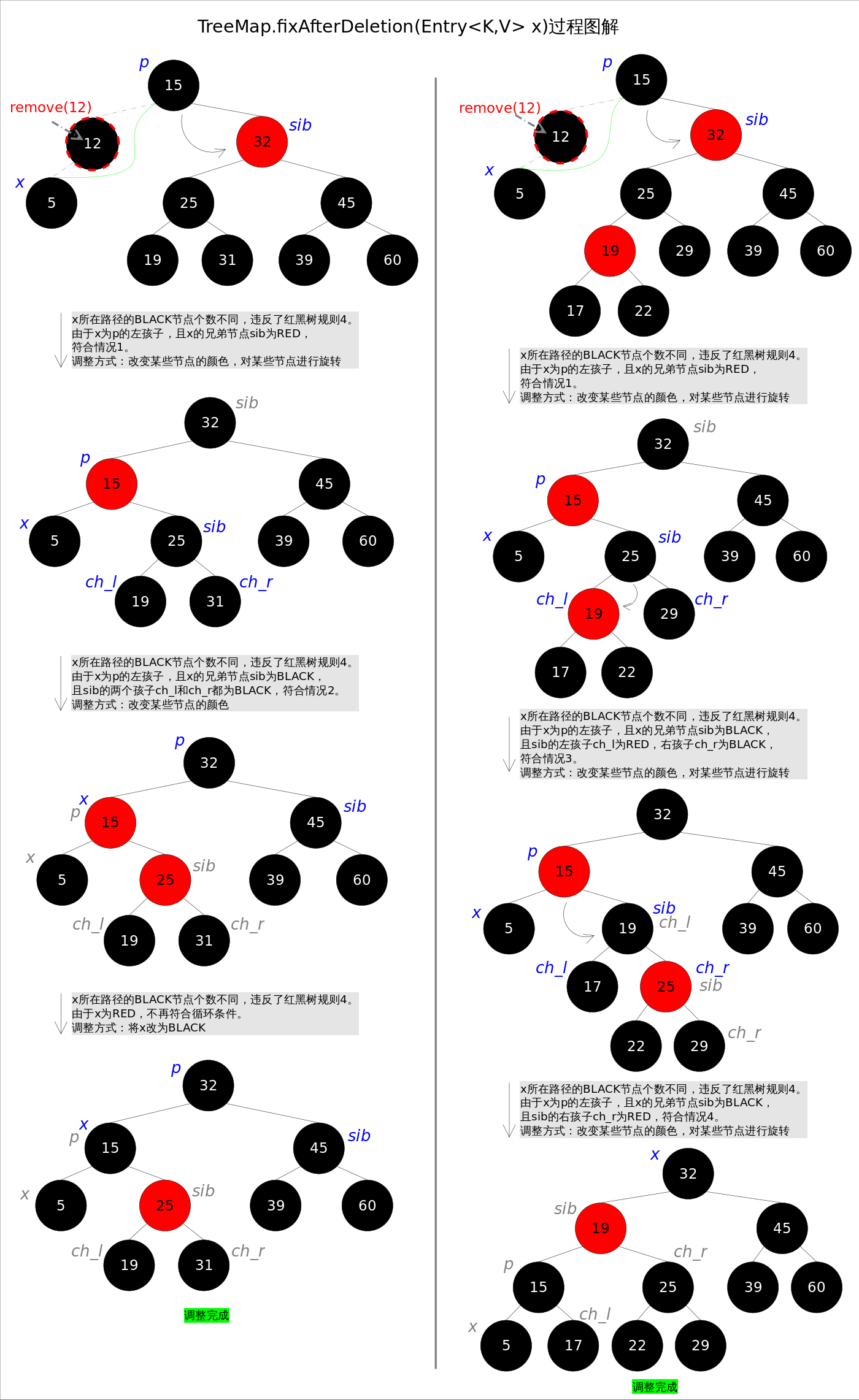
// 红黑树entry删除函数deleteEntry()
private void deleteEntry(Entry<K,V> p) {
    modCount++;
    size--;
    if (p.left != null && p.right != null) {// 2. 删除点p的左右子树都非空。
        Entry<K,V> s = successor(p);// 后继
        p.key = s.key;
        p.value = s.value;
        p = s;//这时候p指向了后继结点S，继续向下执行
    }
    Entry<K,V> replacement = (p.left != null ? p.left : p.right);
    if (replacement != null) {// 1. 删除点p只有一棵子树非空。顶替P
        replacement.parent = p.parent;
        if (p.parent == null)
            root = replacement;
        else if (p == p.parent.left)
            p.parent.left  = replacement;
        else
            p.parent.right = replacement;
        p.left = p.right = p.parent = null;
        if (p.color == BLACK)
            fixAfterDeletion(replacement);// 调整
    } else if (p.parent == null) {
        root = null;
    } else { // 1. 删除点p的左右子树都为空，可以调整并直接删除
        if (p.color == BLACK)
            fixAfterDeletion(p);// 调整
        if (p.parent != null) {
            if (p == p.parent.left)
                p.parent.left = null;
            else if (p == p.parent.right)
                p.parent.right = null;
            p.parent = null;
        }
    }
}

//观点就是少了一个黑色节点要补回来
private void fixAfterDeletion(Entry<K,V> x) {//注意while循环条件，和循环后的语句
    while (x != root && colorOf(x) == BLACK) {
        if (x == leftOf(parentOf(x))) {
            Entry<K,V> sib = rightOf(parentOf(x));
            if (colorOf(sib) == RED) {//步骤一
                setColor(sib, BLACK);                   // 情况1，被删除的节点p,的原兄弟节点sib为红色，
                setColor(parentOf(x), RED);             // 情况1
                rotateLeft(parentOf(x));                // 情况1
                sib = rightOf(parentOf(x));             // 注意此时，sib变了。
            }
            if (colorOf(leftOf(sib))  == BLACK &&      //步骤二，分两种，sib节点的孩子节点全部为黑色
                colorOf(rightOf(sib)) == BLACK) {
                setColor(sib, RED);                     // 情况2
                x = parentOf(x);                        // 情况2
            } else {                                   //sib的孩子节点有一个是红色，看红色是在左边则，RL旋转，如果右边，则进入情况四，直接LL旋转
                if (colorOf(rightOf(sib)) == BLACK) {
                    setColor(leftOf(sib), BLACK);       // 情况3
                    setColor(sib, RED);                 // 情况3
                    rotateRight(sib);                   // 情况3
                    sib = rightOf(parentOf(x));         // 情况3
                }
                setColor(sib, colorOf(parentOf(x)));    // 情况4，直接LL旋转
                setColor(parentOf(x), BLACK);           // 情况4
                setColor(rightOf(sib), BLACK);          // 情况4
                rotateLeft(parentOf(x));                // 情况4
                x = root;                               // 情况4
            }
        } else { // 跟前四种情况对称
            Entry<K,V> sib = leftOf(parentOf(x));
            if (colorOf(sib) == RED) {
                setColor(sib, BLACK);                   // 情况5
                setColor(parentOf(x), RED);             // 情况5
                rotateRight(parentOf(x));               // 情况5
                sib = leftOf(parentOf(x));              // 情况5
            }
            if (colorOf(rightOf(sib)) == BLACK &&
                colorOf(leftOf(sib)) == BLACK) {
                setColor(sib, RED);                     // 情况6
                x = parentOf(x);                        // 情况6
            } else {
                if (colorOf(leftOf(sib)) == BLACK) {
                    setColor(rightOf(sib), BLACK);      // 情况7
                    setColor(sib, RED);                 // 情况7
                    rotateLeft(sib);                    // 情况7
                    sib = leftOf(parentOf(x));          // 情况7
                }
                setColor(sib, colorOf(parentOf(x)));    // 情况8
                setColor(parentOf(x), BLACK);           // 情况8
                setColor(leftOf(sib), BLACK);           // 情况8
                rotateRight(parentOf(x));               // 情况8
                x = root;                               // 情况8
            }
        }
    }
    setColor(x, BLACK);
}