首先,什么叫做左递归呢? 一个左递归的语法通常有这样的形式 : A-> Aa .而自顶向下的语法分析是无法处理左递归语法的。为什么呢?无论是递归分析还是预测分析或者是LL文法分析,在碰到左递归这种语法时都会陷入死循环当中。如果我们用递归分析,那么在分析A这个非终结符号的时候就会调用functionA,functionA将A分解成A,a,然后在我们再次碰到A的时候又会调用functionA,这样便形成了无限递归。如果我们用非递归的LL文法分析,那么在我们将把A->Aa无限次地压入到栈中,即每次弹出A都会压入Aa。所以我们必须采取手段消除左递归,下面给出标准方法。
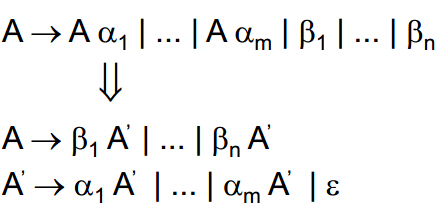 其中β1...βn 不是从A开始
其中β1...βn 不是从A开始
其实原理在于通过转换将A的语法不从非终结符号(A本身)开始,而是从终结符号β1...βn 开始。虽然A的原语法是从A本身开始的,但是第一个符号一定是β1...βn中的一个,而不可能是任何一个α。所以我们通过一个中间变量A'来表示剩下的α,然而不要忘记由于A' ->αA' 这条规则,A' -> ε 必须也存在于语法规则中,否则末尾将无法匹配完成。
但是,上述方法只适用于立即左递归,还有一种更隐蔽的非立即左递归,如 S -> Aa | b , A -> Sc | d ,我们如果用自顶向下的分析方法会陷入 S -> Aa -> Sca 这样的死循环中。当然,也有相应的解决办法。
将所有非终端符号以某个固定的顺序 排列
排列
- 从 i = 1 到 n {
- 从 j = 1 到 i – 1 {
-
- 设
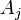 的生成规则为
的生成规则为
- 设
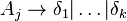
- 将所有规则
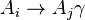 换成
换成
- 将所有规则
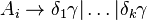
- 移除
 规则中的直接左递归
规则中的直接左递归
- 移除
-
- }
- 从 j = 1 到 i – 1 {
- }
也许看上面的规则过于抽象,我们用S -> Aa | b , A -> Sc | d 来实践一下上述的方法。我们以S,A的顺序排列。则只需执行一次主程序体,且Ai 为A,Aj为S。则:- A -> Aac | bc | d, 然后再运用前面的规则消除直接左递归可得:A -> bcA' | dA' , A' -> acA' | ε
- 请注意,以上的解决方案是基于右递归的文法,并不是完全适用于所有的情况。我们得到的文法可能含有 ε表达式,并且可能会改变语法的结合律。解决方案就是保留左递归的语法,不用自顶向下的方式分析。