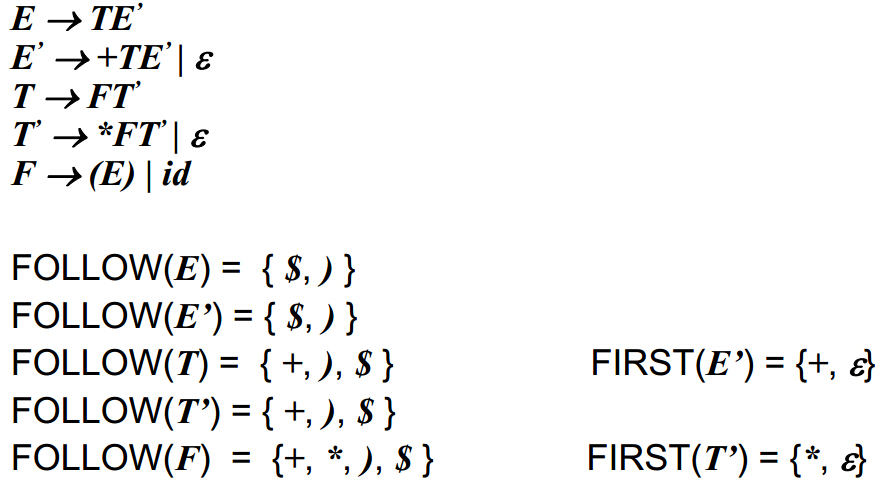在我们得到了Context-free grammar 之后,下一步就要将它转换成一棵语法分析树了,语法分析树使得我们的编译器能够识别输入串是否符合我们的Context-free grammar(中文翻译为上下文无关语言)
有两种方法能够将Context-free grammar转换为语法分析树。今天我们只介绍自顶向下的方法。
自顶向下的语法分析是从根节点开始,深度优先地创建语法分析树的各个节点。有递归向下分析和预测分析两大类方法。
递归向下分析
递归向下的语法分析可能需要回溯(aka需要重复扫描输入),考虑以下文法: S -> aBc ,B -> bc | b ,当我们用递归向下分析,输入为abc时,语法树如下图:

当我们第一次匹配时识别失败了(a匹配a,bc匹配B,最后一个c未匹配到),输入必须回到b,用B的另外一种方式匹配。
递归向下的分析十分直观,实现起来也比较方便,但效率较低,所以一般不采用。递归向下的分析方法实际上是深度优先搜索+回溯。而下面要说的预测分析则是用高效的动态规划来实现语法分析。
递归预测向下分析
在讨论使用动态规划的预测向下分析之前,我们先来看一种特殊的预测向下分析。它在本质上也是递归的,唯一的区别在于它不需要回溯。考虑以下文法:A -> aBb | bAB,伪代码实现如下:
proc A {
case 当前标记 {
‘a’:匹配a, 移动到下个标记;
调用函数B;
匹配b, 移动到下个标记;
‘b’:匹配b,移动到下个标记;
调用函数A;
调用函数B;
}
}
其实这种分析方式与前者的区别就在于它用了case语句来预测A的两种可能性,从而做出不同的判断。但这种方式的效率也是不如动态规划的。
非递归预测向下分析
非递归预测向下分析是表驱动的分析方法,也叫做LL(1)分析。第一个"L"表示从左到右扫描。第二个"L"表示产生最左推导。"1"表示每次只要往前走一步就可以决定语法分析的动作。
所谓表驱动就是通过查表的方式来分析一个输入流是否符合文法。假设我们已经得到了这张语法分析表,现在来具体分析这种方式是如何工作的。
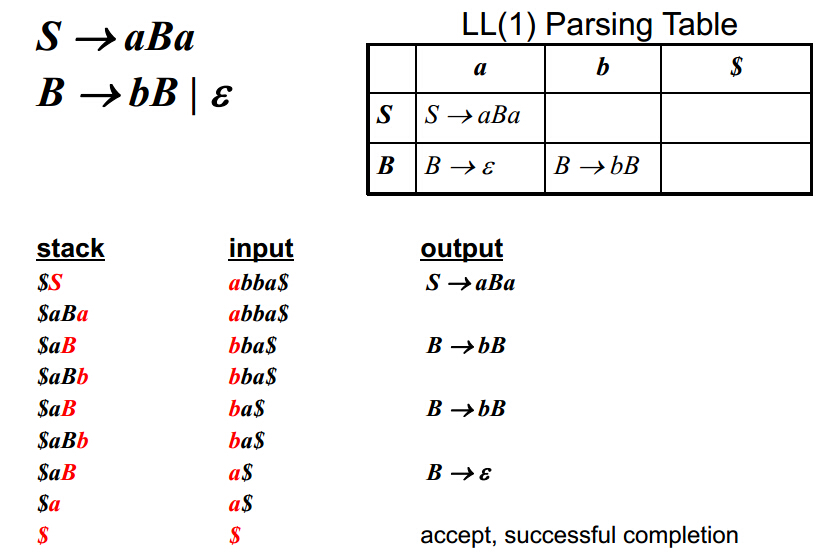
首先我们需要一个栈来存储start symbol,即语法树的根。然后从表中查找当栈顶为S,输入为a时对应的文法,然后将S替换为aBa(注意入栈顺序),然后a与输入的a匹配,非终结标志B对应到了b,此时查找表中相应的文法,将B弹出栈,将bB压入栈(注意顺序)。以此类推直到栈底的终止字符匹配到了输入的终止字符,表示匹配成功。
上面是实例,下面我们给出一个高度的分析行为概括:
当栈顶为X,当前输入为a时,有以下四种分析行为:
1.如果X和a都为终止符号$,匹配成功,停止匹配。
2.如果X和a都是同一种终结标志(terminal symbol),将X弹出栈,将输入移动到下个标志。(表示该标志成功匹配,准备匹配下个标志)
3.如果X是非终结标志(nonterminal symbol),查询语法分析表,找到[S,a],如果[S,a]为 X->Y1Y2Y3...Yk,则将Y1Y2Y3...Yk逆序放入栈中。(即Y1为栈顶)
4.不符合以上三种情况,匹配失败,进入错误恢复模式。
可以看到,有了这张语法分析表之后分析起来非常的方便。那么我们如何构建这张语法分析表呢?
首先我们需要用到两个函数first(a),follow(A),下面详细解释两个函数的含义以及如何计算他们。
first(a) : 可以从a推导得到的串的首符号(终结符号)的合集。
计算规则如下:
1.如果X是终结符号,first(X)={X}
2.如果X是非终结符号且X->ε是一个文法规则,那么ε属于first(X)
3.如果X是非终结符号且X->Y1Y2Y3...Yn是一个文法规则,那么:①如果终结符号a在first(Yi)中且ε在所有的first(Yj) (j-1,2,...i-1)中,那么a也属于first(X) ②如果ε在所有的first(Yj) (j=1,2...n) 那么ε也属于first(X)
4.如果X本身为ε,那么first(X)={ε}
以上的规则将一直使用直到没有元素能够加入到任何first()当中。
follow(A):从A之后可以立即得到(可以理解为与A相邻)的终结符号的集合,其中A是非终结符号。
计算规则如下:
1.如果A->aBb是一个文法规则,那么所有在first(b)中的元素除了ε都包含在follow(B)中。
2.如果A->aB是一个文法规则或者A->aBb是一个文法规则且ε包含在first(b)中,那么在follow(A)中的所有元素都在follow(B)中。即follow(A)属于follow(B)
以上的规则也将一直使用直到没有元素能够加入到任何follow()当中。
下面给出两个实例让读者自行思考。
接下来让我们使用这两个函数来完成语法分析表构建的算法。
对于在语法合集G中的每条语法 ,(以A->a来表示):
for 每个终结符号 p in first(a):
将A->a 加入到表中的M[A,p]
if ε in first(a)
for 每个follow(A)中的终结符号p:
将A->a 加入到M[A,p]
if ε in first(a) 并且 $ 属于follow(A):
将A->a 加入到M[A,$]
当然并不是所有的语法规则都是LL文法的,也就是说有可能出现在一个表中的某行某列存在多个文法规则,比如下图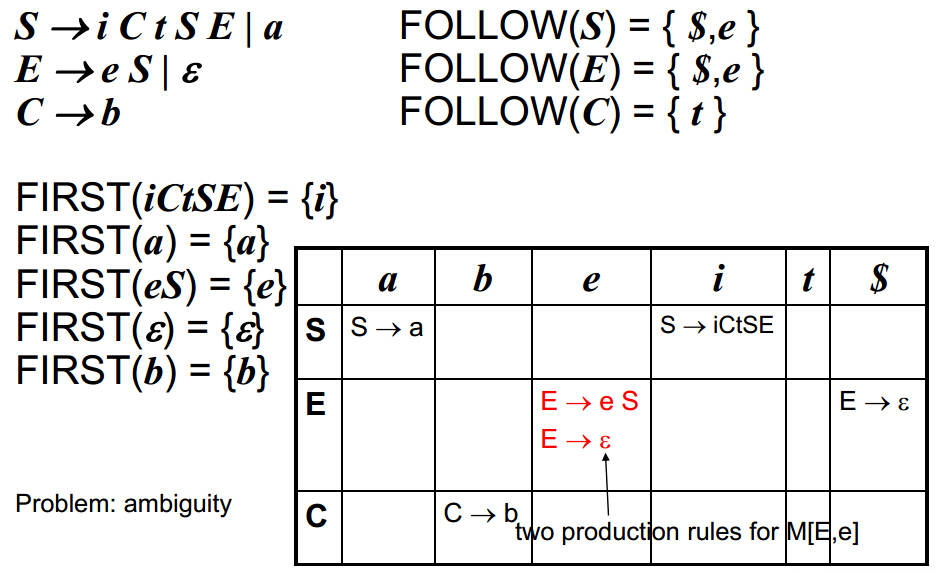
在M[E,e]中出现了两个文法规则使得语法分析产生了二义性(ambiguity)。可以看出LL文法并不是万能的。那么如果我们碰到了这样的情况应该怎么办呢?
首先我们可以先将存在左递归的文法消除成非左递归的文法。其次我们还可以提取左公因子,如果这样处理之后还是不行的话那么说明这个语法本身就存在二义性或者它天生就不是LL文法。