11月22日天梯训练补题报告

7-4 倒数第N个字符串 (15分)

 

给定一个完全由小写英文字母组成的字符串等差递增序列，该序列中的每个字符串的长度固定为 L，从 L 个 a 开始，以 1 为步长递增。例如当 L 为 3 时，序列为 { aaa, aab, aac, ..., aaz, aba, abb, ..., abz, ..., zzz }。这个序列的倒数第27个字符串就是 zyz。对于任意给定的 L，本题要求你给出对应序列倒数第 N 个字符串。

输入格式：

输入在一行中给出两个正整数 L（2 $10^5$

输出格式：

在一行中输出对应序列倒数第 N 个字符串。题目保证这个字符串是存在的。

输入样例：

3 7417

 

输出样例：

pat
题解：26个字母一循环，其实就是26进制的应用，每一位的数字对应一个字母；
要注意的是：倒数第1个其实是第0个，要将m-1!!!
ac代码：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<map>
using namespace std;
int main(){
    int l,m,i,a[9]={0},k;
    cin>>l>>m;
    int mm=m-1;
    for(i=0;i<l;i++){
        if(mm%26<=26){
            a[i]=mm%26;
            mm=mm/26;
        }
        if(mm==0){
            k=i;
            break;
        }
    }
    for(i=l-1;i>=0;i--){            
            cout<<char('z'-a[i]);
    }
    cout<<endl;
} 

7-5 整除光棍 (20分)

 

这里所谓的“光棍”，并不是指单身汪啦~ 说的是全部由1组成的数字，比如1、11、111、1111等。传说任何一个光棍都能被一个不以5结尾的奇数整除。比如，111111就可以被13整除。 现在，你的程序要读入一个整数x，这个整数一定是奇数并且不以5结尾。然后，经过计算，输出两个数字：第一个数字s，表示x乘以s是一个光棍，第二个数字n是这个光棍的位数。这样的解当然不是唯一的,题目要求你输出最小的解。

提示：一个显然的办法是逐渐增加光棍的位数，直到可以整除x为止。但难点在于，s可能是个非常大的数 —— 比如，程序输入31，那么就输出3584229390681和15，因为31乘以3584229390681的结果是111111111111111，一共15个1。

输入格式：

输入在一行中给出一个不以5结尾的正奇数x（<1000）。

输出格式：

在一行中输出相应的最小的s和n，其间以1个空格分隔。

输入样例：

31

 

输出样例：

3584229390681 15

题解：模拟除法运算过程，从第一位开始除x，将余数补到下一位，直至余数为0为止，
注意：首位为0不输出，要对此进行细节处理。
ac代码：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<map>
using namespace std;
int main(){
    int x,i,s=1,k=0;
    cin>>x;
    for(i=1;;i++){
        if(s/x!=0){
            k=1;
        }
        if(k){
            cout<<s/x;
        }
        s=s%x;
        if(s==0){
            cout<<" "<<i<<endl;
            break;
        }
        s=s*10+1;    
    }
    return 0;
} 

7-12 列车调度 (25分)

 

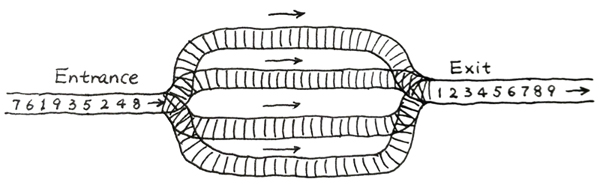
火车站的列车调度铁轨的结构如下图所示。

两端分别是一条入口（Entrance）轨道和一条出口（Exit）轨道，它们之间有N条平行的轨道。每趟列车从入口可以选择任意一条轨道进入，最后从出口离开。在图中有9趟列车，在入口处按照{8，4，2，5，3，9，1，6，7}的顺序排队等待进入。如果要求它们必须按序号递减的顺序从出口离开，则至少需要多少条平行铁轨用于调度？

输入格式：

输入第一行给出一个整数N (2 ≤ N ≤10^5)，下一行给出从1到N的整数序号的一个重排列。数字间以空格分隔。

输出格式：

在一行中输出可以将输入的列车按序号递减的顺序调离所需要的最少的铁轨条数。

输入样例：

9
8 4 2 5 3 9 1 6 7

 

输出样例：

4
题解：
ac代码：

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<map>
using namespace std;
int main(){
    int n,a[100005];
    cin>>n;
    int k;
    int m=0;
    while(n--){
        cin>>k;
        if(m==0||a[m-1]<k){
            a[m++]=k;
        }
        else{
            int l=0;
            int r=m-1;
            while(l<r){
                int mid=l+(r-l)/2;
                if(a[mid]>k){
                    r=mid-1;
                }  
                else{
                    l=mid+1;    
                }
            }
            a[l]=k;
        }
    }
    cout<<m<<endl;
    return 0;
}